A fringe tracking unit is needed in order to reduce the OPD variations, either
systematic or random, to a fraction of the coherence length. The delay line is
permanently adjusted for this purpose, and its motion is controlled by the error
signal of the tracking unit. Simultaneous observations in at least two different
wavebands are needed. Let ![]() and
and ![]() the mean wavenumbers of the
two bands, that we call guiding wavenumbers . The phase difference is, with (17) and :
the mean wavenumbers of the
two bands, that we call guiding wavenumbers . The phase difference is, with (17) and :
| (19) |
Maintaining zero phase difference whatever the delay length gives the condition for zero group
delay tracking at ![]() :
:
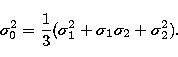 |
(20) |
The two observed bands should be large enough for sensitivity purposes, and with a
convenient separation: not too close for a good sensitivity to delay variations,
and not too far away in order to easily solve for the ambiguity in phase difference.
The pair H and K bands seems to be a good compromise, or more precisely
the ![]() band for reduced thermal contribution.
band for reduced thermal contribution.
With ![]() , and
, and ![]() , respectively
0.463 and 0.606
, respectively
0.463 and 0.606 ![]() m-1, the leading wavenumber will be:
m-1, the leading wavenumber will be:
![]()
| (21) |
Fringe patterns are shown in Fig. 2, for four different values of
the delay length L,
ranging from 0 to
30 m. The amplitude or pattern envelope is here solely determined by
the coherence due to the width and shape of the bandpath filters in each observed
bands, and the source emission spectrum is supposed to be flat.
With a square-shaped bandpath filter of width ![]() , centered at
, centered at ![]() , and with resolution
, and with resolution ![]() , the coherence is
, the coherence is
![]() with i=H or
with i=H or ![]() , l being the additional delay relative to zero group
delay, in each band. The relative bandwidth at the two observed wavebands is supposed
to be 0.1, or R = 10. The effect of longitudinal dispersion is clearly seen on the
position of maximum coherence, shifted on either side of zero delay.
, l being the additional delay relative to zero group
delay, in each band. The relative bandwidth at the two observed wavebands is supposed
to be 0.1, or R = 10. The effect of longitudinal dispersion is clearly seen on the
position of maximum coherence, shifted on either side of zero delay.
Another choice could be the J and ![]() bands. With
bands. With ![]() , and
, and ![]() , respectively 0.463 and
0.80
, respectively 0.463 and
0.80 ![]() m-1, the leading wavenumber being:
m-1, the leading wavenumber being:
![]() m-1, or
m-1, or ![]() m,
that is within the H band.
With
m,
that is within the H band.
With ![]() , a
, a ![]() variation in phase difference is obtained
for
variation in phase difference is obtained
for ![]() m, and a sensitivity of about 1 phase degree per 8 nm.
The phase ambiguity is here more critical, but this could be solved with a third
band observation, for example in the H band.
m, and a sensitivity of about 1 phase degree per 8 nm.
The phase ambiguity is here more critical, but this could be solved with a third
band observation, for example in the H band.
A third choice would be the two guiding wavenumbers in the same near-IR band, say the
![]() band. The difference between the two wavenumbers cannot exceed about
0.05
band. The difference between the two wavenumbers cannot exceed about
0.05 ![]() m-1, so that a
m-1, so that a ![]() variation is reached for
variation is reached for ![]() m, and the sensitivity is about 1 phase degree per 62 nm. This last choice can
be thought of as a preliminary or complementary setup for finding the fringe pattern,
the
m, and the sensitivity is about 1 phase degree per 62 nm. This last choice can
be thought of as a preliminary or complementary setup for finding the fringe pattern,
the ![]() pair being favored for high precision measurements.
pair being favored for high precision measurements.
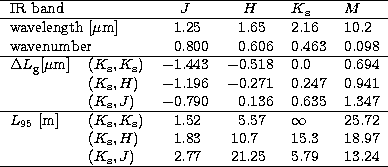 |
The residual group delay (18) is a linear function of the delay length. It is given in
Table 1,
for the J, H, ![]() and M bands, per meter of delay length at Paranal.
It has to be kept much smaller than the coherence length for fringes to be observed,
and the effect will be more stringent at shorter wavelength. The coherence is given by
and M bands, per meter of delay length at Paranal.
It has to be kept much smaller than the coherence length for fringes to be observed,
and the effect will be more stringent at shorter wavelength. The coherence is given by
![]() where l now stands for the residual group delay
where l now stands for the residual group delay ![]() . The air delay length L95 responsible for a 5% visibility
loss, with relative bandwidth of 0.1, has been estimated in the 4 bands, and is given
in Table 1. The three just mentioned choices for the guiding wavenumbers have
been
considered.
. The air delay length L95 responsible for a 5% visibility
loss, with relative bandwidth of 0.1, has been estimated in the 4 bands, and is given
in Table 1. The three just mentioned choices for the guiding wavenumbers have
been
considered.
Glass compensation plates will be needed with delay lengths larger than about 20
meters and the ![]() pair for fringe tracking (Fig. 2). The problem has been investigated by
Lévêque (1997)
for the VLTI delay lines, and the same kind of results is obtained with our
approximation for the air dispersive component. Let
pair for fringe tracking (Fig. 2). The problem has been investigated by
Lévêque (1997)
for the VLTI delay lines, and the same kind of results is obtained with our
approximation for the air dispersive component. Let ![]() the glass refractive
index, N'0 and N''0 respectively its first and second derivatives wrt
wavenumber at
the glass refractive
index, N'0 and N''0 respectively its first and second derivatives wrt
wavenumber at ![]() . The addition of a glass plate with thickness e in
one of the interferometer arms gives a group delay change
. The addition of a glass plate with thickness e in
one of the interferometer arms gives a group delay change ![]() :
:
![\begin{displaymath}
E(\sigma) \simeq
\left[
N(\sigma) - 1 + \sigma\frac{\partial N}{\partial \sigma}
\right]
\cdot e\end{displaymath}](/articles/aas/full/1999/14/ds1718/img85.gif) |
(22) |
| (23) |
 |
(24) |
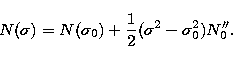 |
(25) |
The thickness of the glass plate will be ![]() .
.
The glass plate will add an additional delay at ![]() , given by (22) with
, given by (22) with
![]() , so that the air delay line has to be moved accordingly. This
jump has not to be known exactly if we accept a different interferometer offset
, so that the air delay line has to be moved accordingly. This
jump has not to be known exactly if we accept a different interferometer offset
![]() for each added compensation plate, the offset being determined
through astrometric calibration of the instrument, with the observation of reference
stars.
for each added compensation plate, the offset being determined
through astrometric calibration of the instrument, with the observation of reference
stars.
With the proposed scheme for fringe tracking and air-filled delay lines, phase
measurements are performed in two wavebands at non zero residual group delay. The
measured phase ![]() is then dependent on the shape of the observed spectrum, and
given by:
is then dependent on the shape of the observed spectrum, and
given by:
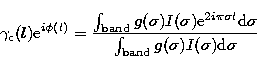 |
(26) |
The phase measured in the two guiding bands can be written:
| (27) |
The residual group delay has to be much smaller than the coherence length
![]() for a large enough coherence module, so that fine structures in the
source emission spectrum will have negligeable effects on the residual phase. As we
are concerned with astrometric measurements and large bandwidth observations, the
observed spectrum is supposed to be characterized by a single parameter, the color
temperature
for a large enough coherence module, so that fine structures in the
source emission spectrum will have negligeable effects on the residual phase. As we
are concerned with astrometric measurements and large bandwidth observations, the
observed spectrum is supposed to be characterized by a single parameter, the color
temperature ![]() of the equivalent black body radiation spectrum:
of the equivalent black body radiation spectrum:
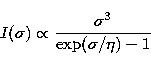 |
(28) |
The "spectrum phase'' is shown in Fig. 3 in terms of the air delay
length for the ![]() and H bands, and for different values of the color temperature parameter, ranging
from 2 300 K to 10 000 K. The pic of the black body emission spectrum is found at
2.16
and H bands, and for different values of the color temperature parameter, ranging
from 2 300 K to 10 000 K. The pic of the black body emission spectrum is found at
2.16 ![]() m for
m for ![]() K, so that the "spectrum phase'' is
nearly zero in the
K, so that the "spectrum phase'' is
nearly zero in the ![]() band for the first curve. In the H band, a similar
situation occurs for
band for the first curve. In the H band, a similar
situation occurs for ![]() 3 095 K, that is in between curves labelled
number 2 and 3. The coherence module does not show any significant dependence on the
temperature of the black body spectrum.
3 095 K, that is in between curves labelled
number 2 and 3. The coherence module does not show any significant dependence on the
temperature of the black body spectrum.
For air delay much larger than L95, Fig. 3 shows that the spectrum
phase deviation is not linear with the delay length, particularly in the H band. The
consequence is a dependence of the relative delay offset ![]() with the delay
length:
with the delay
length:
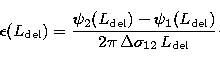 |
(29) |
![\begin{figure}
\includegraphics [width=8cm,clip]{ds1718f4.eps}\end{figure}](/articles/aas/full/1999/14/ds1718/Timg110.gif) |
Figure 4: Relative delay offset due to the non uniformity of the observed spectrum, characterized by its color temperature. Zero delay offset is for a flat spectrum, and the three curves are for the different pairs of guiding wavenumbers (Table 1) |
Relative to flat emission spectra with guiding wavenumbers ![]() and
and
![]() , the mean observed wavenumbers are now
, the mean observed wavenumbers are now ![]() and
and ![]() , and the true leading wavenumber
, and the true leading wavenumber ![]() is now dependent on
the source color temperature. Let
is now dependent on
the source color temperature. Let ![]() . With the derivative of the residual group delay wrt leading
wavenumber, the chromatic delay departure is:
. With the derivative of the residual group delay wrt leading
wavenumber, the chromatic delay departure is:
| (30) |
Copyright The European Southern Observatory (ESO)