Phase measurements have to be performed in two wavebands for fringe tracking with air-filled delay lines, and the useful quantity or "observable'' is their difference. In each band, phase is continuously changing with the air delay, typically 2 rad per meter, so that the measured phase is not constrained. Two schemes can be considered, for beam combination in a pupil plane:
1) Optical path modulation has been implemented on the first interferometer
prototype for optical astrometry (Shao & Staelin 1980), and later on
the MkIII interferometer (Shao et al. 1988), with one wavelength stroke
and 4-quadrants measurements. The problem of fringe ambiguity was partly solved with
the two-color method which, in the visible, greatly reduced the atmospheric piston
effect (Colavita et al. 1987). A more sophisticated technique, with
channeled spectrum and delay modulation is implemented on NPOI (Armstrong et al.
1998). This technique gives the fringe amplitude and phase as function of
wavenumber. Due to the larger wavelength range of the instrument, about an octave,
the stroke is twice the mean wavelength, with 8 samples per scan length. Both with
MkIII and NPOI, a single output of the beam combiner is used for fringe measurement.
Another approach is to have a 2-quadrants optical path modulation (![]() )with simultaneous measurements of the two complementary outputs of the beam
combination (Tango & Twiss 1980).
)with simultaneous measurements of the two complementary outputs of the beam
combination (Tango & Twiss 1980).
![\begin{figure}
\includegraphics [width=8cm,clip]{ds1718f5.eps}\end{figure}](/articles/aas/full/1999/14/ds1718/Timg119.gif) |
Figure 5: Basic principle of the two-beam combination in pupil plane, with 4 output phases and wide bands |
2) Simultaneous in-phase and quadrature-phase measurements can be obtained with
two combinations as shown in Fig. 5, and a ![]() phase shift in
one of the interferometer arm for the quadrature-phase combination. Phase
measurements being performed in two different wavebands, the phase shift has to be
achromatic which is possible with a polarization splitter and two total reflections in
glass material, e.g. an achromatic Fresnel rhomb retarder.
phase shift in
one of the interferometer arm for the quadrature-phase combination. Phase
measurements being performed in two different wavebands, the phase shift has to be
achromatic which is possible with a polarization splitter and two total reflections in
glass material, e.g. an achromatic Fresnel rhomb retarder.
We compare the sensitivity for phase measurements in a single band, either with path
length modulation and 4-quadrants measurements (scheme 1), or with quadrature-phase
combination (scheme 2). Let I0 the incoming source flux, in each interferometer
arm, and T0 the 4-steps scan duration in scheme 1 or the integration time in
scheme 2. Neglecting instrumental losses, the number
of useful photons per measurement and per arm is n0=I0T0. With equal
intensity splitting before beam combinations, the 4 outputs of
Fig. 5 are, in each band:
![\begin{displaymath}
J_{k} = \frac{n_{0}}{2} [1+\gamma\cos(\phi + \theta_{k})]\end{displaymath}](/articles/aas/full/1999/14/ds1718/img121.gif) |
(31) |
with ![]() .
.
The useful quantities for phase measurements are:
 |
(32) |
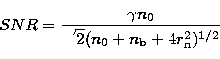 |
(33) |
In this sensitivity estimate, we have considered only photon noise and readout noise.
In a real situation, visibility fluctuations due to phase corrugations of the
wavefront (e.g. Lawson et al. 1999) should be considered as
additional atmospheric noise in SNR estimates with optical path modulation. On the
other hand, only scintillation noise has to be added in the average SNR estimate of
the quadrature-phase scheme, n0 being replaced by ![]() in the
denominator of (32) where
in the
denominator of (32) where ![]() is the scintillation index, as seen by the
detector.
is the scintillation index, as seen by the
detector.
The value of the leading wavenumber is not measured directly, it is deduced from the
effective guiding pair (![]() ). The relative uncertainty
on group delay, and hence on astrometric precision is, with the
). The relative uncertainty
on group delay, and hence on astrometric precision is, with the ![]() pair
and conditions prevailing at Paranal:
pair
and conditions prevailing at Paranal: ![]() where
where ![]() is the relative uncertainty on the
leading wavenumber. That is to say the simple model used here for the air refractive
index will be adequate for reaching single-field astrometric precision of a few
milliarcseconds, or a few parts in 108. For dual-field operations, the
uncertainty requirement on differential delay is much more stringent, about one part
in 1010, that is
is the relative uncertainty on the
leading wavenumber. That is to say the simple model used here for the air refractive
index will be adequate for reaching single-field astrometric precision of a few
milliarcseconds, or a few parts in 108. For dual-field operations, the
uncertainty requirement on differential delay is much more stringent, about one part
in 1010, that is ![]() . It means that the light beams
from the two observed stars have to cross as much as possible the same dispersive
media, band filters, and more generally optical parts. This is why we are
investigating a time multiplex scheme for dual-field astrometry, phase measurements in
one or the other field being performed without optical path modulation.
. It means that the light beams
from the two observed stars have to cross as much as possible the same dispersive
media, band filters, and more generally optical parts. This is why we are
investigating a time multiplex scheme for dual-field astrometry, phase measurements in
one or the other field being performed without optical path modulation.
With added glass compensation plates, the situation may not be so simple for
astrometric calibration of the instrument. Relation (25) for the glass refractive
index might not be realized exactly, a consequence being uncontrolled variations of the
leading wavenumber ![]() with delay length.
with delay length.
For group delay tracking, the "observable'' quantity is a difference
in residual phase between two wavebands ![]() and
and ![]() , and the residual
group delay is vanishing for the leading wavenumber
, and the residual
group delay is vanishing for the leading wavenumber ![]() . In the approximation
made for the air refractive index, keeping only the
. In the approximation
made for the air refractive index, keeping only the ![]() term in its
development, the
term in its
development, the ![]() value is not dependent on the ambient parameters, and
the approximation is valid to a few parts in 103, neglecting the water vapor
contribution.
value is not dependent on the ambient parameters, and
the approximation is valid to a few parts in 103, neglecting the water vapor
contribution.
On the other hand, the residual phase in the two wavebands ![]() and
and
![]() is, with (17) and (20):
is, with (17) and (20):
| (34) |
The sensitivity to path length variations of ![]() is larger than the
sensitivity of group delay measurement, the gain factor being
is larger than the
sensitivity of group delay measurement, the gain factor being ![]() , that is about 7.5 for the (
, that is about 7.5 for the (![]() pair. Once coherencing is achieved, optical path delay tracking with phase locking in
one or the other waveband could be used, in a more sensitive way than group delay
tracking alone. But a model for the residual phase variations with air delay length is
needed, so that the interest of phase locking has to be demonstrated with a real
experiment.
pair. Once coherencing is achieved, optical path delay tracking with phase locking in
one or the other waveband could be used, in a more sensitive way than group delay
tracking alone. But a model for the residual phase variations with air delay length is
needed, so that the interest of phase locking has to be demonstrated with a real
experiment.
Group delay tracking will operate only with a significant SNR in each wavebands, say
larger than 5. The uncertainty in the phase difference will then be smaller than
![]() rad, or about 16 degrees per individual measurement. With about 50
measurements per second, a 1 degree rms value, or 20 nm with the
(
rad, or about 16 degrees per individual measurement. With about 50
measurements per second, a 1 degree rms value, or 20 nm with the
(![]() pair, is reached after 5 seconds of observing time.
Such a sensitivity to path length
variations is considered to be good enough for conveniently averaging the atmospheric
piston in single-field astrometry, the duration of each observing sequence being
larger than a few 10 seconds. For dual-field astrometry with two bright sources, the
sensitivity in differential atmospheric piston will be
pair, is reached after 5 seconds of observing time.
Such a sensitivity to path length
variations is considered to be good enough for conveniently averaging the atmospheric
piston in single-field astrometry, the duration of each observing sequence being
larger than a few 10 seconds. For dual-field astrometry with two bright sources, the
sensitivity in differential atmospheric piston will be ![]() times the previous
figure, that is better than 10 nm in a 45 s observing sequence, or better than 0.1
mas/sequence with a 30-40 m baseline, which is also considered as a consistent
sensitivity figure.
times the previous
figure, that is better than 10 nm in a 45 s observing sequence, or better than 0.1
mas/sequence with a 30-40 m baseline, which is also considered as a consistent
sensitivity figure.
Copyright The European Southern Observatory (ESO)