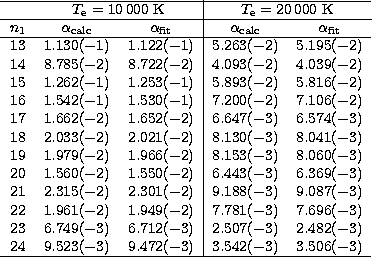
In Table 5 we give recombination coefficients for the 5g (![]() )levels at temperatures of
)levels at temperatures of ![]() K and
K and ![]() K, and a density of
103 cm-3, calculated from Eq. (1) and from the fitting
formulae given in Sect. 3.1. These are provided as a benchmark for the use
of the formulae. The comparison shows that the fitted coefficients
K, and a density of
103 cm-3, calculated from Eq. (1) and from the fitting
formulae given in Sect. 3.1. These are provided as a benchmark for the use
of the formulae. The comparison shows that the fitted coefficients
![]() agree with the calculated ones
agree with the calculated ones ![]() within
within ![]() .The
intensities of any of the lines in the 5g - 4f transition array may be
obtained, within the range of validity of the fits
(
.The
intensities of any of the lines in the 5g - 4f transition array may be
obtained, within the range of validity of the fits
(![]() K and
K and
![]() ),
by combining the
recombination coefficients calculated from the formulae of Sect. 3.1 with
the branching ratios in Table 2.
),
by combining the
recombination coefficients calculated from the formulae of Sect. 3.1 with
the branching ratios in Table 2.
 |
![\begin{figure}
\includegraphics [width=8cm]{ds8521f1.eps}
\includegraphics [wid...
...width=8cm]{ds8521f4.eps}
\includegraphics [width=8cm]{ds8521f5.eps}\end{figure}](/articles/aas/full/1999/10/ds8521/Timg84.gif) |
Figure 1:
Synthetic recombination spectra for the 5g - 4f transition array
at electron temperature |
In Fig. 1 we show synthetic spectra of the entire 5g - 4f transition
array calculated at ![]() K and various electron
densities. The lines are taken to have a FWHM of
K and various electron
densities. The lines are taken to have a FWHM of ![]() Å. Some of the lines show a pronounced variation in
intensity with density at typical nebular densities, between 102 and
104 cm-3. The line at 4434.6 Å, for example, which is the only
transition from the (2P
Å. Some of the lines show a pronounced variation in
intensity with density at typical nebular densities, between 102 and
104 cm-3. The line at 4434.6 Å, for example, which is the only
transition from the (2P![]() )5g 3H6 level (level 21
in Table 1) increases in intensity by a factor of 5.3 between
)5g 3H6 level (level 21
in Table 1) increases in intensity by a factor of 5.3 between
![]() and 104 cm-3 as the population of the
O3+ 2P
and 104 cm-3 as the population of the
O3+ 2P![]() rises. The intensity of this line, which is
one of the stronger lines in the 5g - 4f group, is
1.99 N(O3+)/N(H+) relative to H
rises. The intensity of this line, which is
one of the stronger lines in the 5g - 4f group, is
1.99 N(O3+)/N(H+) relative to H![]() at
at ![]() K and
K and ![]() cm-3, where N(O3+) and
N(H+) are the number densities of
O3+ and H+ respectively.
cm-3, where N(O3+) and
N(H+) are the number densities of
O3+ and H+ respectively.
The coefficients ![]() given in Table 4 show that the direct
photorecombination and cascade contributions to each level are dominated by
contributions from one or other of the O3+ parent states,
2P
given in Table 4 show that the direct
photorecombination and cascade contributions to each level are dominated by
contributions from one or other of the O3+ parent states,
2P![]() , indicating that the 5g levels are approaching
jj-coupling. We have investigated the effects of the interaction of the
two series on the line intensities by carrying out a calculation of the
coefficients in which there is no interaction. In this simpler
approximation, we use hydrogenic recombination coefficients throughout.
The recombination coefficients to the 5g
, indicating that the 5g levels are approaching
jj-coupling. We have investigated the effects of the interaction of the
two series on the line intensities by carrying out a calculation of the
coefficients in which there is no interaction. In this simpler
approximation, we use hydrogenic recombination coefficients throughout.
The recombination coefficients to the 5g ![]() levels are directly
proportional to the series parent population as follows:
levels are directly
proportional to the series parent population as follows:
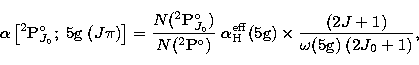 |
(10) |
To demonstrate the difference between the two approximations, we compare
synthetic spectra for the two models in Fig. 2 at the lowest
electron density, ![]() cm-3. At this density
the fraction of the O3+ population in the
2P
cm-3. At this density
the fraction of the O3+ population in the
2P![]() is very low (2%), so that in the approximation
of Eq. (10), the Rydberg states (2P
is very low (2%), so that in the approximation
of Eq. (10), the Rydberg states (2P![]() )nl
have very low populations and the resulting lines are weak, while in the
more realistic approximation of Eq. (1), population can be
transferred between the (2P
)nl
have very low populations and the resulting lines are weak, while in the
more realistic approximation of Eq. (1), population can be
transferred between the (2P![]() )nl and
(2P
)nl and
(2P![]() )nl series increasing the line intensities. It
should be noted that the differences between the two approximations become
smaller as the density increases and the parent state populations approach
the Boltzmann distribution.
)nl series increasing the line intensities. It
should be noted that the differences between the two approximations become
smaller as the density increases and the parent state populations approach
the Boltzmann distribution.
![\begin{figure}
\includegraphics [width=11cm]{ds8521f6.eps}\end{figure}](/articles/aas/full/1999/10/ds8521/Timg91.gif) |
Figure 2:
Synthetic recombination spectra for the 5g - 4f transition array
at electron temperature |
Copyright The European Southern Observatory (ESO)