We base our calculation of the recombination coefficients on a model of the
O2+ ion including the two series
1s22s22p(2P![]() nl and
1s22s22p(2P
nl and
1s22s22p(2P![]() )nl. At low electron densities
)nl. At low electron densities
![]() , the population of the ground levels
, the population of the ground levels ![]() and
and ![]() in the recombining
ion O3+ differs significantly from the Boltzmann distribution.
The critical density, defined as the electron density at which the rate of
collisional de-excitation of 2P
in the recombining
ion O3+ differs significantly from the Boltzmann distribution.
The critical density, defined as the electron density at which the rate of
collisional de-excitation of 2P![]() is equal to the rate
of radiative de-excitation, is 7330 cm-3 at a temperature of 104 K.
Thus for typical nebular densities the relative populations of the levels of
the two series (2P
is equal to the rate
of radiative de-excitation, is 7330 cm-3 at a temperature of 104 K.
Thus for typical nebular densities the relative populations of the levels of
the two series (2P![]() nl and
(2P
nl and
(2P![]() )nl will depend on density (as well as
temperature
)nl will depend on density (as well as
temperature ![]() ).
).
To calculate recombination coefficients ![]() and effective recombination coefficients for the lines originating from the
5g (
and effective recombination coefficients for the lines originating from the
5g (![]() ) levels, we consider the contribution to
the 5g level population made both by direct recombination from the two
parent levels and by cascades within the same series and between the
two series. For sufficiently high orbital angular momentum of the valence
electron, jj-coupling prevails and the population of a given level depends
only on the population of other levels with the same parent and on direct
recombination from that parent state. The 4f and 5g levels lie at
intermediate orbital angular momentum where neither LS- nor jj-coupling
are good descriptions.
We calculate the recombination coefficients
to the 5g (
) levels, we consider the contribution to
the 5g level population made both by direct recombination from the two
parent levels and by cascades within the same series and between the
two series. For sufficiently high orbital angular momentum of the valence
electron, jj-coupling prevails and the population of a given level depends
only on the population of other levels with the same parent and on direct
recombination from that parent state. The 4f and 5g levels lie at
intermediate orbital angular momentum where neither LS- nor jj-coupling
are good descriptions.
We calculate the recombination coefficients
to the 5g (![]() ) levels from the expression
) levels from the expression
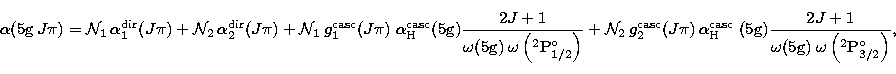 |
(1) |
In Eq. (1), the ![]() (i=1,2) are the direct radiative recombination coefficients to the
(i=1,2) are the direct radiative recombination coefficients to the
![]() level. These coefficients were computed from the
appropriate photoionization cross-sections obtained from the R-matrix
calculations performed in the Breit-Pauli approximation described in
Sect. 2.
level. These coefficients were computed from the
appropriate photoionization cross-sections obtained from the R-matrix
calculations performed in the Breit-Pauli approximation described in
Sect. 2.
The third and fourth terms in Eq. (1) are the cascade
contributions. The coefficients
![]() are the combined cascade
contributions to all 5g levels calculated in a hydrogenic approximation.
These coefficients were obtained using the methods described by Storey &
Hummer (1995) and include full allowance for all radiative and
collisional processes between excited states, and as a result depend upon
both temperature and density.
We assume that the fraction of the cascading
represented by the coefficient
are the combined cascade
contributions to all 5g levels calculated in a hydrogenic approximation.
These coefficients were obtained using the methods described by Storey &
Hummer (1995) and include full allowance for all radiative and
collisional processes between excited states, and as a result depend upon
both temperature and density.
We assume that the fraction of the cascading
represented by the coefficient
![]() that falls on a particular
level 5g (
that falls on a particular
level 5g (![]() ) is proportional to its statistical weight and also that
there are cascade contributions from states of both parentage. The fraction
from each parent is given by the coefficients g
) is proportional to its statistical weight and also that
there are cascade contributions from states of both parentage. The fraction
from each parent is given by the coefficients g![]() and
g
and
g![]() , which are determined from the photoionization
cross-sections from the state 5g (
, which are determined from the photoionization
cross-sections from the state 5g (![]() ) at the two parent thresholds.
) at the two parent thresholds.
The coefficients
![]() in Eq. (1) can be computed as follows.
We have fitted the coefficients
in Eq. (1) can be computed as follows.
We have fitted the coefficients
![]() as a function of temperature by:
as a function of temperature by:
| |
(2) |
The cascade contributions, ![]() , can
be fitted with a maximum error of
, can
be fitted with a maximum error of ![]() by a product of a function of
density and a function of temperature as follows:
by a product of a function of
density and a function of temperature as follows:
| |
(3) |
The fractional populations ![]() and
and ![]() can be
expressed as follows:
can be
expressed as follows:
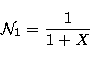 |
(4) |
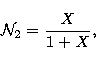 |
(5) |
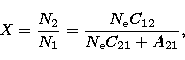 |
(6) |
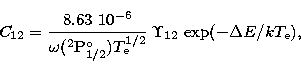 |
(7) |
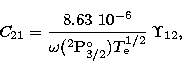 |
(8) |
The collision strengths ![]() were taken from the R-matrix
calculations of Blum & Pradhan (1992).
These can be fitted to
were taken from the R-matrix
calculations of Blum & Pradhan (1992).
These can be fitted to
| |
(9) |
 |
Finally, the fractions ![]() and
and
![]() can be obtained from Table 4.
can be obtained from Table 4.
In order to calculate recombination coefficients for any 5g level
of O2+ at a specific electron temperature ![]() and electron density
and electron density ![]() , one uses the expressions
for the coefficients from Eqs. (1), (2)
and (3), the data from Tables 3 and 4
and the recombining ion level population determined
from Eqs. (4-9).
, one uses the expressions
for the coefficients from Eqs. (1), (2)
and (3), the data from Tables 3 and 4
and the recombining ion level population determined
from Eqs. (4-9).
Copyright The European Southern Observatory (ESO)