2 Atomic data for O²⁺

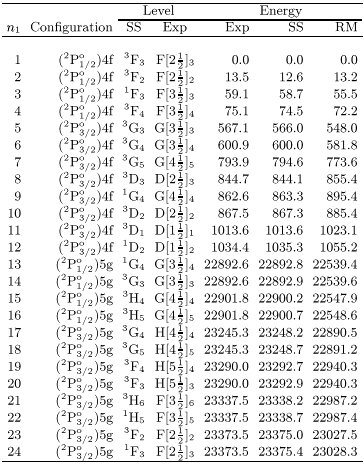
In Table 1 we present experimental and calculated level energies for the two electron configurations 1s²2s²2p4f and 1s²2s²2p5g. The experimental values are from Pettersson (1982), with the energies being given relative to the lowest levels of the 4f configuration in each case. Two different methods were used to obtain the theoretical results.

  

Table 1: Indices (n₁) and energy levels (in cm^-1) of the 4f and 5g states in O²⁺ ions. Experimental energy data are from Pettersson (1982) while theoretical values are from SUPERSTRUCTURE (SS) and an R-matrix (RM) calculation. We also give our theoretical (SS) and previous experimental (Moore 1970) level assignments

In the first approach, we used the general purpose atomic structure package SUPERSTRUCTURE (SS, Eissner et al. 1974; Nussbaumer & Storey 1978) to calculate wavefunctions for O²⁺. Only the 1s²2s²2p4f and 1s²2s²2p5g electron configurations were included in the calculation. The scaled Thomas-Fermi-Dirac potentials for the common radial basis functions were varied to minimize the sum of the energies of all twelve terms. The non-relativistic Hamiltonian matrix was adjusted empirically to give the best possible agreement between calculated term energies (obtained from the weighted mean of the fine-structure energies) and the experimental values. The 4f and 5g spin-orbit parameters were also adjusted empirically to give the best agreement between the calculated and experimental fine-structure level energies within the terms. This procedure was first implemented in SS by Zeippen et al. (1977). These empirical adjustments, although very small compared to the absolute energies of the levels, are important in obtaining accurate eigenvectors for levels of the same total angular momentum and parity ($J\pi$). It can be seen from Table 1 that the energy separations between such levels may be only a few tens of cm^-1. An error of a few wavenumbers in these energy separations can therefore cause significant errors in the eigenvectors, and since we cannot achieve this level of accuracy in our ab initio calculation, we make empirical corrections. The maximum difference in the energies between the empirically corrected SS calculation and experiment is 3.4 cm^-1, with an average of 1.2 cm^-1. In addition to the level assignments obtained from the SS calculation, we also provide level assignements from Moore (1970).

In our second theoretical approach, we use the R-matrix method (Berrington et al. 1987) in which bound-bound and bound-free radiative data for O²⁺ states are calculated from the O³⁺ + e^- scattering problem. Some relativistic terms are included in the Hamiltonian in the Breit-Pauli approximation. One-body energy shifts (the mass correction and the Darwin term) and the spin-orbit interaction are incorporated within this implementation of the R-matrix method (Scott & Taylor 1982; Berrington et al. 1995).

The O³⁺ target system is represented by the two ground levels 2p ²P$_{1/2}^\mathrm{o}$ and ²P$_{3/2}^\mathrm{o}$, with the wave function basis consisting of the 2s²2p and 2p³ configurations and with the target radial waves being obtained from SS. The experimental fine-structure splitting was used for the two target levels before constructing the Hamiltonian for the (N+1)-electron system, to compensate for the absence of two-body fine-structure terms in the Hamiltonian. The target fine-structure energy calculated including only the spin-orbit terms is 379.1 cm^-1 compared to the experimental value of 385.9 cm^-1. This empirical correction to the target energies is the only correction that can be made in the R-matrix approach. In particular no empirical corrections to the eigenvectors of the O²⁺ bound states can be made as was done in the SS calculation. As a result the accuracy of the calculated energies is significantly worse than in the SS calculation, with average differences of 13.1 cm^-1 for the 4f levels and 2.7 cm^-1 for the 5g levels (taken relative to the energetically lowest 5g level).

  

Table 2: Wavelengths in air $\lambda_\mathrm{air}$ (in Å), electric dipole transition probabilities A_n1,n2 (in s^-1) and branching ratios b_n1,n2 for the 5g - 4f transitions in O²⁺ ions. The indices n₁ and n₂ correspond to the energy level indices in Table 1

There is also a systematic shift of approximately 350 cm^-1 between the levels of the 5g and 4f configurations compared to experiment.

In view of the significantly higher accuracy of the empirically corrected SS level energies, we used this method to calculate the radiative transition data. Transition matrix elements were computed and combined with experimental energy level data to obtain the final transition probabilities which are given in Table 2. Also given in this table are wavelengths $\lambda_\mathrm{air}$ and branching ratios from each upper state. It should be noted that the wavelengths presented in Table 2 are derived from the experimental energy level data (Pettersson 1982) and may differ slightly from the observed wavelengths. These data will be used later to produce synthetic emission spectra of the 5g - 4f recombination lines.