

Up: Atomic data from the
Resonances appear as spikes or dips on the graph of 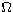 .
The spikes are sometimes isolated but more often they come as a dense forest
of peaks. Resonances can have a big effect on
.
The spikes are sometimes isolated but more often they come as a dense forest
of peaks. Resonances can have a big effect on  , especially
when the transition is optically forbidden, and may cause
, especially
when the transition is optically forbidden, and may cause
 to be between a few per cent or several factors larger than
the predictions of distorted wave approximations. For the purpose of
comparison we list in Table 5 results for
to be between a few per cent or several factors larger than
the predictions of distorted wave approximations. For the purpose of
comparison we list in Table 5 results for 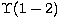 based on
collision strengths from (a) the IRON Project, (b) the IRON Project (chopped)
and (c) a distorted wave approximation. The collision strength in (b) was
obtained by imposing an arbitrary maximum peak height of
based on
collision strengths from (a) the IRON Project, (b) the IRON Project (chopped)
and (c) a distorted wave approximation. The collision strength in (b) was
obtained by imposing an arbitrary maximum peak height of 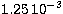 which effectively chops the tops off the resonance peaks. The distorted wave
collision strength used in (c) is from Bhatia & Mason (1986).
which effectively chops the tops off the resonance peaks. The distorted wave
collision strength used in (c) is from Bhatia & Mason (1986).
Table 5:
Showing the effect on 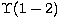 of chopping off
the IRON Project resonances: (a), IRON; (b) IRON (chopped); (c)
Bhatia
& Mason (1986)
of chopping off
the IRON Project resonances: (a), IRON; (b) IRON (chopped); (c)
Bhatia
& Mason (1986)
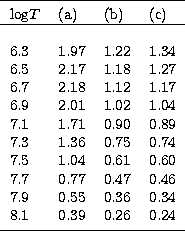 |
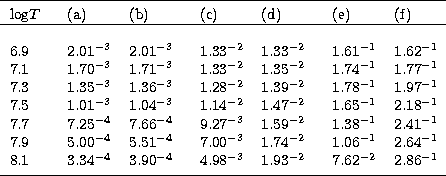
Table 6:
Showing how the high energy contribution to  increases
with temperature for three types of transition.
Intersytem (non electric dipole) transition:
(a)
increases
with temperature for three types of transition.
Intersytem (non electric dipole) transition:
(a) 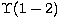 with
with 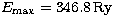 ;
(b)
;
(b) 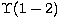 with
with 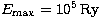 .
Intersystem (electric dipole) transition:
(c)
.
Intersystem (electric dipole) transition:
(c) 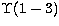 with
with 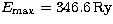 ;
(d)
;
(d) 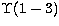 with
with 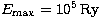 .
Electric dipole transition:
(e)
.
Electric dipole transition:
(e) 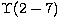 with
with 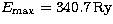 ;
(f)
;
(f) 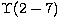 with
with 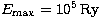 .
.
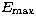 is the value used for the upper limit in the integral that
defines
is the value used for the upper limit in the integral that
defines  and it should in theory be
and it should in theory be 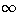 .
.
 |
As mentioned above, we use the Breit-Pauli R-matrix code for collision
energies up to 103.05816 Ry after which we replace it by the simpler LS
coupling code together with the algebraic code JAJOM (Saraph 1978). In this
way we are able to extend the Breit-Pauli results to higher energies by
running the LS code at 116, 127.5, 170, 250, 350 Ry. This sparse mesh is
ample for our purposes since no resonances are encountered over this energy
range. It is difficult to go much beyond 350 Ry using the R-matrix codes.
In order to obtain meaningful and reliable thermally averaged collision
strengths at the high temperatures given in Table 9 it is necessary to
know  at energies of one or two thousand rydbergs, i.e. well
beyond 350 Ry. We are able to make reasonable extrapolations of our data
by means of the computer program OmeUps (Burgess & Tully 1992).
at energies of one or two thousand rydbergs, i.e. well
beyond 350 Ry. We are able to make reasonable extrapolations of our data
by means of the computer program OmeUps (Burgess & Tully 1992).


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)



![]() at energies of one or two thousand rydbergs, i.e. well
beyond 350 Ry. We are able to make reasonable extrapolations of our data
by means of the computer program OmeUps (Burgess & Tully 1992).
at energies of one or two thousand rydbergs, i.e. well
beyond 350 Ry. We are able to make reasonable extrapolations of our data
by means of the computer program OmeUps (Burgess & Tully 1992).