

Up: Atomic data from the
Subsections
Paper I in this series gives the basic atomic theory, approximations and
computer codes used in the IRON Project. For electrons incident with kinetic
energies relative to the ground state of the target less than or equal to
350 Ry we make use of the R-matrix method based on the close coupling
approximation. This allows us to take account of channel
coupling up to the n=4 levels. Relativistic effects are allowed for,
either by using the Breit-Pauli version of the R-matrix code, or by
running the non-relativistic version and then carrying out an
algebraic transformation of the appropriate collision matrix elements by means
of Saraph's (1978) code JAJOM. We use the former procedure for energies below
116 Ry and the latter for energies from 116 to 350 Ry. We are able to
extend our R-matrix collision strengths beyond 350 Ry with some confidence
by using A. Burgess's graphics program OmeUps with the
appropriate high energy limits (see Burgess & Tully 1992). For the optically
allowed transitions the limits are determined by the oscillator strengths
(see Table 7), while for the non-exchange optically forbidden transitions we
have calculated the Born limits using the program discussed by
Burgess et al. (1997) and results are given in Table 8.
The radial orbitals for the Be-like target are as follows:
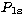 ,
, 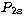 are from Clementi & Roetti (1974).
are from Clementi & Roetti (1974).
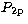 is the 2 exponent function
is the 2 exponent function
| 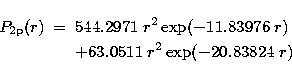 |
|
| (4) |
which we obtained by using Hibbert's (1975) variational program
CIV3 to minimise the sum of the energies of the
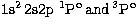 terms with trial exponents
and coefficients taken from the Opacity Project.
For the remaining orbitals Pnl, with
terms with trial exponents
and coefficients taken from the Opacity Project.
For the remaining orbitals Pnl, with
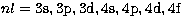 ,
we used the minimum number of exponents dictated by nl and calculated
their values, as given in Table 2, by minimising the sum of the energies
of the
,
we used the minimum number of exponents dictated by nl and calculated
their values, as given in Table 2, by minimising the sum of the energies
of the 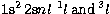 terms. We used the
minimization routine VA04A by setting IDAVID = 0 and IVA04A = 1.
(Note that the same procedure was adopted by
Berrington et al. (1998) in spite of the unintentionally contradictory statements
they make.) Furthermore, by setting MAXIT1 = 5 we limited the maximum
number of iterations to 5. Additional work by one of us (JAT) has shown that
some improvement can be obtained by using values of MAXIT1 larger than 5.
terms. We used the
minimization routine VA04A by setting IDAVID = 0 and IVA04A = 1.
(Note that the same procedure was adopted by
Berrington et al. (1998) in spite of the unintentionally contradictory statements
they make.) Furthermore, by setting MAXIT1 = 5 we limited the maximum
number of iterations to 5. Additional work by one of us (JAT) has shown that
some improvement can be obtained by using values of MAXIT1 larger than 5.
Our collision calculation makes use of theoretical target energies
produced by the Breit-Pauli R-matrix code. They are given in Table 3
along with the observed energies for some of the levels taken from
Corliss & Sugar (1982). Most of these observed values, with
some small differences, can also be found on the Web page of the National
Institute of Standards and Technology, http://physics.nist.gov.
As can be seen there is very good agreement between theory and experiment,
where we assume 1 Ry = 109737.32 cm-1. Finally, we find that the data
in Table 3 are in excellent agreement with results we have obtained
using Hibbert's (1975) atomic structure code CIV3.
In order to delineate the multitude of resonance peaks we ran the Breit-Pauli
code at 7704 values of the collision energy starting at 3.15210 Ry, relative
to the ground state, and going up to 103.05816 Ry.
Originally we meant to go as far as 115 Ry but finally abandoned this goal
because of the excessive amount of computer time required. We therefore
covered the interval between 103.05816 and 116 Ry by making a linear
extrapolation backwards using the values of the collision strength at 116 and
127.5 Ry. In a few cases, especially for optically allowed transitions, a
noticeable step up occurs in the collision strength when the energy increases
beyond 103.05816 Ry, see Fig. 2.
Table 2:
Exponents for the 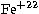 radial orbitals using
analytic forms similar to that shown in (4). The coefficients
are fixed by orthonormality conditions
radial orbitals using
analytic forms similar to that shown in (4). The coefficients
are fixed by orthonormality conditions
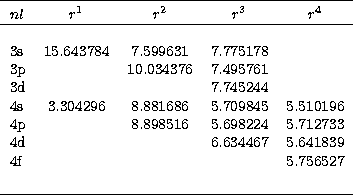 |
Table 3:
Fe XXIII level energies in rydberg units relative to the
ground state. Theoretical results from the Breit-Pauli R-matrix
program. Observed results from Corliss & Sugar (1982) assuming
1 Ry = 109737.32  . % diff is the
percentage difference between the theoretical and observed energies
. % diff is the
percentage difference between the theoretical and observed energies
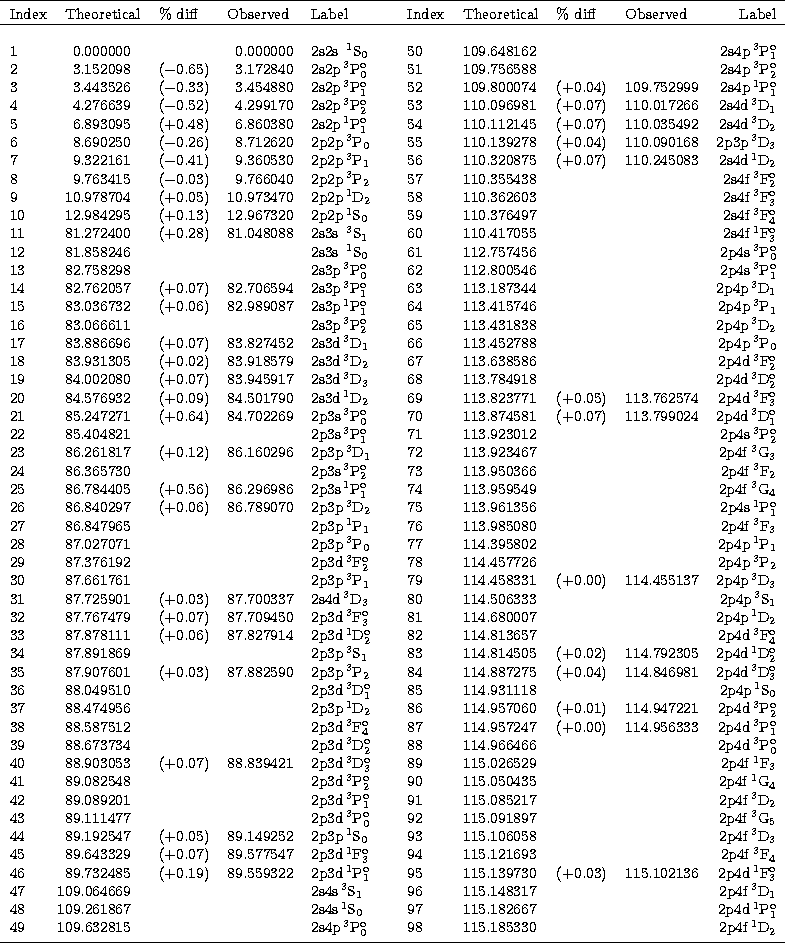 |
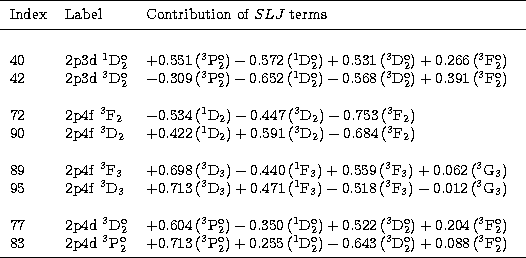
Table 4:
Labels chosen to identify levels dominated by the same SLJ term
 |
The 98 energy levels given in Table 3, together with the way of
indexing them, are from the Breit-Pauli branch of the R-matrix program.
Using the CIV3 code we have been able to make the identifications given in
the columns with the heading "Label'' . We use the customary procedure of
letting the label be the configuration with the largest absolute mixing
coefficient. However in four cases we abandoned this procedure in order
to avoid the confusing situation of having the same label for more than
one level. The last column in Table 4 shows
SLJ terms which make a significant contribution to each of 4 pairs of
levels where this problem arises. The mixing coefficients given in Table 4
are from CIV3 with ICSTAS = 1.
. We use the customary procedure of
letting the label be the configuration with the largest absolute mixing
coefficient. However in four cases we abandoned this procedure in order
to avoid the confusing situation of having the same label for more than
one level. The last column in Table 4 shows
SLJ terms which make a significant contribution to each of 4 pairs of
levels where this problem arises. The mixing coefficients given in Table 4
are from CIV3 with ICSTAS = 1.


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)
![]() ,
, ![]() are from Clementi & Roetti (1974).
are from Clementi & Roetti (1974).
![]() is the 2 exponent function
is the 2 exponent function
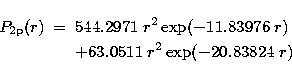
![]() terms with trial exponents
and coefficients taken from the Opacity Project.
For the remaining orbitals Pnl, with
terms with trial exponents
and coefficients taken from the Opacity Project.
For the remaining orbitals Pnl, with
![]() ,
we used the minimum number of exponents dictated by nl and calculated
their values, as given in Table 2, by minimising the sum of the energies
of the
,
we used the minimum number of exponents dictated by nl and calculated
their values, as given in Table 2, by minimising the sum of the energies
of the ![]() terms. We used the
minimization routine VA04A by setting IDAVID = 0 and IVA04A = 1.
(Note that the same procedure was adopted by
Berrington et al. (1998) in spite of the unintentionally contradictory statements
they make.) Furthermore, by setting MAXIT1 = 5 we limited the maximum
number of iterations to 5. Additional work by one of us (JAT) has shown that
some improvement can be obtained by using values of MAXIT1 larger than 5.
terms. We used the
minimization routine VA04A by setting IDAVID = 0 and IVA04A = 1.
(Note that the same procedure was adopted by
Berrington et al. (1998) in spite of the unintentionally contradictory statements
they make.) Furthermore, by setting MAXIT1 = 5 we limited the maximum
number of iterations to 5. Additional work by one of us (JAT) has shown that
some improvement can be obtained by using values of MAXIT1 larger than 5.

