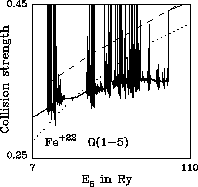$\begin{figure} \psfig {figure=0105-b.ps}\end{figure}$

Figure 2: Optically allowed: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

$\begin{figure} \psfig {figure=0103-a.ps}\end{figure}$

Figure 3: An optically allowed intersystem transition

**Table 7:** Line and oscillator strengths, S_ij and f_ij, from CIV3; results obtained using the length gauge. $\,(1.310^{-3} \equiv \, 1.310 \ 10^{-3})$
$\begin{tabular} {lllllllll} \noalign{\smallskip} \hline \noalign{\smallskip} $i$... ...80$^{-2}$\space \\ \noalign{\smallskip} \hline \noalign{\smallskip}\end{tabular}$

**Table 8:** High energy Born limits. $\,(4.778^{-5} \equiv \, 4.778 \ 10^{-5})$
$\begin{tabular} {ll} \noalign{\smallskip} \hline \noalign{\smallskip} $i-j$&${\s... ...77$^{-2}$\space \\ \noalign{\smallskip} \hline \noalign{\smallskip}\end{tabular}$

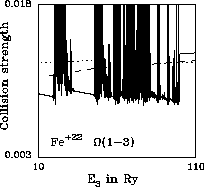$\begin{figure} \psfig {figure=0103-b.ps}\end{figure}$

Figure 4: Optically allowed intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

$\begin{figure} \psfig {figure=0109-a.ps}\end{figure}$

Figure 5: An optically forbidden (electric quadrupole) transition

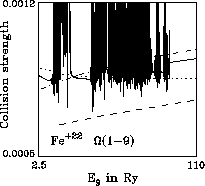$\begin{figure} \psfig {figure=0109-b.ps}\end{figure}$

Figure 6: Optically forbidden (electric quadrupole): full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992); dot-dashed, Chen & Ong (1998)

$\begin{figure} \psfig {figure=0102-a.ps}\end{figure}$

Figure 7: An optically forbidden intersystem transition

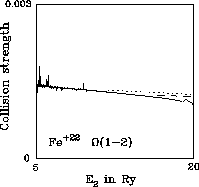$\begin{figure} \psfig {figure=0102-b.ps}\end{figure}$

Figure 8: Optically forbidden intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

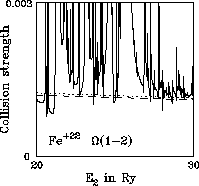$\begin{figure} \psfig {figure=0102-c.ps}\end{figure}$

Figure 9: Optically forbidden intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

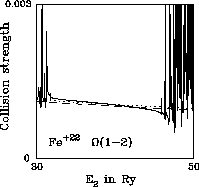$\begin{figure} \psfig {figure=0102-d.ps}\end{figure}$

Figure 10: Optically forbidden intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

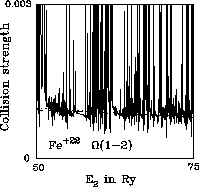$\begin{figure} \psfig {figure=0102-e.ps}\end{figure}$

Figure 11: Optically forbidden intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

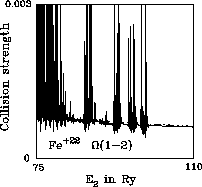$\begin{figure} \psfig {figure=0102-f.ps}\end{figure}$

Figure 12: Optically forbidden intersystem: full, present; dotted, Bhatia & Mason (1986); dashed, Zhang & Sampson (1992)

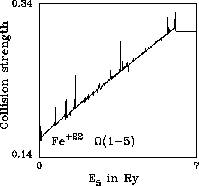
Figures 1 and 2 show ${\sl \Omega}(1 - 5)$ . This is an optically allowed transition meaning that the collision strength increases logarithmically with energy as $E_j \to \infty$ . In order to delineate the low energy resonances in Fig. 1 we use a magnified energy scale there compared to the one in Fig. 2.

Figures 3 and 4 show ${\sl \Omega}(1 - 3)$ . This is an intersystem transition that behaves as though it were optically allowed owing to the breakdown of LS coupling. For this to happen the initial and final levels must have different parities and $\Delta J = 0, \pm 1$ , subject to the condition that $J = 0 \not\to J' = 0$ .

Figures 5 and 6 show ${\sl \Omega}(1 - 9)$ . This is a forbidden transition in which neither the parity nor the spin change. The collision strength for this type of transition tends to a finite limiting value as $E_j \to \infty$ . We have used the methods discussed by Burgess et al. (1997) to calculate the Born limits for all such transitions between levels whose index does not exceed 10 (see Table 8).

Figures 7 to 12 show ${\sl \Omega}(1 - 2)$ . This is a forbidden intersystem transition for which the collision strength normally falls off like E_j^-2 in the high energy limit.

It is well known that when a new threshold is crossed the collision strength for a transition involving two lower levels will in general decrease, or sometimes increase, so that the collision strength in question behaves like a step function. This is explained by the influence of newly opened channels which cause a redistribution of the total electron flux to occur. The other thing to notice is the change in slope that occurs at the passage from the "low'' to the ``intermediate'' energy region. This may be the result of having calculated fewer partial waves in the "low'' energy region where we maintained $J \leq 5$ . We did however carry out a top-up procedure in order to account for the higher partial waves.

**Table 9:** $\rm Fe^{+22}$ effective collision strengths ${\sl \Upsilon}(i - j)$ for $6.3 \le \log T \le 8.1$ . $\,(2.421^{-3} = \, 2.421 \ 10^{-3})$

4 Family portraits