In the previous two sections we discussed a technique to make the random error approach its lower bound quite closely but, whatever procedure one follows, one will need to assess the actual random error on a radial velocity measurement. In order to do so one can always apply straightforward error progression which naturally takes into account the effect of all operations actually performed on the data. The result for a simple case is given in the Appendix (Eq. (A9)), but one immediately perceives that its evaluation is rather tedious. This may be the reason why alternatives have been sought such as error progression with strong approximations (Murdoch & Hearnshaw 1991), the lower bound (Sect. 2) itself, or the so-called r-statistic.
Tonry & Davis (1979)
computed the well known error estimate
![]() on a cross-correlation derived radial velocity shift,
using only properties of the cross-correlation function itself:
on a cross-correlation derived radial velocity shift,
using only properties of the cross-correlation function itself:
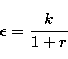 |
(9) |
 |
(10) |
![\begin{displaymath}
{\sigma_{\rm a}}^{2} = \frac{1}{2N} \sum_{n} [ c(\delta + n) - c(\delta - n) ] ^{2}\end{displaymath}](/articles/aas/full/1999/09/h1238/img58.gif) |
(11) |
Peterson (1983)
reported differences, which correlated with the line width
of the spectrum, between this theoretical error estimate
and the true errors.
Experimenting with simple synthetic spectra and (portions of) early-type
spectra,
Verschueren (1991)
found that estimating B in practice was to a
large extent arbitrary.
He found empirically that ![]() , with w the FWHM of the
cross-correlation peak, gives excellent agreement with Monte-Carlo simulated
random errors.
Kurtz et al. (1992)
then showed analytically that, for sinusoidal
noise with a half-width equal to the half-width of the correlation peak,
k must equal 3w/8, which is now widely in use.
, with w the FWHM of the
cross-correlation peak, gives excellent agreement with Monte-Carlo simulated
random errors.
Kurtz et al. (1992)
then showed analytically that, for sinusoidal
noise with a half-width equal to the half-width of the correlation peak,
k must equal 3w/8, which is now widely in use.
The r-parameter was intended to describe systematic object-template mismatch as well as random noise (Tonry, private communication, 1998) and was developed and successfully tested on late-type spectra (see Kurtz & Mink 1998 for an update and overview). In this section, we investigate the applicability of the so-called r-statistic to purely random errors (i.e. in the absence of systematic mismatch) for early-type spectra.
Caution when applying the r-statistic to other than
late-type spectra is justified since, in a strict sense, the relation
(9) does not exist. For the simple case described in the Appendix,
the explicit expressions (A9), (A12)
show that the expected squared error ![]() and the expected
and the expected
![]() depend on the structure of the
spectrum in a different way:
both take the form of a weighted average of the flux variances on individual
pixels, but the weights (A10), (A13) may be quite different;
moreover,
depend on the structure of the
spectrum in a different way:
both take the form of a weighted average of the flux variances on individual
pixels, but the weights (A10), (A13) may be quite different;
moreover, ![]() depends on the fit-interval while
depends on the fit-interval while
![]() does not.
So, in general one cannot expect to find a
relation between the two which is independent of the nature of the spectrum.
While Monte-Carlo simulations with a given
spectrum and different noise levels
will reveal a strict correlation between the observed error
and
does not.
So, in general one cannot expect to find a
relation between the two which is independent of the nature of the spectrum.
While Monte-Carlo simulations with a given
spectrum and different noise levels
will reveal a strict correlation between the observed error
and ![]() , the actual
relation between those quantities must depend on the structure of the spectrum.
In other words, there cannot be a "generally valid" expression for k.
The fact that the error estimate (9) does appear to work
for all late-type
spectra must be due to the fact that the latter, viewed over a sufficiently
large wavelength region and with a pixel-size not much smaller
than the typical
width of a spectral feature, all do have the appearance of a strongly
fluctuating function: as a consequence, the weights
(A10) and (A13) become approximately independent of n.
In fact, this appearance of late-type stars corresponds qualitatively to the
main condition imposed by
Tonry & Davis (1979),
that the Fourier power spectrum of the "perfect
correlation function" (i.e. the signal function, c0(i) in our notation)
should be very similar to the
one of the "remainder function" (i.e. the noise function c(i) - c0(i)).
Since the expression (9) has the benefit of being simple,
elegant and intuitively appealing,
we have investigated in detail whether it might also in some way be applied to
early-type spectra.
, the actual
relation between those quantities must depend on the structure of the spectrum.
In other words, there cannot be a "generally valid" expression for k.
The fact that the error estimate (9) does appear to work
for all late-type
spectra must be due to the fact that the latter, viewed over a sufficiently
large wavelength region and with a pixel-size not much smaller
than the typical
width of a spectral feature, all do have the appearance of a strongly
fluctuating function: as a consequence, the weights
(A10) and (A13) become approximately independent of n.
In fact, this appearance of late-type stars corresponds qualitatively to the
main condition imposed by
Tonry & Davis (1979),
that the Fourier power spectrum of the "perfect
correlation function" (i.e. the signal function, c0(i) in our notation)
should be very similar to the
one of the "remainder function" (i.e. the noise function c(i) - c0(i)).
Since the expression (9) has the benefit of being simple,
elegant and intuitively appealing,
we have investigated in detail whether it might also in some way be applied to
early-type spectra.
 |
For early-type spectra, which generally contain broader lines, and/or when
cross-correlating selected small spectral regions (as often required for such
spectra, see e.g. the arguments in
Verschueren 1995;
Verschueren et al. 1999b),
the cross-correlation function consists of much
broader features than is the case for late-type stars.
In order to illustrate this point in a very
simple way, we performed a Monte-Carlo experiment using a
spectrum consisting of one Gaussian absorption line surrounded by
different amounts of continuum. Table 1 shows that
only when the cross-correlation function predominantly consists
of relatively narrow features (large N),
the correct error is obtained from ![]() ;
for small N, the cross-correlation function is dominated by the
relatively broad central peak, resulting in a too low value for
the error owing to a decreased
;
for small N, the cross-correlation function is dominated by the
relatively broad central peak, resulting in a too low value for
the error owing to a decreased ![]() .
.
Similar experiments were then performed on different spectral regions
of synthetic early-type spectra, comparing the error estimate
![]() with the true random error from the Monte-Carlo dispersion
for different amounts of added random noise.
Figure 8 shows results for
4 different spectra.
These results are only indicative for the differences between
with the true random error from the Monte-Carlo dispersion
for different amounts of added random noise.
Figure 8 shows results for
4 different spectra.
These results are only indicative for the differences between ![]() and the true error that may occur, and should not be used in a
quantitative sense.
In general, Gaussian line shapes or rotation profiles yield too
small error estimates
and the true error that may occur, and should not be used in a
quantitative sense.
In general, Gaussian line shapes or rotation profiles yield too
small error estimates ![]() ,
while lorentzian line shapes produce too large
values probably due to their relatively large FWHM w.
We conclude that, except for late-type spectra, the predicted
error
,
while lorentzian line shapes produce too large
values probably due to their relatively large FWHM w.
We conclude that, except for late-type spectra, the predicted
error ![]() may be very incorrect, and that moreover a generalisation
to early-type spectra would be impossible because the required
proportionality constant k would depend on the details of each
individually selected spectrum (e.g. line shape, amount of continuum pixels
included as shown in Table 1, mixture of metallic, He
and H lines, etc.).
may be very incorrect, and that moreover a generalisation
to early-type spectra would be impossible because the required
proportionality constant k would depend on the details of each
individually selected spectrum (e.g. line shape, amount of continuum pixels
included as shown in Table 1, mixture of metallic, He
and H lines, etc.).
Two other important problems related to the practical computation
of ![]() in the framework of early-type stars are worth mentioning.
First, the cross-correlation function is often composed of overlapping
broad components so that the FWHM w of the central
peak looses the significance assumed in the r-statistic.
Secondly, it is assumed
(Tonry & Davis 1979)
that
in the framework of early-type stars are worth mentioning.
First, the cross-correlation function is often composed of overlapping
broad components so that the FWHM w of the central
peak looses the significance assumed in the r-statistic.
Secondly, it is assumed
(Tonry & Davis 1979)
that ![]() is computed with respect to the exact central position of the
cross-correlation function. In practice, one evidently has to use
the measured central position, which yields the same result provided
that the width of the central peak is much smaller than the complete
cross-correlation function. In case small spectral regions are selected,
the computation of
is computed with respect to the exact central position of the
cross-correlation function. In practice, one evidently has to use
the measured central position, which yields the same result provided
that the width of the central peak is much smaller than the complete
cross-correlation function. In case small spectral regions are selected,
the computation of ![]() with respect to the measured
centre can be quite different from its correct value.
For example, the value of
with respect to the measured
centre can be quite different from its correct value.
For example, the value of ![]() in Table 1 for N=32 and N=64 would (further) decrease
to 0.009 and 0.045, respectively, if computed with respect to the measured
centre of the cross-correlation peak.
in Table 1 for N=32 and N=64 would (further) decrease
to 0.009 and 0.045, respectively, if computed with respect to the measured
centre of the cross-correlation peak.
Copyright The European Southern Observatory (ESO)