

Up: Random-error minimization during cross-correlation
Random errors set a theoretical upper limit to the radial velocity precision
attainable from a given spectrum. Quantifications of this
minimum error as a function of the intrinsic morphology of the spectrum and
of its random errors were computed by several authors
(Connes 1985;
Merline 1985;
Brown 1989;
Butler et al. 1996).
These results all assume that the observed spectrum is compared with a
noise-free reference spectrum.
The latter is of course not the case when cross-correlating with
observed templates.
In addition, many different templates
are required to closely match the different spectral types
when dealing with early-type spectra, which
makes it more difficult to acquire all of them with a very high S/N.
We therefore derived a generalised
expression for the minimum random error on a cross-correlation shift in the
presence of random errors on both object and template.
In order to be able to consider sub-pixel errors, we assume throughout that
the spectra are oversampled which is a condition generally met for
early-type spectra at intermediate and high resolution (see also Sect. 3).
Assume an object spectrum 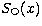 and an intrinsically identical
template spectrum
and an intrinsically identical
template spectrum  which have been sampled (i.e. integrated)
in N pixels
with constant pixel-size
which have been sampled (i.e. integrated)
in N pixels
with constant pixel-size  (the x-coordinate may in general be
any function of wavelength
(the x-coordinate may in general be
any function of wavelength  ). We assume both spectra to be
multiplicatively normalised to an identical but
otherwise arbitrary flux level.
We use the
dimensionless coordinate p defined
by the transformation
). We assume both spectra to be
multiplicatively normalised to an identical but
otherwise arbitrary flux level.
We use the
dimensionless coordinate p defined
by the transformation  so
that its integer values
so
that its integer values  correspond to the central positions of the
pixels and we conveniently refer to it as the "pixel number".
Let I(p) denote the sampled, normalised and noise-free spectrum,
and
correspond to the central positions of the
pixels and we conveniently refer to it as the "pixel number".
Let I(p) denote the sampled, normalised and noise-free spectrum,
and  and
and  the random noise on object and
template spectrum, respectively, at that same flux level.
Following the argument of
Brown (1989),
we can calculate the apparent shift
the random noise on object and
template spectrum, respectively, at that same flux level.
Following the argument of
Brown (1989),
we can calculate the apparent shift 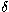 , due to noise only,
between these two spectra by minimizing
, due to noise only,
between these two spectra by minimizing
| ![\begin{displaymath}
f(\delta) = \sum_{p} W(p) [I(p) + N_{\rm O}(p)
- I(p + \delta) - N_{\rm T} (p)]^{2}.\end{displaymath}](/articles/aas/full/1999/09/h1238/img11.gif) |
(1) |
Note that maximizing the cross-correlation function is indeed equivalent
to a least-squares minimization of the difference between the two spectra (see e.g.
Furenlid & Furenlid 1990).
The statistical weight W(p)
must equal the inverse of the variance on the difference spectrum:
|  |
(2) |
where  denotes the expectation value.
Approximating
denotes the expectation value.
Approximating  for well sampled spectra and sufficiently small
for well sampled spectra and sufficiently small 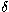 ,
where the derivative is indeed the
derivative of the sampling values with respect to the coordinate p,
we obtain
,
where the derivative is indeed the
derivative of the sampling values with respect to the coordinate p,
we obtain
| ![\begin{displaymath}
\delta = \frac{\sum_{p} W(p) [N_{\rm O}(p)
- N_{\rm T}(p)]\...
...um_{p} W(p)
\left(
\frac{{\rm d}I}{{\rm d}p}
\right)^{2}}\cdot\end{displaymath}](/articles/aas/full/1999/09/h1238/img15.gif) |
(3) |
Denoting the variance on 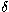 by
by 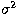 =
=  ,one finds
,one finds
|  |
|
| |
| (4) |
For the sake of clarity, we repeat that
 and
and  are the variances on both spectra after normalisation,
and that
are the variances on both spectra after normalisation,
and that  is expressed in units of pixel number p.
If the spectra are binned into pixels of constant
pixel-size in x = log(
is expressed in units of pixel number p.
If the spectra are binned into pixels of constant
pixel-size in x = log( ), which is required for computing a
Doppler shift, one must multiply
), which is required for computing a
Doppler shift, one must multiply  by the
pixel-size in log(
by the
pixel-size in log( ) units times c to obtain a velocity.
The standard deviation
) units times c to obtain a velocity.
The standard deviation  represents a lower bound for the expected
random error on the measured shift of one sampled and noisy
spectrum with respect to an intrinsically identical one.
In fact the derivation assumes that the underlying (noiseless)
structure of the spectra is known with infinite resolution and that this
information can be used to find the shift.
Even though (4) will therefore not always
provide a realistic error estimate, it is very important as a reference value.
represents a lower bound for the expected
random error on the measured shift of one sampled and noisy
spectrum with respect to an intrinsically identical one.
In fact the derivation assumes that the underlying (noiseless)
structure of the spectra is known with infinite resolution and that this
information can be used to find the shift.
Even though (4) will therefore not always
provide a realistic error estimate, it is very important as a reference value.
A similar result has been obtained long before in signal-processing
theory: if one replaces the statistical weight in
(2) by a constant one describing additive,
wavelength-independent noise,
then the expression for the expected error on the time-delay of a radar signal
is recovered exactly. This is particularly interesting since
Woodward & Davies (1950)
derived this result without making a first-order approximation like the one
leading to (3) so that this approximation probably does not restrict
the validity of (4) to spectra with high S/N.
However,
Woodward (1953)
does point
out that there is a S/N-level above which it certainly
cannot be meaningful anymore, i.e. the so-called ambiguity limit which was
estimated by
Fellgett (1953) to be about 3 for astronomical spectra.
One can trivially rewrite the variances on object and template
appearing in Eq. (4) in terms of their S/N:
| ![\begin{displaymath}
\langle N_{\rm O}^{2}(p)\rangle + \langle N_{\rm T}^{2}(p)\r...
...{\rm O}^{2}(p)} +
\frac{1}{(S/N)_{\rm T}^{2}(p)}
\right]\cdot\end{displaymath}](/articles/aas/full/1999/09/h1238/img22.gif) |
(5) |
In the common case of spectra I(p) being normalised to their
continuum level, one may straightforwardly express the variances
on these spectra as a function of their original continuum level
( ) and of their original read-out
noise (
) and of their original read-out
noise ( ), both expressed in photon units:
), both expressed in photon units:
|  |
(6) |
Note that the continuum level and
read-out noise in this expression refer to those of
the one-dimensional spectrum, thus after a possible extraction.
In the case of pure photon noise, identical S/N of object and template
spectrum, a series of L
separated identical Gaussian absorption lines of width  ,
central depth d (
,
central depth d ( ), and signal-to-noise in the continuum
), and signal-to-noise in the continuum
 , Eq. (4) can be
written as
, Eq. (4) can be
written as
|  |
(7) |
where the only approximation made is replacing the sum by an integral.
f(d) is a weak monotonous function of d, being 0.94 for 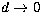 and 2.01 for d=1.
and 2.01 for d=1.  and
and  are expressed in
pixels. The factor
are expressed in
pixels. The factor  is absent in case of a noise-free template.
is absent in case of a noise-free template.
For Gaussian emission lines with a peak signal-to-noise in their centre
equal to  , a negligible continuum intensity, and otherwise
similar parameters as above, one finds
, a negligible continuum intensity, and otherwise
similar parameters as above, one finds
|  |
(8) |
where the last numerical factor is about 0.63.
Both the latter expressions may be useful for quick estimates of the intrinsic
radial velocity precision of a (portion of a) spectrum, and give
insight in the dependence of that precision on the spectrum parameters.


Up: Random-error minimization during cross-correlation
Copyright The European Southern Observatory (ESO)
![]() and an intrinsically identical
template spectrum
and an intrinsically identical
template spectrum ![]() which have been sampled (i.e. integrated)
in N pixels
with constant pixel-size
which have been sampled (i.e. integrated)
in N pixels
with constant pixel-size ![]() (the x-coordinate may in general be
any function of wavelength
(the x-coordinate may in general be
any function of wavelength ![]() ). We assume both spectra to be
multiplicatively normalised to an identical but
otherwise arbitrary flux level.
We use the
dimensionless coordinate p defined
by the transformation
). We assume both spectra to be
multiplicatively normalised to an identical but
otherwise arbitrary flux level.
We use the
dimensionless coordinate p defined
by the transformation ![]() so
that its integer values
so
that its integer values ![]() correspond to the central positions of the
pixels and we conveniently refer to it as the "pixel number".
Let I(p) denote the sampled, normalised and noise-free spectrum,
and
correspond to the central positions of the
pixels and we conveniently refer to it as the "pixel number".
Let I(p) denote the sampled, normalised and noise-free spectrum,
and ![]() and
and ![]() the random noise on object and
template spectrum, respectively, at that same flux level.
Following the argument of
Brown (1989),
we can calculate the apparent shift
the random noise on object and
template spectrum, respectively, at that same flux level.
Following the argument of
Brown (1989),
we can calculate the apparent shift ![]() , due to noise only,
between these two spectra by minimizing
, due to noise only,
between these two spectra by minimizing
![\begin{displaymath}
f(\delta) = \sum_{p} W(p) [I(p) + N_{\rm O}(p)
- I(p + \delta) - N_{\rm T} (p)]^{2}.\end{displaymath}](/articles/aas/full/1999/09/h1238/img11.gif)

![\begin{displaymath}
\delta = \frac{\sum_{p} W(p) [N_{\rm O}(p)
- N_{\rm T}(p)]\...
...um_{p} W(p)
\left(
\frac{{\rm d}I}{{\rm d}p}
\right)^{2}}\cdot\end{displaymath}](/articles/aas/full/1999/09/h1238/img15.gif)

![\begin{displaymath}
\langle N_{\rm O}^{2}(p)\rangle + \langle N_{\rm T}^{2}(p)\r...
...{\rm O}^{2}(p)} +
\frac{1}{(S/N)_{\rm T}^{2}(p)}
\right]\cdot\end{displaymath}](/articles/aas/full/1999/09/h1238/img22.gif)

![]() ,
central depth d (
,
central depth d (![]() ), and signal-to-noise in the continuum
), and signal-to-noise in the continuum
![]() , Eq. (4) can be
written as
, Eq. (4) can be
written as

![]() , a negligible continuum intensity, and otherwise
similar parameters as above, one finds
, a negligible continuum intensity, and otherwise
similar parameters as above, one finds
