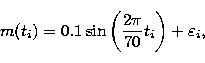
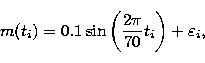
![\begin{figure}
\hspace*{5mm} \mbox{
\subfigure[]{
\psfig {file=ds8030f4a.eps,he...
...subfigure[]{
\psfig {file=ds8030f4b.eps,height=80mm,width=80mm}
}
}\end{figure}](/articles/aas/full/1999/08/ds8030/Timg51.gif) |
Figure 4: Simulated sinusoidal process with noise. a) regular time sampling, b) irregular time sampling for the star HIP 111771 |
![\begin{figure}
\hspace*{5mm} \mbox{
\subfigure[]{
\psfig {file=ds8030f5a.eps,he...
...subfigure[]{
\psfig {file=ds8030f5b.eps,height=80mm,width=80mm}
}
}\end{figure}](/articles/aas/full/1999/08/ds8030/Timg52.gif) |
Figure 5:
Estimated variograms (above |
In order to show conspicuously the differences between the two
estimators when the signal is perturbed by outliers, we took
the previous simulated data and changed only one value.
We put it at ![]() from the mean. Actually, this
value can sometimes occur in real data from Hipparcos. The effect
of the substitution of that single value can be seen in
Fig. 5b, which should be compared with the Fig. 5a.
Several remarks can be made. First, the
from the mean. Actually, this
value can sometimes occur in real data from Hipparcos. The effect
of the substitution of that single value can be seen in
Fig. 5b, which should be compared with the Fig. 5a.
Several remarks can be made. First, the ![]() estimator shows a flat and slight declining curve around the
period: the signature of the periodicity has totally
disappeared. In comparison, the general behaviour of
estimator shows a flat and slight declining curve around the
period: the signature of the periodicity has totally
disappeared. In comparison, the general behaviour of
![]() has not changed. Second, the estimation of
the micro-scale variability
has not changed. Second, the estimation of
the micro-scale variability ![]() jumped with
jumped with
![]() . Furthermore, there is a higher jump at the
second lag, which would suggest that there is some variability
in the signal for extremely short time-scales. Again
. Furthermore, there is a higher jump at the
second lag, which would suggest that there is some variability
in the signal for extremely short time-scales. Again
![]() stays unchanged. With this example we see that
stays unchanged. With this example we see that
![]() is not reliable when outlying values are
present in the data, and that
is not reliable when outlying values are
present in the data, and that ![]() is more invariant
to such values, i.e.
is more invariant
to such values, i.e. ![]() is a highly robust estimate
of the variogram.
is a highly robust estimate
of the variogram.
Copyright The European Southern Observatory (ESO)