3 Co-adding measurements

The planned scanning strategy of Planck goes stepwise: at each step the satellite will spin about 100 times around a fixed axis, covering the same circular scan, then the spin axis of the satellite will be moved by a few arc-minutes, and so on. This provides two types of redundancy: every pixel along each circle will be scanned about 100 times, and some pixels will be seen by several circles, with different orientations of the focal plane. In this section we show, assuming a perfect white noise along each scan, that the properties of the error matrix of the Stokes parameters coming from OC's are kept if all data are simply co-added at each pixel, whatever the orientations of the focal plane. The redundancy provided by intersecting circles can be used to remove the stripes induced on maps by low-frequency noise in the data streams. An extension adapted to polarised measurements of the method proposed by Delabrouille (1998) for the de-striping of Planck maps is studied in Revenu et al. (1999).

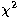Here we assume that the noise is not correlated between different scans and can thus be described by one matrix ${\bf N}_l$ for each scan, indexed by l, passing through the pixel. The $\chi^2$ is then the sum of the $\chi^2_l$over the L scans that cross the pixel:

$$\begin{eqnarray} \chi^2=\sum_{l=1}^L({\bf M}_l-{\bf A}_l\,{\bf S}) ^{ T}{{\bf N}_l}^{-1}({\bf M} _l-{\bf A}_l\, {\bf S}).\end{eqnarray}$$ (17)

The estimator of the Stokes parameters stemming from this 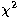$\chi^2$ is

$$\begin{eqnarray} {\bf S} = \left(\sum_{l=1}^L {\bf A}_l^{ T}\, {\bf N}_l^{-1}\,... ...t)^{-1}\,\sum_{l=1}^L{\bf A}_l^{ T}\, {\bf N}_l^{-1}\, {\bf M}_l, \end{eqnarray}$$ (18)

with variance matrix:

$$\begin{eqnarray} {\bf V} = \left(\sum_{l=1}^L {\bf A}_l^{ T}\, {\bf N}_l^{-1} \,{\bf A}_l\right)^{-1}.\end{eqnarray}$$ (19)

In the ideal case,

for a given scan, the noise (assumed to be white on each scan) has the same variance for all bolometers with no correlation between them, although it can vary from one scan to the other:

$$\begin{eqnarray} {\bf N}_l = {\sigma_{l}}^2 {\mathchoice {\rm 1\mskip-4mu l} {\rm 1\mskip-4mu l} {\rm 1\mskip-4.5mu l} {\rm 1\mskip-5mu l}}, \end{eqnarray}$$ (20)

and one can write the resulting variance combining the L scans:

$$\begin{eqnarray} {\bf V}_L = \left(\sum_{l=1}^L \frac{{\bf X}_l}{{\sigma_l}^2}\r... ... R}^{-1}(\psi_l)\,{\bf X}_1\, {\bf R}(\psi_l)\right)^{-1}\!\!\!\!,\end{eqnarray}$$ (21)

where ${\bf X}_l = {\bf A}_l^{T}\,{\bf A}_l$, and we have written explicitly the rotation matrices which connect the orientation of the focal plane along scan l with that along scan 1. Note that these matrices are dependent of the position along the scan through angle $\psi_l$.

If the observing setup is in an OC, all orientation dependence drops out and the expression of the covariance matrix becomes diagonal as for a single measurement (Eq. 9):

$$\begin{eqnarray} {\bf V}_{0\,L} = \frac{4\,{\sigma_L}^2}{n\,L} \left(\begin{arr... ... \\ \end{array}\right) = \frac{{\sigma_L}^2}{L}\,{{\bf X}_0}^{-1},\end{eqnarray}$$ (22)

where ${{\bf X}_0}^{-1}$ is defined in Eq. 9 and the average noise level $\sigma_L$ is defined as:

$$\begin{eqnarray} \frac{1}{{\sigma_L}^2} = \left\langle\frac{1}{{\sigma_l}^2}\right\rangle. \end{eqnarray}$$ (23)

Of course one recovers the fact that, with L measurements, the errors on the Stokes parameters are reduced by a factor $\sqrt{L}$.

More realistically,

we expect that the noise matrices will take a form similar to Eq. 12:

$$\begin{eqnarray} {\bf N}_l = {\sigma_l}^2 \left({\mathchoice {\rm 1\mskip-4mu l}... ...mu l} {\rm 1\mskip-5mu l}}+ \hat{\beta}_l + \hat{\gamma}_l\right).\end{eqnarray}$$ (24)

If $\hat{\beta}_l$ and $\hat{\gamma}_l$ are small, first order inversion allows to calculate $\bf{V}$ (${\bf V}_{ L}$ is given by Eq. 22):

$$\begin{eqnarray} {\bf V} = {\bf V}_{ L} +{\bf V}_{ L} \sum_{l=1}^L {\bf A}_l^{ ... ...at{\beta}_l + \hat{\gamma}_l}{{\sigma_l}^2} {\bf A}_l{\bf V}_{ L}.\end{eqnarray}$$ (25)

If the focal plane is in an OC, this expression simplifies to

$$\begin{eqnarray} {\bf V}_{ L} = \frac{{\sigma_{ L}}^2}{L}\, \left({{\bf X}_0}^{-... ...rac{\hat{\mathcal{B}}_l+\hat{\mathcal{G}}_l}{{\sigma_l}^2}\right),\end{eqnarray}$$ (26)

where

$$\begin{eqnarray} \left(\begin{array} {l} \hat{\mathcal{B}}_l\\ \hat{\mathcal{G}}... ...l\end{array}\right) \,{\bf A}_1\ {{\bf X}_0}^{-1} {\bf R}(\psi_l).\end{eqnarray}$$ (27)

The 1/L factor inside the parenthesis in equation (27) implies that the cross-correlations and the dependence on on the orientation $\psi_l$of the focal plan remain weak when one cumulates measurements of the same pixel.