4 The error covariance matrix of the scalar E and B parameters

Scalar polarisation parameters, denoted E and B, have been introduced, which do not depend on the reference frame (Newman & Penrose 1966; Zaldarriaga & Seljak 1997). However, the properties of OC's do not propagate simply to the error matrix of the E and B parameters because their definition is non local in terms of the Stokes parameters.

Nevertheless, if the measurements errors are not correlated between different points of the sky (or if the correlation has been efficiently suppressed by the data treatment) then the elements of the error matrix of the multipolar coefficients a_E,lm and a_B,lm can be written in a simple form which is given in Appendix B for a general configuration.

For an OC, the error matrix simplifies further and its elements reduce to:

$$\begin{eqnarray} & <\delta a_{^E_B, lm}\,{\delta a_{^E_B, l''m''}}^*\gt = \frac{... ...{\hat{\bf n}}_k)}^*\,{}_{-2}Y_{l''m''}({\hat{\bf n}}_k)]\nonumber.\end{eqnarray}$$

where N_pix is the total number of pixels in the sky, $\sigma^{}_{\mathrm{Stokes}}$ is the common r.m.s. error on the Q and U Stokes parameters, ${\hat{\bf n}}_k$ is the direction of pixel k and functions $_{\pm 2}Y_{lm}({\hat{\bf n}}_k)$ are the spin 2 spherical harmonics. If $\sigma^{}_{\mathrm{Stokes}}$ does not depend on the direction in the sky, a highly improbable situation, then the orthonormality of the spin weighted spherical harmonics makes the error matrix fully diagonal in the limit of a large number of pixels:

$$\begin{eqnarray} & \left( \begin{array} {cc} <\delta a_{E, lm}\,{\delta a_{E, l'... ...\sigma_{\mathrm{Stokes}}^2\ \delta_{ll''} \delta_{mm''}\nonumber. \end{eqnarray}$$

Note that, even for unpolarised data, the error matrix between multipolar amplitude is not diagonal unless the r.m.s. error is constant over the whole sky (see for instance Oh, Spergel & Hinshaw 1998).

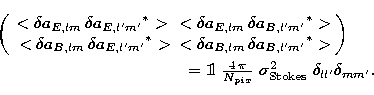In the same conditions, the noise matrix of fields E and B is also fully diagonal:

$$\left(\begin{array} {cc} \left<\delta E({\hat{\bf n}})\ \del... ...ma_{\mathrm{Stokes}}^2\ \delta_{{\hat{\bf n}}\,{\hat{\bf n}}'}.$$