

Up: Optimised polarimeter configurations for
Subsections
If we assume that the measurements 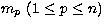 have identical
and decorrelated errors
have identical
and decorrelated errors
( ), the
), the 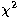 is simply:
is simply:
| ![\begin{displaymath}
\chi^2 = \frac{1}{\sigma^2} \sum_{p=1}^n\left[m_{ p}-
\frac{1}{2}(I + Q\,\cos 2\alpha_{ p} + U\,\sin 2\alpha_{p})\right]^2,\end{displaymath}](/articles/aas/full/1999/06/ds7941/img23.gif) |
(6) |
and the inverse of the covariance matrix of the Stokes parameters is given by:
It is shown in the appendix that, if the orientations of the
polarimeters are evenly distributed on 180 :
:
|  |
(7) |
the matrix  takes the very simple diagonal form:
takes the very simple diagonal form:
| 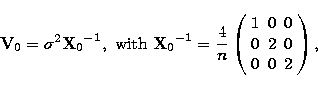 |
(8) |
independent of the orientation of the focal plane, while its determinant is
minimised.
In other words, at the same time, the errors on the Stokes parameters
get decorrelated, their error matrix becomes independent of the
orientation of the focal plane and the volume of the error ellipsoid takes its
smallest possible value:  .
.
The "Optimised Configurations'' (OC) are the sets of polarimeters
which satisfy condition
(8), (see Fig. 1).
![\begin{figure}
\includegraphics [width=8.8cm]{ds7941OCS.eps}\end{figure}](/articles/aas/full/1999/06/ds7941/Timg29.gif) |
Figure 1:
The relative orientations of polarimeters in "Optimised Configurations'' with 3, 4 and 5
detectors |
They are hereafter referred to by the
subscript as in Eq. 9.
The smallest OC involves three polarimeters with relative angle
 .
With 4 polarimeters, the angular separation must be
.
With 4 polarimeters, the angular separation must be  , and so
on. Note that
a configuration with one unpolarised detector
and 2 polarised detectors can never measure the Stokes parameters with
uncorrelated errors, because this would require polarimeters oriented
90
, and so
on. Note that
a configuration with one unpolarised detector
and 2 polarised detectors can never measure the Stokes parameters with
uncorrelated errors, because this would require polarimeters oriented
90 apart from each other, which would not allow the breaking of the
degeneracy between Q and U.
apart from each other, which would not allow the breaking of the
degeneracy between Q and U.
If one combines several OC's with several unpolarised
detectors, all uncorrelated with each other, the resulting covariance
matrix for the Stokes
parameters remains diagonal and independent of the orientation of
the various OC's. More precisely, when combining the measurements
of n T unpolarised detectors (temperature measurements), with n P
polarised detectors arranged in OC's,
the covariance matrix of the Stokes parameters reads:
| 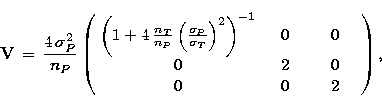 |
(9) |
where we have introduced inverse average noise levels,
 and
and  , for the unpolarised and polarised
detectors respectively:
, for the unpolarised and polarised
detectors respectively:
|  |
(10) |
Note that the levels of noise can be different from one OC
to the other and from those of the unpolarised detectors.
In general one expects that there will be some slight imbalance and
cross-correlation between the noise of the detectors.
The noise matrix of the measurements will in general take the form:
| 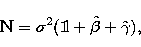 |
(11) |
where the imbalance  and cross-correlation
and cross-correlation 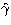 matrices
matrices
|  |
|
| (12) |
are "small'', that is will be treated as first order perturbations
in the following, and therefore

To this order, the variance matrix of the Stokes parameters is easily
obtained from Eq. (5):
| ![\begin{eqnarray}
{\bf V} = \sigma^2 \left[{\bf X}^{-1} + \hat{\mathcal{B}}+ \hat{\mathcal{G}}\right],\end{eqnarray}](/articles/aas/full/1999/06/ds7941/img41.gif) |
(13) |
where the matrix  is given by Eq. 7 and the first
order corrections to
is given by Eq. 7 and the first
order corrections to  , matrices
, matrices 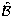 and
and  , read:
, read:
| 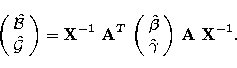 |
(14) |
In an OC, the matrix  takes the simple diagonal form
takes the simple diagonal form
 of
Eq. (9), and the non diagonal parts,
of
Eq. (9), and the non diagonal parts, 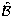 and
and  remain
of order 1 in
remain
of order 1 in  and
and 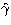 . For instance, if we consider an OC
with 3 polarimeters, and polarimeter number 1 is oriented in the x
direction,
. For instance, if we consider an OC
with 3 polarimeters, and polarimeter number 1 is oriented in the x
direction,

where  , and
, and
|  |
|
| (15) |
Note that 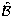 and
and  transform under a rotation of the focal
plane by a rotation
transform under a rotation of the focal
plane by a rotation  :
:
|  |
(16) |
Because 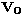 is invariant, as long as
is invariant, as long as  and
and 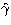 are
small the dependence of
are
small the dependence of  on the orientation of the focal plane
remains weak.
on the orientation of the focal plane
remains weak.


Up: Optimised polarimeter configurations for
Copyright The European Southern Observatory (ESO)
![\begin{displaymath}
\chi^2 = \frac{1}{\sigma^2} \sum_{p=1}^n\left[m_{ p}-
\frac{1}{2}(I + Q\,\cos 2\alpha_{ p} + U\,\sin 2\alpha_{p})\right]^2,\end{displaymath}](/articles/aas/full/1999/06/ds7941/img23.gif)
![\begin{displaymath}
\chi^2 = \frac{1}{\sigma^2} \sum_{p=1}^n\left[m_{ p}-
\frac{1}{2}(I + Q\,\cos 2\alpha_{ p} + U\,\sin 2\alpha_{p})\right]^2,\end{displaymath}](/articles/aas/full/1999/06/ds7941/img23.gif)


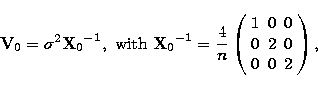
![\begin{figure}
\includegraphics [width=8.8cm]{ds7941OCS.eps}\end{figure}](/articles/aas/full/1999/06/ds7941/Timg29.gif)
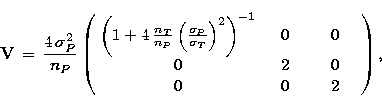



![\begin{eqnarray}
{\bf V} = \sigma^2 \left[{\bf X}^{-1} + \hat{\mathcal{B}}+ \hat{\mathcal{G}}\right],\end{eqnarray}](/articles/aas/full/1999/06/ds7941/img41.gif)


![]() and
and ![]() transform under a rotation of the focal
plane by a rotation
transform under a rotation of the focal
plane by a rotation ![]() :
:
