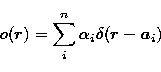
The goal of myopic deconvolution is to restore both the object and the PSF knowing the image intensity measurements and the a priori information.
We model our observed object (field of
stars) by a sum of Dirac functions (Gunsay & Jeffs 1995). Its intensity is then given by:
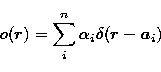 |
(2) |
A constant or slowly variable parameter can also be added to account for sky
background and underlying emission (Lucy 1994).
The deconvolution method we use is based on a stochastic approach i.e., we consider object parameters and PSF as outcomes of stochastic processes (Conan 1998).
Bayes' rule combines the likelihood of the data with the a priori
distribution of the parameters (object and PSF, which are decorraleted processes) into the
a posteriori
probability distribution of the unknowns (![]() and h):
and h):
| |
(3) |
![]() reflects the a priori knowledge (or prior) on the object
parameters. In addition to the reparametrization itself, which
contains a strong constraint on the object, we also use:
reflects the a priori knowledge (or prior) on the object
parameters. In addition to the reparametrization itself, which
contains a strong constraint on the object, we also use:
Similarly, p(h) reflects the a priori knowledge on the PSF. It can be
reasonably assumed to be Gaussian and is therefore characterized
by its first and second moments (Conan et al. 1998): a mean PSF (![]() ) and a Power Spectral Density
[PSD]
(
) and a Power Spectral Density
[PSD]
(![]() ). This PSD can be viewed as a per frequency variance of
the Optical Transfer Function [OTF] (Fourier Transform of the PSF) around its mean value.
). This PSD can be viewed as a per frequency variance of
the Optical Transfer Function [OTF] (Fourier Transform of the PSF) around its mean value.
The method used to calculate ![]() and
and ![]() using the Wave-front sensor (WFS) data or the
image of a
reference star will be described in Sect. 4.
using the Wave-front sensor (WFS) data or the
image of a
reference star will be described in Sect. 4.
Following the Maximum A Posteriori (MAP) approach, a set of estimated parameters is given
by the maximization of ![]() , the a posteriori probability law:
, the a posteriori probability law:
| |
(4) |
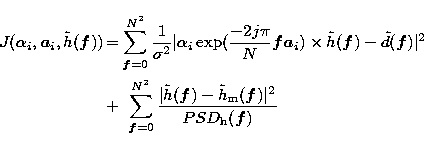 |
||
| (5) |
The first term of Eq. (5), is the likelihood term which takes into account the object reparametrisation.
The second term is a regularization term on the PSF. It
draws the actual OTF towards its mean value ![]() with a stiffness
related to its PSD. This term avoids a noise propagation and
amplification on the PSF (cf. Sect. 5) as well as the trivial solution (PSF = image and all the sources = 0
except one delta function).
with a stiffness
related to its PSD. This term avoids a noise propagation and
amplification on the PSF (cf. Sect. 5) as well as the trivial solution (PSF = image and all the sources = 0
except one delta function).
This leads to a strong decrease of the number of parameters. In the case of a
![]() pixels image of a binary star, the number of parameters drops from
16384 (if the object parameters are the intensity on each pixel) to 6
(two intensities, two position vectors). It therefore allows
a better precision on these parameters; in particular, a
sub-pixel determination of star position -- meaning a fraction of
pixels image of a binary star, the number of parameters drops from
16384 (if the object parameters are the intensity on each pixel) to 6
(two intensities, two position vectors). It therefore allows
a better precision on these parameters; in particular, a
sub-pixel determination of star position -- meaning a fraction of
![]() for Shannon sampled images -- and an accurate photometry
measurement.
for Shannon sampled images -- and an accurate photometry
measurement.
Also, fewer parameters to estimate lead to a faster
convergence.
We now turn to the different ways of estimating the PSF and its associated PSD.
Copyright The European Southern Observatory (ESO)