One possibility to estimate the PSF, is to image a star near the observed object (Northcott 1996). This technique however presents some major problems: waste of observation time, small sky coverage, evolution of the turbulence between object and reference star acquisition.
Recently, a method has been
proposed to accurately retrieve the mean PSF (![]() ) from the data
accumulated by the AO control system during the acquisition
(Veran et al. 1997). This mean PSF however corresponds to an image with
an infinite integration time.
) from the data
accumulated by the AO control system during the acquisition
(Veran et al. 1997). This mean PSF however corresponds to an image with
an infinite integration time. ![]() is obtained using the theoretical expression:
is obtained using the theoretical expression:
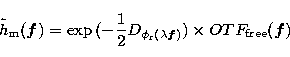 |
(6) |
![]() differs from the actual finite time PSF because of the
so-called turbulence noise, related to the residual speckles in the AO
corrected images. The shorter the integration time, the larger the turbulence noise. The variance of this noise on
the optical transfer function for an integration time
differs from the actual finite time PSF because of the
so-called turbulence noise, related to the residual speckles in the AO
corrected images. The shorter the integration time, the larger the turbulence noise. The variance of this noise on
the optical transfer function for an integration time ![]() can be estimated at each spatial frequency by (Conan 1994):
can be estimated at each spatial frequency by (Conan 1994):
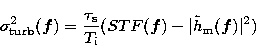 |
(7) |
The difficulty lies in the estimation of the
coherence time ![]() . It corresponds roughly to the turbulence
evolution time. Without AO correction,
. It corresponds roughly to the turbulence
evolution time. Without AO correction, ![]() is the so-called speckle
boiling time characterizing the speckle life time. An approximate value is given by Roddier
(Roddier et al. 1982). It could be
different in the case of AO correction and certainly depends on the correction
degree. However we assume, in a first approximation, that the expression given
by Roddier is valid here:
is the so-called speckle
boiling time characterizing the speckle life time. An approximate value is given by Roddier
(Roddier et al. 1982). It could be
different in the case of AO correction and certainly depends on the correction
degree. However we assume, in a first approximation, that the expression given
by Roddier is valid here:
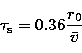 |
(8) |
With accurate models of the servo-loops, WFS, deformable mirror, a bright enough object, the error on the PSF estimated from the AO loop data is
dominated by the turbulence noise (Veran 1997). Therefore, we have:
| |
(9) |
Copyright The European Southern Observatory (ESO)