2 Cosmic ray impact suppression

 

2.1 Cosmic ray impacts

At first sight, the images from ISOCAM are crossed by strings of high value pixels produced by cosmic ray impacts. This is most apparent for the LW channel of ISOCAM as the LW detector is significantly thicker than the SW detector. Most of these glitches are due to mild, fast electron energy deposition along a string of pixels. Typically for the LW detector, on average, about 40 to 60 pixels are affected at any time for an integration time of 5 seconds. Those pixels usually recover completely after one or two readouts. However, some impacts can have long lasting effects (up to 5 minutes) on the hit pixel. They are thought to be due to heavy particles. There is one impact with this behavior about every second somewhere on the LW channel. The rate of cosmic ray impacts increases greatly when ISO is close to its perigee, due to the radiation belt.

Cosmic ray impact suppression (also called deglitching) is not a trivial task for several reasons. First of all the data are rarely fully stabilized (i.e. it takes a long time until the pixel reaches a stabilized value, although the incoming flux is constant) and this implies that not all differences between two successive frames can be attributed to cosmic ray impacts. Secondly, several glitches can hit the same pixel successively and create a long temporal structure which could be considered a source by a simple algorithm. The wavelet transform is not well adapted to treat this kind of data, due to the linearity of the transform. At a glitch position, a structure would be detected at all scales. This is due to the high intensity of the glitch. The Multiresolution Median Transform (MMT), proposed by Starck et al. (1996), is an alternative to the wavelet transform. It is a non-linear multiresolution transform, and is particularly useful every time we have structures with large dynamics. This is the case for the deglitching problem.

2.2 The multiresolution median transform

The median transform is nonlinear, and offers advantages for robust smoothing (i.e. the effects of outlier pixel values are mitigated). We define the median transform of a one dimensional signal S, with a window of dimension n, as med(S, n). Let n = 2l+1; initially l=1. The iteration counter is denoted by j, and $N\rm _s$ is the user-specified number of resolution scales.

1.

Let j=1, l=1, and c₁ = S.

2.

Determine c_j+1 = med(S, 2l+1).

3.

The multiresolution coefficients w_j are defined as: w_j = c_j - c_j+1.

4.

Let $j \longleftarrow j+1$; $l \longleftarrow 2l$. Return to Step 2 if $j < N\rm _s$.

A straightforward expansion formula for the original signal is given by:

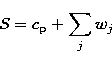$$S = c_{\rm p} + \sum_j w_j$$ (1)

where $c\rm _p$ is the residual signal.

In Step 3, the set of resolution levels associated with l leads to a dyadic analysis. Other possibilities involving intermediate scales (e.g. $l \longleftarrow 1.5l$) can also be considered.

The multiresolution coefficient values, w_j, are not necessarily of zero mean. Note that values of w_j can be negative.

For integer signal input values, this transform can be carried out in integer arithmetic alone which may lead to computational savings.

Computational requirements of the multiresolution transform are high, and these can be reduced by decimation: one pixel out of two is retained at each scale. Here the transform kernel does not change from one iteration to the next, but the signal to which this transform is applied does. This pyramidal algorithm is described in Starck et al. (1998).

2.3 Cosmic ray impact suppression

As the glitch structures can have different sizes, we need a multiresolution tool in order to perform efficient automatic detection. The idea developed here is the following: as we observe the same position in the sky during n exposures, we cannot have any structure in our signal which has a temporal size less than n*tint (tint being the exposure time of a single frame). It means that all the significant structures (i.e. not due to the noise) at small temporal scales are due to the glitches.

The method consists in doing for each pixel (x,y) the following steps, where D represents the raw data (three dimensional array)

1.

set S(t) = D(x,y,t)

2.

estimate the temporal noise $\rm \sigma_t$ in S(t) (see (Starck & Murtagh 1998) for more details on this step)

3.

calculate the MMT of S(t). The result is w_j(t) where j is the temporal scale. The number of scales in the transform is fixed due to the number of frames per satellite position.

4.

derive from $\rm \sigma_t$ the standard deviation $\sigma_j$ at each scale j.

5.

at all scales, set to zero all structures higher than a given level.

$$\begin{eqnarray} \mbox{ if } abs(w_j(t)) \gt k \sigma_j \mbox{ then } w_j(t) = 0\end{eqnarray}$$ (2)

k is generally taken equal to 4.

Figure 1 shows the results of such a treatment. Figure 1 (top) shows the values of a pixel of the camera as time elapses. The x-axis represents the frame number (time/integration time), and the y-axis is the signal in ADU per second. These data were collected during a raster observation, and the satellite remained at the same position for about 20 frames, and the integration time was equal to 2.1s. A source is at the limit of detection (frames 130 to 150). All peaks are due to cosmic ray impacts. The intensity of a cosmic ray can range all values between a few ADU to more than one thousand ADU (glitch detection limit depends on the noise level in the data). Figure 1 (middle) shows the same data after the glitch suppression. The third plot (Fig. 1 (bottom)) shows both data and deglitched data overplotted. We see that the noise and the signal are not modified during this operation.

  

Figure 1: Original data (top), deglitched data (middle), and both overplotted (bottom)

The method is robust and works for non-stabilized data. The only real limitation is that we cannot detect glitches which last for a time longer than or equal to n * tint. That means that the more frames we have per camera configuration, the better the deglitching will be. Some "special'' glitches introduce a gain variation with a very long time duration. These special glitches can be separated in two types: 1) the pixel value decreases slowly until a stabilized value is reached (see Fig. 2); 2) the pixel value decreases first below the stabilized value, and then increase slowly until the stabilized value is reached (see Fig. 3). In both cases, the stabilization can be very slow, and the deglitching method presented here does not correct for this effect. Finally, pixels where a glitch has been detected are not used when averaging values corresponding to the same sky position and same configuration.

The deglitching works separately on each pixel, and does not take into account the spatial information. In principle it should identically deglitch point sources and extended sources. However, in practice, differences are introduced by the spacecraft jitter, especially when using the 1.5'' and 3'' lenses. As jitter will slightly move point sources on the array, which exhibit strong brightness spatial gradients, this random motion creates artificial temporal variations similar to glitches on any pixel that sees the sources, although in these cases they correspond to real signal. Thus these variations are generally removed by the deglitching algorithms and the consequence is a systematic loss of flux for point sources. No automatic procedure currently exists to account for this artifact.

  

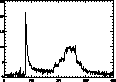Figure 2: Glitch with very long duration. The flux in ADU is plotted against time given by the exposure index

  

Figure 3: Glitch with a negative tail. The flux in ADU is plotted against time given by the exposure index. Note the gain variation of about 5 ADUs which appears after the second glitch