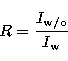Up: Present performance of the coronagraph
Subsections
The dark-speckle coronagraph (DSC) combines features of adaptive optics, Lyot
coronagraphy and speckle interferometry.
Figure 1 shows the arrangement utilized at the Coudé focus of the 152 cm
telescope
at
Observatoire de Haute-Provence.
The stellar beam from the
telescope enters the adaptive optics bench BOA, of the
ONERA
(Office National d'Études et de Recherches Aérospatiales). It has 88
actuators and responds fast enough for seeing correction in the visible range
(Conan et al. 1998).
Downstream from BOA, the afocal beam reaches a dichroic beamsplitter
which transmits the IR (K band) light towards another instrument used
simultaneously, the achromatic interfero-coronagraph
(Gay & Rabbia 1996), while
visible
light (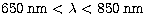 ) is reflected to the DSC.
) is reflected to the DSC.
|
Figure 1:
Dark speckle camera used at the Haute-Provence 1.52 m telescope (not
a scale drawing). The dichroic beam-splitter selects the wavelength range
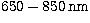 in reflection. The collimated beam received from the telescope with
BOA adaptive optics crosses a pair of Risley prisms for atmospheric dispersion
compensation and is focussed by concave
mirror CM onto the Lyot occulting mask OM. The masked field is re-imaged onto
photon-counting camera CP through the pair of Wynne corrector triplets WT
which compensate the first-order lateral chromatism of diffraction patterns.
A Lyot stop LS removes stellar diffracted light at the edge of the
relayed pupil, according to the classical Lyot coronagraph principle in reflection. The collimated beam received from the telescope with
BOA adaptive optics crosses a pair of Risley prisms for atmospheric dispersion
compensation and is focussed by concave
mirror CM onto the Lyot occulting mask OM. The masked field is re-imaged onto
photon-counting camera CP through the pair of Wynne corrector triplets WT
which compensate the first-order lateral chromatism of diffraction patterns.
A Lyot stop LS removes stellar diffracted light at the edge of the
relayed pupil, according to the classical Lyot coronagraph principle |
The Strehl ratio reached 10% to 30% depending on seeing conditions. Although
the adaptive optics gain is higher in the IR range, the advantage of working
with visible light results from the use of a photon-counting camera.
Its low dark count allows short exposures with negligible added noise, as
required for speckle observations.
The centering of the star's image on the Lyot occulting mask is critical,
and should be part of the adaptive optics loop. This is achievable by
collecting light reflected from the mask, but the drift had to be corrected
manually at this stage.
The diffraction rings are removed by a Lyot coronagraph (Lyot 1930,
Fig. 1).
The occulting masks in the f/122 beam
are inter-changeable, with sizes correponding to 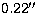 ,
,  and
and 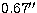 . They have been vaccum evaporated through
pinholes onto a 1.2 mm thick plate of anti-reflection coated glass. The
apodizing masks located at the relayed pupil are pinholes carried by a x-y
translation stage. No attempt was made to mask the aperture
spider and central obscuration although this
should decrease the scattered light significantly.
The atmospheric dispersion corrector, located near the first pupil image, uses
a pair of normal-field Risley prisms, which are rotated. The glasses,
Schott PK51A and Corning B29-52, correct a wide spectral bandpass, from
. They have been vaccum evaporated through
pinholes onto a 1.2 mm thick plate of anti-reflection coated glass. The
apodizing masks located at the relayed pupil are pinholes carried by a x-y
translation stage. No attempt was made to mask the aperture
spider and central obscuration although this
should decrease the scattered light significantly.
The atmospheric dispersion corrector, located near the first pupil image, uses
a pair of normal-field Risley prisms, which are rotated. The glasses,
Schott PK51A and Corning B29-52, correct a wide spectral bandpass, from
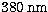 up to
up to 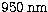 . The residual chromatism
in the
. The residual chromatism
in the 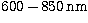 band is
on average 1/4 of the Airy peak diameter, corresponding to
band is
on average 1/4 of the Airy peak diameter, corresponding to 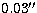 at
at 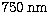 . With the 1.5 m telescope and the 6mm pupil, the prisms correct up
to
. With the 1.5 m telescope and the 6mm pupil, the prisms correct up
to 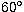 from zenith. We adjusted visually the prism settings although
pre-calculated settings would be preferable,
especially for faint stars.
For conventional speckle interferometry the detected bandwidth can be
increased by transforming the partially proportional wavelength dependence
of the speckle scale.
Here, the proportionality is more
accurate since the residual phase on the wave is made small
by the adaptive optics. The photon rate being critical in ground-based
dark-speckle imaging, there is much to gain in increasing the usable
spectral bandwidth.
from zenith. We adjusted visually the prism settings although
pre-calculated settings would be preferable,
especially for faint stars.
For conventional speckle interferometry the detected bandwidth can be
increased by transforming the partially proportional wavelength dependence
of the speckle scale.
Here, the proportionality is more
accurate since the residual phase on the wave is made small
by the adaptive optics. The photon rate being critical in ground-based
dark-speckle imaging, there is much to gain in increasing the usable
spectral bandwidth.
|
Figure 2:
Wynne corrector for making the speckle pattern wavelength-invariant.
A
pair of
triplets,
afocal in yellow light, shrinks the blue pupil
while enlarging the red pupil. The exit angle, u',
becomes approximately proportional to wavelength, thus ensuring a nearly
wavelength-invariant diffraction pattern |
One of us (DK) has re-calculated the corrector solution
obtained by Wynne (1979) (Fig. 2). The pair of null triplets
shrinks the blue pupil, while enlarging the red pupil, so that both Airy
patterns, or speckle patterns, are of nearly identical
size. With respect to the original Wynne design, we have suppressed the
power in the second triplet, in order to keep more
flexibility in the final magnification and we have replaced the SF8 glass
by SFL5 for optimal correction in the red range (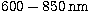 ).
).
- At
 , the glasses have the same refractive index
and the two triplets behave as two plane-parallel plates.
, the glasses have the same refractive index
and the two triplets behave as two plane-parallel plates.
- System performance is limited by the non-linearity of the glass
dispersion. In the range
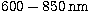 , the final radial
chromatism, including diffraction, is lower than 1.7%
of the axial distance
(Fig. 6).
, the final radial
chromatism, including diffraction, is lower than 1.7%
of the axial distance
(Fig. 6).
- The corrected field is quite small owing to the strong curvatures which
limit the diameter of the exit triplet.
- The star image must be kept on axis, and any companion has its Airy peak
dispersed,
although not very much with the
small relative spectral bandwidth utilized. Field spectrocopy techniques
(Bacon et al. 1995) or wavelength sensitive detectors such as the
Super-conductive Tunnel Junction camera (Peacok et al. 1998) could solve this residual
problem.
- Although it would be nice to insert the occulting mask in the achromatised
image, the following pupil would become
chromatic, which would complicate the apodization masking.
The analytical derivation is given in Appendix.
Finally L2 focuses the beam onto the camera with an 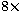 magnification,
bringing the aperture to f/976.
magnification,
bringing the aperture to f/976.
The detector is a cooled CP20 photon-counting camera (Vakili 1990) having a
first-generation electrostatic intensifier coupled to a second-generation
microchannel intensifier and a fiber optics taper, feeding a 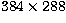 CCD. The resulting amplification is about 105. Such a device allows single
photon detection and a very low dark count,
less than 10 photons per
CCD. The resulting amplification is about 105. Such a device allows single
photon detection and a very low dark count,
less than 10 photons per  exposure for
exposure for 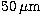 pixels at
pixels at
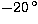 C
(about 0.0045 photons/s/pixel). A low dark
noise is necessary to detect accurately any "filling'' of the dark speckles,
which could reveal the presence of a faint
companion. The
drawbacks of such photon-counting cameras are their low quantum efficiency
(
C
(about 0.0045 photons/s/pixel). A low dark
noise is necessary to detect accurately any "filling'' of the dark speckles,
which could reveal the presence of a faint
companion. The
drawbacks of such photon-counting cameras are their low quantum efficiency
(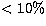 at
at 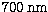 ) and their low saturation
level of
) and their low saturation
level of 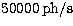 , limited by the
acquisition system.
, limited by the
acquisition system.
As mentioned above, the coronagraph forms a f/976 focus on the detector in
order to achieve the dense sampling required by the dark-speckle technique.
For a central wavelength of 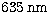 ,
it represents 150 pixels/speckle area or 144 pixels/arcsecond. The field
of view is limited to a diameter of 250
pixels (about
,
it represents 150 pixels/speckle area or 144 pixels/arcsecond. The field
of view is limited to a diameter of 250
pixels (about 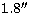 ) by the Wynne corrector. In addition to the Wynne
corrector, spectral filters can be inserted
in front of the photocathode to select different narrow bandwidths.
) by the Wynne corrector. In addition to the Wynne
corrector, spectral filters can be inserted
in front of the photocathode to select different narrow bandwidths.
 |
Figure 3:
a) Reference image obtained
with a white light source inside the BOA adaptive optics system, using
the  mask and without the Lyot stop. The Airy rings remain
visible. Diffraction spikes from the spider arms can be seen as dotted lines,
influenced by the ring structure.
In such conditions a planetary companion would be invisible.
In spite of the broad spectral bandwidth ( mask and without the Lyot stop. The Airy rings remain
visible. Diffraction spikes from the spider arms can be seen as dotted lines,
influenced by the ring structure.
In such conditions a planetary companion would be invisible.
In spite of the broad spectral bandwidth ( )
at )
at  , the outer rings retain good contrast,
owing to the Wynne corrector , the outer rings retain good contrast,
owing to the Wynne corrector |
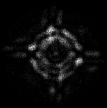 |
Figure 3:
b) The same reference frame
obtained with the mask and the  Lyot stop. Here, the Airy pattern
is markedly attenuated and the gain in sensitivity is about 1.7 magnitudes.
Nevertheless, due to the inadapted Lyot stop, some bright features remain,
like the rings around the mask and the four symmetrical speckles which could
bring out wrong detections. These static defects can be partially removed
with frame subtraction Lyot stop. Here, the Airy pattern
is markedly attenuated and the gain in sensitivity is about 1.7 magnitudes.
Nevertheless, due to the inadapted Lyot stop, some bright features remain,
like the rings around the mask and the four symmetrical speckles which could
bring out wrong detections. These static defects can be partially removed
with frame subtraction |
To calibrate the efficiency of the Lyot stop, we have acquired
an internally-generated reference image
using a single-mode fiber included in BOA. The Strehl ratio (SR) of this
reference source is about 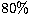 and does not take into account the
atmospheric turbulence or the static aberrations of the adaptive mirror.
When the core of the Airy pattern is occulted by the mask, the edges of the
pupil image become decorated with two bright fringes (Fig. 1). The
complementary spatial filter in the pupil plane should suppress much
of the diffracted light, except that caused by the wave bumpiness.
The Lyot stop being a simple pinhole of
and does not take into account the
atmospheric turbulence or the static aberrations of the adaptive mirror.
When the core of the Airy pattern is occulted by the mask, the edges of the
pupil image become decorated with two bright fringes (Fig. 1). The
complementary spatial filter in the pupil plane should suppress much
of the diffracted light, except that caused by the wave bumpiness.
The Lyot stop being a simple pinhole of
 instead of a telescope pupil image, some Airy-like
rings remain visible in the final image (Fig. 3b). Moreover, the spider
spikes combined with the residual rings produce symmetrical side-lobes,
especially
bright within the 2 first rings. These artifacts remain on the compensated
images despite the smoothing introduced by the atmospheric turbulence.
instead of a telescope pupil image, some Airy-like
rings remain visible in the final image (Fig. 3b). Moreover, the spider
spikes combined with the residual rings produce symmetrical side-lobes,
especially
bright within the 2 first rings. These artifacts remain on the compensated
images despite the smoothing introduced by the atmospheric turbulence.
One can compute the rejection rate of the coronagraph
as defined in Malbet 1996:
| 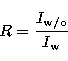 |
(1) |
where 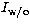 is the total intensity of the reference beam without
coronagraph and
is the total intensity of the reference beam without
coronagraph and 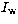 is its intensity with the coronagraph. To
characterize the efficiency of the Lyot stop, one defines
is its intensity with the coronagraph. To
characterize the efficiency of the Lyot stop, one defines
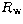 the rejection
rate with the Lyot stop and
the rejection
rate with the Lyot stop and 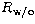 without it.
We can then estimate the
gain in magnitude introduced by the Lyot stop with the following relation
(Malbet 1996):
without it.
We can then estimate the
gain in magnitude introduced by the Lyot stop with the following relation
(Malbet 1996):
| 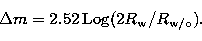 |
(2) |
A gain of 1.7 magnitude has been measured for the  mask and
the
mask and
the  Lyot stop. As this value is averaged over the entire field, it
is therefore underestimated far from the axis and overestimated near the mask.
An optimized Lyot stop, including secondary mirror and spider arms, should
improve the gain by another 1.3 magnitude (Malbet 1996).
Lyot stop. As this value is averaged over the entire field, it
is therefore underestimated far from the axis and overestimated near the mask.
An optimized Lyot stop, including secondary mirror and spider arms, should
improve the gain by another 1.3 magnitude (Malbet 1996).


Up: Present performance of the coronagraph
Copyright The European Southern Observatory (ESO)
![]() CCD. The resulting amplification is about 105. Such a device allows single
photon detection and a very low dark count,
less than 10 photons per
CCD. The resulting amplification is about 105. Such a device allows single
photon detection and a very low dark count,
less than 10 photons per ![]() exposure for
exposure for ![]() pixels at
pixels at
![]() C
(about 0.0045 photons/s/pixel). A low dark
noise is necessary to detect accurately any "filling'' of the dark speckles,
which could reveal the presence of a faint
companion. The
drawbacks of such photon-counting cameras are their low quantum efficiency
(
C
(about 0.0045 photons/s/pixel). A low dark
noise is necessary to detect accurately any "filling'' of the dark speckles,
which could reveal the presence of a faint
companion. The
drawbacks of such photon-counting cameras are their low quantum efficiency
(![]() at
at ![]() ) and their low saturation
level of
) and their low saturation
level of ![]() , limited by the
acquisition system.
, limited by the
acquisition system.
![]() ,
it represents 150 pixels/speckle area or 144 pixels/arcsecond. The field
of view is limited to a diameter of 250
pixels (about
,
it represents 150 pixels/speckle area or 144 pixels/arcsecond. The field
of view is limited to a diameter of 250
pixels (about ![]() ) by the Wynne corrector. In addition to the Wynne
corrector, spectral filters can be inserted
in front of the photocathode to select different narrow bandwidths.
) by the Wynne corrector. In addition to the Wynne
corrector, spectral filters can be inserted
in front of the photocathode to select different narrow bandwidths.