

Up: Present performance of the coronagraph
Subsections
A malfunction in the camera control computer caused the loss of
80% to 90% of the short exposures.
As a consequence, the speckle noise remains 3 times more intense than expected
and dominates the photon noise.
The dark-speckle algorithm is described in Labeyrie (1995)
and Boccaletti et al. (1998). The
data reduction software provides two images. The first is equivalent to a
long exposure, computed by co-adding all the short exposures containing the
position of the photon-events. The second image, called the "cleaned map'',
displays the result of the dark-speckle algorithm. The number of zero-photon
events occurring in binned pixels containing  camera pixels, is cumulated
over successive frames. The cleaned map, thus obtained in negative form,
can be inverted with a suitable gamma exponent.
In principle, the cleaned image
is more sensitive to the faint structures than the conventional long exposure.
camera pixels, is cumulated
over successive frames. The cleaned map, thus obtained in negative form,
can be inverted with a suitable gamma exponent.
In principle, the cleaned image
is more sensitive to the faint structures than the conventional long exposure.
Photon-counting data are affected by the so-called photon-centroiding
(Tiébaut 1994) resulting from the limited resolution of the electronics in space
and
time.
The counting behaviour is expected to improve with forthcoming detectors.
The signal to noise ratio (SNR) is measured in the cleaned map according to
Eq. (6) from Labeyrie (1995). The
magnitude difference is derived from the CP20 long exposure by comparing the
flux of the star outside the mask, and the flux of the companion when
the star is under the mask.
To assess the performance of the system, one can compute the expected maximum
brightness ratio theoretically reachable (Eq. (7) Boccaletti et al. 1998). This value
only depends on the sampling (150 pixels/speckle area) and on the adaptive
optics (AO) gain which is the brightness ratio between the peak of
the corrected image and the halo level.
The average AO gain obtained in the present run is about 15 at  from the star. The total
integration time is assumed to be very large compared to the speckle lifetime.
This leads to a 8.8
magnitude difference. However, as described in Sects. 3.2 and
3.3, this goal, although
modest with respect to the
from the star. The total
integration time is assumed to be very large compared to the speckle lifetime.
This leads to a 8.8
magnitude difference. However, as described in Sects. 3.2 and
3.3, this goal, although
modest with respect to the  goal attainable in principle with
future adaptive optics, was not reached
owing to practical problems. Among these was the loss of 90% of the
observing data, due to a computer failure.
goal attainable in principle with
future adaptive optics, was not reached
owing to practical problems. Among these was the loss of 90% of the
observing data, due to a computer failure.
 |
Figure 4:
a) Negative cleaned image of
the binary star  Per, obtained in H Per, obtained in H ( ( , ,
 ) with the ) with the  mask. The intensity of
the image represents the number
of zero photon collected with 9503 short exposures of mask. The intensity of
the image represents the number
of zero photon collected with 9503 short exposures of  . The hypothetic
companion (arrow) is visible at
the edge of the mask ( . The hypothetic
companion (arrow) is visible at
the edge of the mask ( , ,  ) as a "hole'' in the
cleaned map, amidst the fixed speckles generated by the spider structure.
At this location, the zero photon-count is lower than elsewhere ) as a "hole'' in the
cleaned map, amidst the fixed speckles generated by the spider structure.
At this location, the zero photon-count is lower than elsewhere |
 |
Figure 4:
b) The same image
enhanced with an inverse square law,
and smoothed to the speckle scale with a wavelet transform filter.
The faint companion ( ) emerges above the speckle noise,
although no reference star was available in this case to subtract the
fixed speckles ) emerges above the speckle noise,
although no reference star was available in this case to subtract the
fixed speckles |
The first target star observed is  Per (HD22928, mv=2.99,
Per (HD22928, mv=2.99,
 ), a binary system previously observed by Hipparcos
(ESA 1997). We used the
), a binary system previously observed by Hipparcos
(ESA 1997). We used the  occulting
mask and
occulting
mask and  pupil
stop. The turbulence conditions were characterized by r0= 8 cm during
observation. 9503 short exposures of
pupil
stop. The turbulence conditions were characterized by r0= 8 cm during
observation. 9503 short exposures of  Per have been acquired,
corresponding to an observing time of 190s. We used an
Per have been acquired,
corresponding to an observing time of 190s. We used an  filter
(
filter
( ) of bandwidth
) of bandwidth  . The faint companion appears at
. The faint companion appears at
 and
and  . The sampling on the
camera is 144 pixels per arcsecond.
The image (Figs. 4a
and 4b) presents
some fixed patterns, mainly produced by the spider arm diffraction which is
visible as four symmetrical bright speckles. An AO gain of 6, azimuthally
averaged, is obtained at
. The sampling on the
camera is 144 pixels per arcsecond.
The image (Figs. 4a
and 4b) presents
some fixed patterns, mainly produced by the spider arm diffraction which is
visible as four symmetrical bright speckles. An AO gain of 6, azimuthally
averaged, is obtained at  from the star. An SNR of 53 is
measured on the speckle size (
from the star. An SNR of 53 is
measured on the speckle size ( pixels), while the model
predicted an SNR of 133 (Boccaletti et al. 1998). The discrepancy with theory can be
an indirect effect of the computer failure mentioned above; speckle noise
becomes dominant owing to the small number of exposures.
The intensity of the companion was derived from the CP20 long exposure and
corresponds
to a
pixels), while the model
predicted an SNR of 133 (Boccaletti et al. 1998). The discrepancy with theory can be
an indirect effect of the computer failure mentioned above; speckle noise
becomes dominant owing to the small number of exposures.
The intensity of the companion was derived from the CP20 long exposure and
corresponds
to a 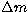 of
of  .The second target star,
.The second target star,  Psc (HD 9270, mv = 3.61, JD = 50730.507),
was also selected from the Hipparcos binary star catalogue.
Coronagraphic images of
Psc (HD 9270, mv = 3.61, JD = 50730.507),
was also selected from the Hipparcos binary star catalogue.
Coronagraphic images of  Psc were recorded without spectral
filter, the bandpass being limited by the
dichroic beam-splitter and the camera (
Psc were recorded without spectral
filter, the bandpass being limited by the
dichroic beam-splitter and the camera ( ). These images
illustrate the problem of the speckle
noise in the search for faint companions.
The Hipparcos data gives
). These images
illustrate the problem of the speckle
noise in the search for faint companions.
The Hipparcos data gives  ,
,  and
and
 ,
which is in good agreement with our results.
The second target star,
,
which is in good agreement with our results.
The second target star,  Psc (HD 9270, mv=3.61, JD = 50730.507),
was also selected from the Hipparcos binary star catalogue.
Coronagraphic images of
Psc (HD 9270, mv=3.61, JD = 50730.507),
was also selected from the Hipparcos binary star catalogue.
Coronagraphic images of  Psc were recorded without spectral
filter, the bandpass being limited by the
dichroic beam-splitter and the camera (
Psc were recorded without spectral
filter, the bandpass being limited by the
dichroic beam-splitter and the camera ( nm). These images
illustrate the problem of the speckle
noise in the search for faint companions.
Indeed, for the same reason as
above the number of short exposures is poor (9013). Altough the
companion emerges easily above the photon noise, the residual speckle noise
inhibits its detection on the raw data (Fig. 5a).
However, a nearby reference star (
nm). These images
illustrate the problem of the speckle
noise in the search for faint companions.
Indeed, for the same reason as
above the number of short exposures is poor (9013). Altough the
companion emerges easily above the photon noise, the residual speckle noise
inhibits its detection on the raw data (Fig. 5a).
However, a nearby reference star ( And, mv = 4.42), has been
observed immediately
afterwards for map subtraction (Fig. 5b). The efficiency of the
subtraction is limited for several reasons:
And, mv = 4.42), has been
observed immediately
afterwards for map subtraction (Fig. 5b). The efficiency of the
subtraction is limited for several reasons:
- (i)
- The conditions of turbulence, and thus the correction
applied by the AO system, are different for
both stars (
 for
for  And, and
And, and  for
for  Psc).
Psc).
- (ii)
- The coronagraphic images are not invariant to
translation (Malbet 1996), and in fact highly sensitive to tracking drift.
Any centering difference between both sequences causes spurious speckle
noise in the subtracted image.
- (iii)
- A 76 Hz vibration of the telescope drive motor, seen by the
Shack-Hartmann wave sensor, is left uncorrected by the adaptive system.
To overcome these problems, both star and reference have been corrected from
Flat-Field and smoothed with wavelet transform.
Then, to account for the lower speckle contrast of  Psc,
presumably caused by unequal seeing lifetime during both observations,
the reference star was convolved with a gaussian shape of 4 pixels width.
Finally,
Psc,
presumably caused by unequal seeing lifetime during both observations,
the reference star was convolved with a gaussian shape of 4 pixels width.
Finally,  And was shifted to overlap
And was shifted to overlap  Psc in the field, and
scaled in intensity (Fig. 5c). After subtraction
of the two cleaned negative images, the remaining bright and dark
speckles belong respectively to the reference star
(
Psc in the field, and
scaled in intensity (Fig. 5c). After subtraction
of the two cleaned negative images, the remaining bright and dark
speckles belong respectively to the reference star
( And) and the target star (
And) and the target star ( Psc).
Psc).
The measurement of the SNR, on the cleaned map, is made difficult by the
crowded
field.
Although the companion remains undetected on the initial image
(Fig. 5a),
in terms of speckle noise,
the comparison of both images eliminates all features common to
the target (Fig. 5a) and the reference
(Fig. 5b), so that the only
residual speckle indicates the
companion position ( ,
,  ).
This process leads to an SNR of 137,
instead of 250 as predicted by the model. In this case, the
SNR is naturally decreased by the companion's
smearing, induced by the Wynne correctors.
).
This process leads to an SNR of 137,
instead of 250 as predicted by the model. In this case, the
SNR is naturally decreased by the companion's
smearing, induced by the Wynne correctors.
The long exposure allows to derive a  in the R band.
The Hipparcos V-band data gives
in the R band.
The Hipparcos V-band data gives  ,
,  and
and
 . A difference of spectral types for both components can explain
the apparent discrepancy. We must also notice a discrepancy
in the companion position. As the orbital solution is unknown, further
observing runs will be needed to confirm
the detection of the companion.
. A difference of spectral types for both components can explain
the apparent discrepancy. We must also notice a discrepancy
in the companion position. As the orbital solution is unknown, further
observing runs will be needed to confirm
the detection of the companion.
 |
Figure 5:
a) Negative cleaned map of the
binary
star
 Psc, observed
with the Psc, observed
with the  mask and the Wynne corrector's spectral band
( mask and the Wynne corrector's spectral band
( , ,
 ). Due to the strong turbulence ( ). Due to the strong turbulence ( ) and the small number of
exposures (9013), the faint companion (arrow)
remains
buried
among the speckles. A flat field correction has been applied to the map ) and the small number of
exposures (9013), the faint companion (arrow)
remains
buried
among the speckles. A flat field correction has been applied to the map |
 |
Figure 5:
b) Reference star ( And)
observed in the same way just before And)
observed in the same way just before  Psc with r0 = 8 cm, 3645
short exposures. The suspected "companion" peak of
Fig. 5a is here absent,
although the static residual speckles are
similar. The scattered halo level is significantly lower than in
Fig. 4a Psc with r0 = 8 cm, 3645
short exposures. The suspected "companion" peak of
Fig. 5a is here absent,
although the static residual speckles are
similar. The scattered halo level is significantly lower than in
Fig. 4a
|
 |
Figure 5:
c) Difference of  Psc
and Psc
and  And cleaned maps.
The companion now appears as a dark feature (arrow). The image has been smoothed
with a wavelet transform filter And cleaned maps.
The companion now appears as a dark feature (arrow). The image has been smoothed
with a wavelet transform filter |
 |
Figure 5:
d)
Positive cleaned image obtained with
an inverse square law, and a threshold at 3 level level |
Table 1:
Summary of our results compared to the HIC data
|
|


Up: Present performance of the coronagraph
Copyright The European Southern Observatory (ESO)
![]() camera pixels, is cumulated
over successive frames. The cleaned map, thus obtained in negative form,
can be inverted with a suitable gamma exponent.
In principle, the cleaned image
is more sensitive to the faint structures than the conventional long exposure.
camera pixels, is cumulated
over successive frames. The cleaned map, thus obtained in negative form,
can be inverted with a suitable gamma exponent.
In principle, the cleaned image
is more sensitive to the faint structures than the conventional long exposure.
![]() from the star. The total
integration time is assumed to be very large compared to the speckle lifetime.
This leads to a 8.8
magnitude difference. However, as described in Sects. 3.2 and
3.3, this goal, although
modest with respect to the
from the star. The total
integration time is assumed to be very large compared to the speckle lifetime.
This leads to a 8.8
magnitude difference. However, as described in Sects. 3.2 and
3.3, this goal, although
modest with respect to the ![]() goal attainable in principle with
future adaptive optics, was not reached
owing to practical problems. Among these was the loss of 90% of the
observing data, due to a computer failure.
goal attainable in principle with
future adaptive optics, was not reached
owing to practical problems. Among these was the loss of 90% of the
observing data, due to a computer failure.
![]() Psc,
presumably caused by unequal seeing lifetime during both observations,
the reference star was convolved with a gaussian shape of 4 pixels width.
Finally,
Psc,
presumably caused by unequal seeing lifetime during both observations,
the reference star was convolved with a gaussian shape of 4 pixels width.
Finally, ![]() And was shifted to overlap
And was shifted to overlap ![]() Psc in the field, and
scaled in intensity (Fig. 5c). After subtraction
of the two cleaned negative images, the remaining bright and dark
speckles belong respectively to the reference star
(
Psc in the field, and
scaled in intensity (Fig. 5c). After subtraction
of the two cleaned negative images, the remaining bright and dark
speckles belong respectively to the reference star
(![]() And) and the target star (
And) and the target star (![]() Psc).
Psc).
![]() ,
, ![]() ).
This process leads to an SNR of 137,
instead of 250 as predicted by the model. In this case, the
SNR is naturally decreased by the companion's
smearing, induced by the Wynne correctors.
).
This process leads to an SNR of 137,
instead of 250 as predicted by the model. In this case, the
SNR is naturally decreased by the companion's
smearing, induced by the Wynne correctors.
![]() in the R band.
The Hipparcos V-band data gives
in the R band.
The Hipparcos V-band data gives ![]() ,
, ![]() and
and
![]() . A difference of spectral types for both components can explain
the apparent discrepancy. We must also notice a discrepancy
in the companion position. As the orbital solution is unknown, further
observing runs will be needed to confirm
the detection of the companion.
. A difference of spectral types for both components can explain
the apparent discrepancy. We must also notice a discrepancy
in the companion position. As the orbital solution is unknown, further
observing runs will be needed to confirm
the detection of the companion.

