The approximations employed in this algorithm are valid for accurate work in many applications, but there are certain classes of orbit for which the approximations break down and may lead to inaccurate results.
First, and perhaps most importantly, the algorithm assumes a
fixed inclination between the two orbital planes. In reality, the angle
![]() changes with time and this results in a change of the mutual
inclination
changes with time and this results in a change of the mutual
inclination ![]() .
.
In order to deal with this we repeatedly use the fixed plane algorithm
and integrate across the distribution of ![]() produced by the
variations of
produced by the
variations of ![]() and
and ![]() . The integration is carried out
over the variable
. The integration is carried out
over the variable ![]() , the difference between
, the difference between ![]() and
and
![]() , using standard one-dimensional methods over the interval
, using standard one-dimensional methods over the interval
![]() .
.
It is easy to show that ![]() is a simple function of
is a simple function of
![]() such that
such that
| |
(20) |
Taking this into account, it becomes possible to cover the vast majority of orbits, but there remain small regions of configuration space where the algorithm breaks down due to geometric singularities. These singularities do not exist in the real system and arise only as a result of the simplified encounter geometry, namely the approximation of rectilinear relative motion during the close encounter.
The algorithm assumes that the elements a, e and i are so slowly varying that they can be assumed to be constant over timescales of interest. In some instances this may not be the case, particularly if the objects are affected by secular perturbations that significantly affect (for example) the eccentricity and inclination, even in cases when the semi-major axis is approximately constant. The point has been discussed by Davis et al. (1992), and in principle such variations could be accommodated within the present algorithm by adding further layers of integration to the model. However, this removes the virtues of simplicity and speed from the model, and would require a more complete dynamical representation of the system. If exact results are required in particular cases, then it may be necessary to return to a computer-intensive numerical integration scheme.
It is likely that in any application involving a large number of test bodies some pairs of orbits will lie sufficiently close to singular regions to produce unrealistic results. Singularities are also encountered with other methods, since they are implicit in the assumptions on which the algorithm is based.
Inaccurate results will be produced by pairs of orbits with low relative
inclinations, and indeed Öpik suggested that his theory was inadequate
for inclinations ![]() . The value of
. The value of ![]() approaches
infinity, at least as evaluated by the simple equations, since as
approaches
infinity, at least as evaluated by the simple equations, since as ![]() approaches zero it becomes impossible to separate the orbits by
rotating them around the origin. Examination of the conditions makes it
clear that the maximum value of
approaches zero it becomes impossible to separate the orbits by
rotating them around the origin. Examination of the conditions makes it
clear that the maximum value of ![]() should be smaller than
the size of the phase space over which we are integrating.
should be smaller than
the size of the phase space over which we are integrating.
The simplest way to prevent this is to ensure that the relative
inclination used during the integration is never less than some critical
value. The adjustment of the relative inclination should be performed on
the inclinations of the input orbits, rather than by limiting ![]() ,shifting the values of i1 and i2 such that
Eq. (20) will give a value higher than our enforced limit
for all values of
,shifting the values of i1 and i2 such that
Eq. (20) will give a value higher than our enforced limit
for all values of ![]() .
.
Similarly, problems occur when the perihelia or aphelia of either
orbit coincide, since for such orbits the separation parameter
![]() at this point and therefore
at this point and therefore ![]() diverges. This is a direct result of approximating the curved
trajectories in space at the close encounter by straight lines. For
orbits with configurations sufficiently close to this singularity
condition the results will be inaccurate.
diverges. This is a direct result of approximating the curved
trajectories in space at the close encounter by straight lines. For
orbits with configurations sufficiently close to this singularity
condition the results will be inaccurate.
In the version of the code implemented by the authors these singularities are dealt with by interpolating across the region where the singularity is known to exist. Orbits with q or Q sufficiently close to the Q or q of the other have probabilities computed by taking variations of each orbit with slightly differing elements, the magnitude of these variations being chosen to be comparable to the short-term variations in the orbital elements introduced by ordinary planetary perturbations. In practical applications we have found that such an approach produces reasonable results.
We emphasize that these singularities, arising from nearly coplanar or tangent orbits, are unphysical, in the sense (as proved by Wetherill 1967) that the corresponding collision integrals are always finite and can in principle be evaluated using other methods. One way of dealing with them is to use a more appropriate numerical integration technique, as was implemented by Farinella & Davis (1992); another, involving a suitable change of coordinates to remove the improper integral, has been discussed by Milani et al. (1990). In either case, owing to orbital evolution, the singularities are only short-lived, and the method of handling them has to be considered in relation to the physics of the dynamical system.
The present algorithm assumes that the orbits sample
![]() -space uniformly. It is difficult to provide
simple rules to determine whether a pair of orbits satisfies this
criterion adequately. For example, both orbits may be in resonances,
leading the orbit pairs to have strongly correlated elements. Such orbits
may only explore certain regions of phase space, along specific paths,
and we can no longer logically assume that every point in
-space uniformly. It is difficult to provide
simple rules to determine whether a pair of orbits satisfies this
criterion adequately. For example, both orbits may be in resonances,
leading the orbit pairs to have strongly correlated elements. Such orbits
may only explore certain regions of phase space, along specific paths,
and we can no longer logically assume that every point in
![]() -space is equally likely. Obviously, for every
pair of orbits the evolution of
-space is equally likely. Obviously, for every
pair of orbits the evolution of ![]() and
and ![]() can in
principle be determined, but good pairs will explore most of
can in
principle be determined, but good pairs will explore most of
![]() -space uniformly. The approximation to this
behaviour is that every point in
-space uniformly. The approximation to this
behaviour is that every point in ![]() -space is
equally weighted, as too are the points on the curve of intersection.
Unfortunately, the most straightforward way to avoid these difficulties
is through a direct numerical integration of the problem orbits, which of
course is computationally expensive and is what this and similar methods
have been designed to avoid.
-space is
equally weighted, as too are the points on the curve of intersection.
Unfortunately, the most straightforward way to avoid these difficulties
is through a direct numerical integration of the problem orbits, which of
course is computationally expensive and is what this and similar methods
have been designed to avoid.
The algorithm assumes fixed target radii, but if the bodies have
sufficient mass then the effective target area will be a function of
their relative velocity, owing to their mutual gravitational
attraction. For spherical targets with a combined mass M=M1 +M2
and radius of interaction R=R1+R2 the effective cross section,
![]() can be calculated from
can be calculated from
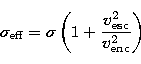 |
(21) |
We note that both P (proportional to ![]() ) and
) and ![]() are proportional to R, so the resulting collision probability is
proportional to R2 and therefore proportional to
are proportional to R, so the resulting collision probability is
proportional to R2 and therefore proportional to ![]() .
.
Copyright The European Southern Observatory (ESO)