4 Tests and results

This algorithm was designed to calculate efficiently the collision probability per unit time between objects moving in arbitrary elliptical orbits. The algorithm has been tested in a variety of ways and against a number of previous results. 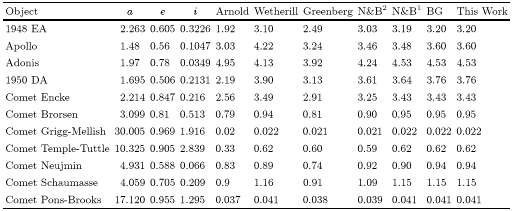First we compare our results with those of Wetherill (1967) and subsequent workers, who have determined the intrinsic collision probability between a number of selected comets and asteroids against a hypothetical test body, Astrid', with orbital elements $(a,e,i) = (2.75\,\mbox{AU}, 0.2727, 0.2760\,\mbox{(rads)})$.The results are shown in Table 1, which shows excellent agreement with the independent results of Namiki & Binzel (1991) and Bottke & Greenberg (1993), denoted N&B¹, N&B² and BG respectively.

  

Table 1: Comparison between the total collision probabilities per unit time between various bodies, determined by previous authors and this work. The values refer to encounters between real objects and the hypothetical test body, Astrid, considered by Arnold (1965), Wetherill (1967), and Greenberg (1982). The orbital elements of Astrid are (a,e,i) = (2.75, 0.2727, 0.2760), and in evaluating the total collision probability we have assumed a combined interaction radius $R=1\,$km, corresponding to a geometric cross-section for collision $\sigma = \pi$km². We emphasize that this fictitious body has no relation to the real asteroid (1128)Astrid. The tabulated values ignore gravitational focusing, and are given in units of $10^{-18}\,$yr^-1. The columns denoted N&B² and N&B¹ (from Namiki & Binzel 1991) refer to results from their model in which Astrid is taken to be the test particle and field particle respectively; the difference between these columns provides an indication of the relative accuracy of their results

  

Table 2: Impact probabilities between representative near-Earth asteroids and the Earth, per billion years, taken from Steel & Baggaley (1985), compared with results from this paper

  

Table 3: Impact probabilities between representative Earth-crossing comets and the Earth taken from Olsson-Steel (1985) and comparison with this paper. The Olsson-Steel results are given in units per billion orbits and per billion years respectively, and those from this paper are in units per billion years. Note that the orbital elements are those used by Olsson-Steel

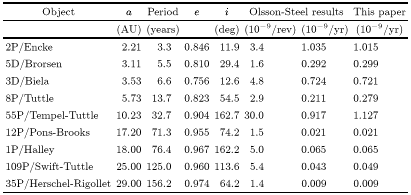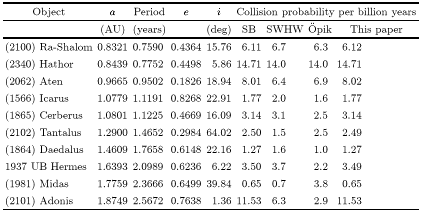
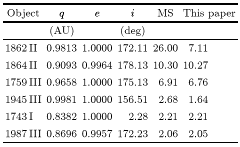
Next we evaluated the impact probabilities of selected objects with the Earth. Table 2 shows the comparison between a number of Apollo and Aten asteroids, with orbital elements and other data from Shoemaker et al. (1979) and results from the Öpik method taken from Steel & Baggaley (1985). Table 3 gives corresponding results for comets, taken from Olsson-Steel (1987), and Table 4 shows the equivalent comparison for long-period comets with extremely high impact probabilities, with elements taken from Marsden & Steel (1994).

These results are also in good agreement with those of previous authors, with several notable exceptions, namely: (2101)Adonis (Table 2), 1862II = C/1862N1 and 1945III = C/1945L1 (Table 4). The first of these is close to a singularity at low inclination; the second and third have perihelion distances close to that of the Earth. As we have discussed, most methods for evaluating the collision probability experience singularities at very low and very high relative inclinations, and when either the perihelion or aphelion of one orbit is in close proximity to those points in the other orbit. These minor differences show that further work is required in order to determine the precise value of the impact probability for some of these more extreme cases.

We have confirmed that the mean terrestrial impact probability p_E for an isotropic flux of nearly parabolic orbits with perihelion distances uniformly distributed in the interval 0-1AU is $2.18\ 10^{-9}$per revolution (cf. Weissman 1997 and refs. therein), with a mean impact velocity including gravitational focusing of 54.9km s^-1. Alternative expressions for the frequency distribution of long-period comets versus perihelion distance (Everhart 1967; Kresák 1978) generally show an increase with perihelion distance. This leads to a higher average terrestrial impact probability, namely: $(2.46,2.36,2.50)\ 10^{-9}$ per revolution, for what Kresák (1978) respectively calls Everhart's empirical and alternative models, and Kresák's uniform density model. The observed long-period comets, whilst not necessarily representative of the intrinsic near-parabolic flux, show an even stronger increase with perihelion distance towards 1AU, and give a mean impact probability of $3.3\ 10^{-9}$ per revolution (cf. Shoemaker 1984; Olsson-Steel 1987).

  

Table 4: Selected long-period comets with high impact probabilities with respect to the Earth and comparison between the results of Marsden & Steel (1994), denoted MS, and this paper. Note that orbital elements have been taken from Marsden & Steel. The impact probabilities are quoted in units of 10^-8 per revolution

In order to test the performance of the algorithm with a large ensemble, we examined the set of 682 asteroids with diameters D>50km used by Farinella & Davis (1992) and later by Bottke et al. (1994) and Vedder (1998). The distribution of collision velocities was determined for every interacting pair and the total summed distribution is shown in Fig. 4. The mean colision velocity is 5.30 km s^-1, which may be compared with the values calculated by Farinella & Davis (1992); Bottke et al. (1994) and Vedder (1998) of $5.81\,$km s^-1, $5.29\,$km s^-1 and $4.22\,$km s^-1 respectively. Similarly, the intrinsic collision probability for this sample (assuming a diameter of 1km for each object, i.e. corresponding to an interaction cross-section of $\pi$km²; cf. Table 1), is $2.79\ 10^{-18}$yr^-1 km^-2, which may be compared with the values $2.85\ 10^{-18}$yr^-1 km^-2 and $3.27\ 10^{-18}$yr^-1 km^-2 reported by Farinella & Davis (1992) and Vedder (1998) respectively. The method of the latter author appears to lead to a slightly lower mean impact velocity and a slightly higher mean intrinsic collision probability. Use of the present algorithm resulted in a total collision probability for the 682-asteroid ensemble of $7.26\ 10^{-9}\,$yr^-1, implying a mean time $\sim$140Myr for collisions between objects in the ensemble. Collisions between these large objects could result in the formation of asteroid families, and possibly showers of kilometre-sized fragments on Earth-crossing orbits via fast-track resonant dynamical pathways (Zappalà et al. 1998).

  

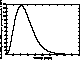Figure 4: The figure shows the frequency distribution of collision velocities for main-belt asteroids with diameters d > 50 km