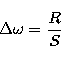Up: An algorithm for determining
Subsections
The algorithm is designed to work with two arbitrary elliptical orbits.
Due to its nature some classes of problem (i.e. objects in secular,
mean-motion and Kozai resonances, including extreme cases of
(e, 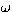 )-coupling) may be inappropriate for this approach. The
basic assumptions involved are:
)-coupling) may be inappropriate for this approach. The
basic assumptions involved are:
- 1.
- each orbit has fixed semi-major-axis (a), eccentricity (e)
and inclination (i);
- 2.
- the rate of variation of the argument of perihelion (
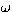 )is greater than that of any of the other elements;
)is greater than that of any of the other elements;
- 3.
- the variations of the respective arguments of perihelia are not
correlated.
In addition, we assume that the objects are of small size compared to
their orbits, and that there is no significant gravitational focusing.
The algorithm is readily extended to incorporate the latter, as we show
in Sect. 3.
Let us suppose that each orbit has semi-major axis, eccentricity and
inclination (a1, e1, i1) and (a2, e2, i2) respectively. The
longitudes of the ascending nodes (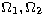 respectively) are
assumed to be fixed, as are the inclinations, and hence so too is the
mutual inclination
respectively) are
assumed to be fixed, as are the inclinations, and hence so too is the
mutual inclination 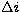 of the two orbital planes. We allow the
arguments of perihelion of each object,
of the two orbital planes. We allow the
arguments of perihelion of each object, 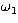 and
and 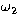 , to
take all possible values in the range (
, to
take all possible values in the range (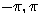 ). This defines a
two-dimensional phase space in which the differential collision
probability at each point,
). This defines a
two-dimensional phase space in which the differential collision
probability at each point, 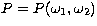 , can be evaluated.
The total collision probability is then
, can be evaluated.
The total collision probability is then
| 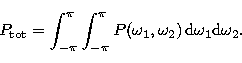 |
(1) |
Over most of this phase space the collision probability
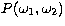 is zero because interactions can only occur when
the mutual nodes are sufficiently close. Without loss of generality the
coordinate system can be chosen so that the origin lies at the focus of
the two orbits, the (x,y)-plane coincides with the orbital plane of the
first orbit, and the x-axis lies along the line of intersection of the
two orbital planes (Fig. 1). In each case
is zero because interactions can only occur when
the mutual nodes are sufficiently close. Without loss of generality the
coordinate system can be chosen so that the origin lies at the focus of
the two orbits, the (x,y)-plane coincides with the orbital plane of the
first orbit, and the x-axis lies along the line of intersection of the
two orbital planes (Fig. 1). In each case 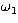 and
and 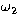 are measured in the orbital plane from the mutual node.
are measured in the orbital plane from the mutual node.
![\begin{figure}
\includegraphics[width=8.5cm]{ds7564f1.eps}\end{figure}](/articles/aas/full/1998/21/ds7564/Timg10.gif) |
Figure 1:
Intersection of orbital planes, illustrating the mutual
inclination, 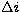 , and the definition of the argument of
perihelion, , and the definition of the argument of
perihelion, 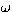 , of one orbit measured with respect to the mutual
line of nodes , of one orbit measured with respect to the mutual
line of nodes |
In general, the heliocentric distances r of the ascending or descending
nodes are given by
| 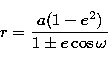 |
(2) |
and collisions may occur at the ascending node when
|  |
(3) |
with a similar expression
| 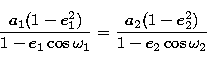 |
(4) |
for collisions at the descending node. Choosing the ascending node and
replacing a(1-e2) with p, and solving for 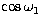 we obtain:
we obtain:
| 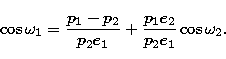 |
(5) |
This relation takes the general form
| 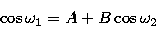 |
(6) |
where
| 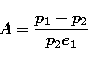 |
(7) |
and
| 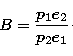 |
(8) |
This can be differentiated to give
| 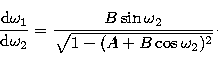 |
(9) |
Relations (6) through (8) and corresponding equations for
the descending node define the locus of the points in
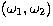 -space where collisions may occur, illustrated
in Figure 2. Equation (9) is used to determine the tangent and
normal to this curve. We note that the curve is symmetrical on both axes,
so that looking at one point of intersection there are at most three
others with conjugate configurations.
-space where collisions may occur, illustrated
in Figure 2. Equation (9) is used to determine the tangent and
normal to this curve. We note that the curve is symmetrical on both axes,
so that looking at one point of intersection there are at most three
others with conjugate configurations.
![\begin{figure}
\includegraphics[angle=-90,width=8.5cm]{ds7564f2.eps}\end{figure}](/articles/aas/full/1998/21/ds7564/Timg22.gif) |
Figure 2:
The figure illustrates the symmetry of the solutions of
Eq. (6) in (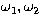 )-space for two typical pairs of
orbits. Each pair of orbits has two solutions. The first pair has
solutions denoted "1" and "2"; the second has solutions denoted "3" and
"4". In each case these correspond to an intersection at the ascending or
descending node. The important points to note are that (i) each solution
shows four-fold symmetry, and one can be obtained from the other; and
(ii) )-space for two typical pairs of
orbits. Each pair of orbits has two solutions. The first pair has
solutions denoted "1" and "2"; the second has solutions denoted "3" and
"4". In each case these correspond to an intersection at the ascending or
descending node. The important points to note are that (i) each solution
shows four-fold symmetry, and one can be obtained from the other; and
(ii) 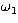 is always a monotonically increasing or decreasing
function of is always a monotonically increasing or decreasing
function of 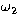 in the principal quadrant, depending on whether
the intersection occurs at the the ascending or descending node
respectively in the principal quadrant, depending on whether
the intersection occurs at the the ascending or descending node
respectively |
We emphasize that, due to the finite size of real objects, collisions
may occur not only on this curve but also in its immediate vicinity,
over a range 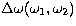 measured in the
measured in the
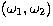 -plane perpendicular to the curve of
intersection. For spherical particles
-plane perpendicular to the curve of
intersection. For spherical particles 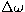 is proportional
to the combined radius of interaction R=R1+R2 of the two
bodies. Moreover, moving perpendicular to the curve of intersection,
it is straightforward to show that the differential collision
probability at a distance
is proportional
to the combined radius of interaction R=R1+R2 of the two
bodies. Moreover, moving perpendicular to the curve of intersection,
it is straightforward to show that the differential collision
probability at a distance 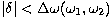 from the collision point
from the collision point 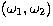 is
is
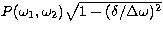 , so the
differential collision probability integrated normal to the curve of
intersection is
, so the
differential collision probability integrated normal to the curve of
intersection is
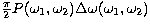 .
.
The total collision probability is then calculated by integrating
along the curves of intersection, choosing small line elements of each
curve, determining their dimensions and summing their resulting
contributions to the total probability. The direction along each curve
of intersection is chosen using 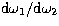 from
Eq. (9). The stepping can be mirrored to allow for the
symmetry, but differing geometry (associated with the particles'
relative velocities at collision) means that P and
from
Eq. (9). The stepping can be mirrored to allow for the
symmetry, but differing geometry (associated with the particles'
relative velocities at collision) means that P and 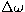 may be different for different mirrored points.
may be different for different mirrored points.
Determination of 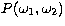 and
and 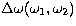 requires a model of the encounter
geometry. We adopt a simple vector approach in which each body is
assumed to move at a constant velocity, denoted
requires a model of the encounter
geometry. We adopt a simple vector approach in which each body is
assumed to move at a constant velocity, denoted 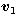 and
and 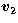 respectively, during the close encounter. The respective vectors
(see Fig. 3) are determined using the classical formulae for
heliocentric elliptical motion (Roy 1988):
respectively, during the close encounter. The respective vectors
(see Fig. 3) are determined using the classical formulae for
heliocentric elliptical motion (Roy 1988):
| 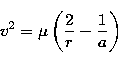 |
(10) |
where 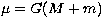 and G is the gravitational constant, M is the mass
of the central body and m is the mass of the orbiting particle. If we
choose
and G is the gravitational constant, M is the mass
of the central body and m is the mass of the orbiting particle. If we
choose 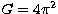 , M=1 and m=0 we have:
, M=1 and m=0 we have:
| 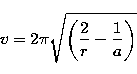 |
(11) |
and for the angle 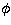 between the velocity and radius vectors at the
node
between the velocity and radius vectors at the
node
| 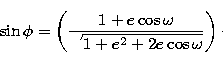 |
(12) |
(Note that 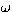 is measured from the mutual node, and that for
simplicity we have dropped subscripts 1 and 2 from
Eqs. (10)-(12).)
For the first orbit, which lies in the (x,y)-plane, the velocity vector
is (Fig. 3):
is measured from the mutual node, and that for
simplicity we have dropped subscripts 1 and 2 from
Eqs. (10)-(12).)
For the first orbit, which lies in the (x,y)-plane, the velocity vector
is (Fig. 3):
| 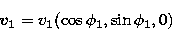 |
(13) |
and for the second, whose plane is inclined at an angle 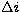 to the
first, we have
to the
first, we have
|  |
(14) |
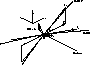 |
Figure 3:
Diagram to illustrate the simplified vector encounter geometry
described in the text |
In order for a collision to take place, both particles must arrive at
the point of intersection of their respective orbits at the same
moment, within a small time interval 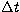 . We use
. We use 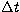 to
calculate the collision probability
to
calculate the collision probability  at the
point
at the
point 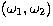 on the curve of intersection, and then use
the vectors
on the curve of intersection, and then use
the vectors 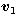 and
and 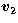 to evaluate the range
to evaluate the range 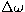 associated with this point on the curve.
associated with this point on the curve.
Moving the origin of the coordinate system to the point at which the
two paths cross, the motion of the two particles near the mutual node
or collision point can be described by
| 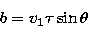 |
(15) |
where 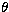 is the angle between the two position vectors
is the angle between the two position vectors 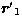 and
and 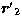 in the new frame. By replacing the maximum value of
impact parameter b which produces a collision, namely b=R where R
is the radius of interaction for both particles (i.e. R = R1
+ R2 for spheres of radius R1 and R2 respectively), we
calculate the maximum value of
in the new frame. By replacing the maximum value of
impact parameter b which produces a collision, namely b=R where R
is the radius of interaction for both particles (i.e. R = R1
+ R2 for spheres of radius R1 and R2 respectively), we
calculate the maximum value of 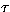 , and hence obtain
, and hence obtain 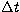 using
using
| 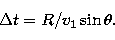 |
(16) |
Since the temporal window for a collision is 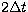 per
revolution, the differential collision probability per unit time for
such intersecting orbits is
per
revolution, the differential collision probability per unit time for
such intersecting orbits is 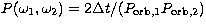 , where
, where
 and
and 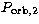 denote the orbital periods of each particle.
denote the orbital periods of each particle.
We now determine the magnitude of the range 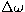 perpendicular to the curve of intersection. We define
perpendicular to the curve of intersection. We define 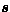 to be
the vector that describes the relative motion of the two encounter
vectors as
to be
the vector that describes the relative motion of the two encounter
vectors as 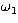 and
and 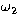 are varied normal to the curve of
intersection, and introduce a separation parameter S, analogous to
the impact parameter b, whose value equals R at the extremum
are varied normal to the curve of
intersection, and introduce a separation parameter S, analogous to
the impact parameter b, whose value equals R at the extremum
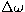 . We thus have
. We thus have
| 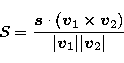 |
(17) |
where
| 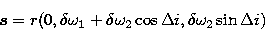 |
(18) |
and 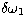 and
and 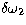 denote the respective
variations of
denote the respective
variations of 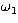 and
and 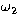 perpendicular to the curve of
intersection, with
perpendicular to the curve of
intersection, with 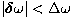 . Here, r
is the distance from the Sun where the interaction occurs.
. Here, r
is the distance from the Sun where the interaction occurs.
Therefore 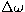 is simply calculated from
is simply calculated from
| 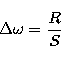 |
(19) |
and the total collision probability is evaluated by summing the values
of 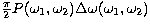 along the curve of intersection in the
along the curve of intersection in the 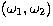 -plane for a
statistically sufficient number of points.
-plane for a
statistically sufficient number of points.


Up: An algorithm for determining
Copyright The European Southern Observatory (ESO)
![]() )-coupling) may be inappropriate for this approach. The
basic assumptions involved are:
)-coupling) may be inappropriate for this approach. The
basic assumptions involved are:
![]() respectively) are
assumed to be fixed, as are the inclinations, and hence so too is the
mutual inclination
respectively) are
assumed to be fixed, as are the inclinations, and hence so too is the
mutual inclination ![]() of the two orbital planes. We allow the
arguments of perihelion of each object,
of the two orbital planes. We allow the
arguments of perihelion of each object, ![]() and
and ![]() , to
take all possible values in the range (
, to
take all possible values in the range (![]() ). This defines a
two-dimensional phase space in which the differential collision
probability at each point,
). This defines a
two-dimensional phase space in which the differential collision
probability at each point, ![]() , can be evaluated.
The total collision probability is then
, can be evaluated.
The total collision probability is then
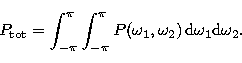
![\begin{figure}
\includegraphics[width=8.5cm]{ds7564f1.eps}\end{figure}](/articles/aas/full/1998/21/ds7564/Timg10.gif)
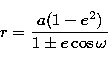

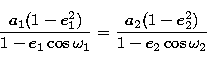
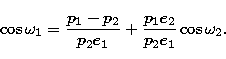
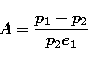
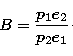
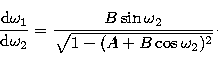
![]() measured in the
measured in the
![]() -plane perpendicular to the curve of
intersection. For spherical particles
-plane perpendicular to the curve of
intersection. For spherical particles ![]() is proportional
to the combined radius of interaction R=R1+R2 of the two
bodies. Moreover, moving perpendicular to the curve of intersection,
it is straightforward to show that the differential collision
probability at a distance
is proportional
to the combined radius of interaction R=R1+R2 of the two
bodies. Moreover, moving perpendicular to the curve of intersection,
it is straightforward to show that the differential collision
probability at a distance ![]() from the collision point
from the collision point ![]() is
is
![]() , so the
differential collision probability integrated normal to the curve of
intersection is
, so the
differential collision probability integrated normal to the curve of
intersection is
![]() .
.![]() from
Eq. (9). The stepping can be mirrored to allow for the
symmetry, but differing geometry (associated with the particles'
relative velocities at collision) means that P and
from
Eq. (9). The stepping can be mirrored to allow for the
symmetry, but differing geometry (associated with the particles'
relative velocities at collision) means that P and ![]() may be different for different mirrored points.
may be different for different mirrored points.
![]() and
and ![]() requires a model of the encounter
geometry. We adopt a simple vector approach in which each body is
assumed to move at a constant velocity, denoted
requires a model of the encounter
geometry. We adopt a simple vector approach in which each body is
assumed to move at a constant velocity, denoted ![]() and
and ![]() respectively, during the close encounter. The respective vectors
(see Fig. 3) are determined using the classical formulae for
heliocentric elliptical motion (Roy 1988):
respectively, during the close encounter. The respective vectors
(see Fig. 3) are determined using the classical formulae for
heliocentric elliptical motion (Roy 1988):
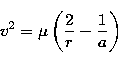
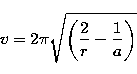
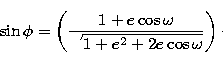
![]() perpendicular to the curve of intersection. We define
perpendicular to the curve of intersection. We define ![]() to be
the vector that describes the relative motion of the two encounter
vectors as
to be
the vector that describes the relative motion of the two encounter
vectors as ![]() and
and ![]() are varied normal to the curve of
intersection, and introduce a separation parameter S, analogous to
the impact parameter b, whose value equals R at the extremum
are varied normal to the curve of
intersection, and introduce a separation parameter S, analogous to
the impact parameter b, whose value equals R at the extremum
![]() . We thus have
. We thus have
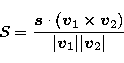
![]() is simply calculated from
is simply calculated from