 |
We have started our comparison project by selecting several representative polytropic models, the parameters of which are shown in Tables 1-2. We have chosen
Note that, the maximum mass model almost coincides with the maximum angular velocity model, unless there is a large phase transition at densities close to the central density of the maximum mass star (cf. Cook et al. 1994b and Stergioulas & Friedman 1995). For all EOSs in this comparison the two models almost coincide.
In order to evaluate the performance of our numerical codes for models with discontinuous density distribution, we also compare a number of homogeneous models which cover both highly relativistic and Newtonian, rapidly rotating and nonrotating cases, as shown in Tables 3 and 4 (the contents of these tables will be described in Sect. 5.4).
As discussed in the previous section, we use six representative
realistic EOSs: C, G, L, WFF3+FPS, WFF3+NV and FPS. In addition, we use
the causal limit EOS CLES. For each equation of state, we compute
several models as shown Tables 5 - 7.
The models correspond to
the maximum mass model, a fast rotating ![]() model and a
nonrotating model for each EOS.
model and a
nonrotating model for each EOS.
For this comparison project, KEH(OR) and KEH(SF) have used grids with
(![]() and (
and (![]() ) (angular
) (angular![]() radial)
grid-points. In the equatorial plane, half of the radial grid-points
are inside the star. BGSM uses 21
radial)
grid-points. In the equatorial plane, half of the radial grid-points
are inside the star. BGSM uses 21 ![]() 41 or 33
41 or 33 ![]() 65 grid
points (note that the notion of "grid points'' is not very significant
for a spectral method; the above numbers should better be referred to as
the numbers of basis functions employed in the expansions of the
physical fields).
65 grid
points (note that the notion of "grid points'' is not very significant
for a spectral method; the above numbers should better be referred to as
the numbers of basis functions employed in the expansions of the
physical fields).
Here we summarize the notation of computed physical quantities:
![]() Central energy density
Central energy density
![]() Ratio of polar to equatorial radii
Ratio of polar to equatorial radii
![]() Angular velocity of the star
Angular velocity of the star
M0 Baryon mass
![]() Proper mass
Proper mass
M Gravitational mass
![]() Equatorial circumferential radius
Equatorial circumferential radius
![]() Equatorial coordinate radius
Equatorial coordinate radius
J Total angular momentum
I Moment of inertia about the rotation axis
T Rotational energy
W Gravitational energy
![]() Velocity of comoving observer at the equator
Velocity of comoving observer at the equator
relative to the locally non-rotating observer
![]() Polar redshift
Polar redshift
![]() Central redshift
Central redshift
![]() Equatorial redshift in the backward direction
Equatorial redshift in the backward direction
![]() Equatorial redshift in the forward direction
Equatorial redshift in the forward direction
e Intrinsic eccentricity of the star's surface
GRV2 Two dimensional virial identity
GRV3 Three dimensional virial identity.
Some of the quantities in the above list can be expressed as follows:
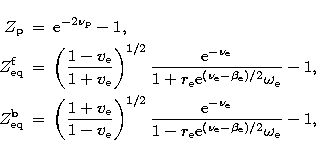 |
(26) | |
| (27) | ||
| (28) |
 |
(29) |
 |
(30) |
![\begin{eqnarray}
M &=& 2 \pi \int \Biggl[ {\rm e}^{2 \alpha + \beta}
\left\{ {(...
...p) v \over
1-v^2} \Biggr] r^2 \sin \theta {\rm d}r {\rm d}\theta,\end{eqnarray}](/articles/aas/full/1998/18/ds7680/img102.gif) |
||
| (31) |
 |
(32) |
 |
(33) |
| (34) |
 |
(35) |
| (36) |
![\begin{displaymath}
{\rm d} \sigma^2 = {\rm e} ^{2 \beta} r^2 \sin^2 \theta {\rm...
...heta}
\right)^2 + r_{\rm s}(\theta)^2 \right] {\rm d} \theta^2.\end{displaymath}](/articles/aas/full/1998/18/ds7680/img108.gif) |
(37) |
| (38) |
![\begin{displaymath}
{\rm d} \sigma^2 = \left[ \left({ {\rm d} R_{\rm s} \over {\...
...ight)^2 + 1 \right] {\rm d}z^2 + R_{\rm s}^2 {\rm d} \varphi^2.\end{displaymath}](/articles/aas/full/1998/18/ds7680/img111.gif) |
(39) |
| (40) |
 |
||
| (41) |
 |
(42) |
 |
(43) | |
| (44) | ||
| (45) | ||
| (46) | ||
| (47) | ||
| (48) | ||
| (49) | ||
| (50) | ||
| (51) | ||
| (52) |
Equilibrium configurations in Newtonian gravity satisfy the following relation:
| (53) |
In general relativity, similar relations were first found by Bonazzola (1973).
Recently, two virial identities in general relativity have been discovered
by Gourgoulhon & Bonazzola (1994) and Bonazzola & Gourgoulhon (1994).
Those identities are valid for a general asymptotically flat spacetime.
We can use these identities to estimate the numerical error.
Let us define two quantities ![]() and
and ![]() as follows:
as follows:
![\begin{displaymath}
\lambda_2 \equiv \frac{ \displaystyle 8 \pi \int_0^{+\infty}...
...\partial \omega
\right] \, r \, {\rm d}r \, {\rm d}\theta }, \end{displaymath}](/articles/aas/full/1998/18/ds7680/img120.gif) |
(54) |
![\begin{eqnarray}
\lambda_3 &\equiv&
4 \pi \int_0^{+\infty} \int_0^{\pi} \left[...
...g] {\rm e}^{\psi} \, r \, {\rm d}r\, {\rm d}\theta \Bigg\}
^{-1},\end{eqnarray}](/articles/aas/full/1998/18/ds7680/img121.gif) |
||
| (55) |
 |
(56) |
 |
(57) | |
| (58) |
 |
(59) | |
| (60) |
In practice, however, it should be noted that the virial identities
in the above form are not always close to the accuracy of
numerical results. In particular, for GRV2 the integration is
done by integrating in the ![]() coordinate as seen from the
definition of GRV2. If one does not use the
coordinate as seen from the
definition of GRV2. If one does not use the ![]() coordinate
for solving equilibrium structures, one needs to change variables
and in that procedure accuracy may be lost and the resultant
values may become worse than the "real" accuracy before the variable change.
coordinate
for solving equilibrium structures, one needs to change variables
and in that procedure accuracy may be lost and the resultant
values may become worse than the "real" accuracy before the variable change.
Concerning the quantity GRV3, the metric potentials in the vacuum region contribute to the integral considerably. It implies that if only the finite regions are treated, as in the KEH(OR) code, a large portion of the integrand cannot be taken into account, However, the expressions for the GRV2 and GRV3 are not unique because we can do the integral by part and replace the second derivatives with the matter terms, using Einstein's equations. In this way, the contribution far away from the star becomes less important. In the KEH(OR) code, GRV2 and GRV3 are evaluated through
 |
||
| (61) |
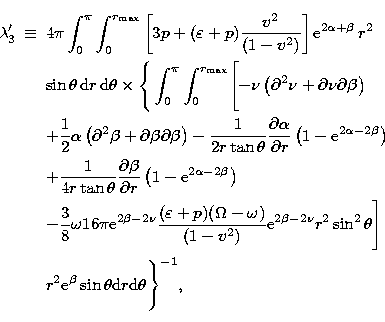 |
||
| (62) |
 |
(63) |
This rewrite does not break the mathematical identity. In a sense, it may make "identity" more trivial, and then what information the identities provide us becomes unclear. However, as far as the same expression of the identity in the same code is used, they can play a role as indicators of accuracy among models solved by each code.
Tables 1 and 2 display results for polytropes with
index ![]() and 1.5. For each value of the polytropic index N we compute the
following models:
and 1.5. For each value of the polytropic index N we compute the
following models:
For the constant density case (N = 0), the spherical Newtonian and
spherical relativistic models are displayed in Table 3
and the rapidly
rotating Newtonian and rapidly rotating relativistic models in
Table 4.
While all other models are specified by the central energy density
![]() and the ratio of the polar radius to the equatorial
radius
and the ratio of the polar radius to the equatorial
radius ![]() , constant density models are specified by their
central pressure and
, constant density models are specified by their
central pressure and ![]() .
.
For realistic equations of state, spherical models are shown in
Table 5
and rotating models with ![]() (br: binary
pulsar mass and relativistic) and maximum mass models are shown in
Tables 6 and 7.
For the equation of state L, model L(L)mr uses four-point
Lagrange interpolation, while L(H)mr is the same model but computed
using cubic Hermite interpolation.
(br: binary
pulsar mass and relativistic) and maximum mass models are shown in
Tables 6 and 7.
For the equation of state L, model L(L)mr uses four-point
Lagrange interpolation, while L(H)mr is the same model but computed
using cubic Hermite interpolation.
From the tables displaying polytropic models
one can see that the three codes have a good
agreement on most quantities especially for soft polytropes.
For stiff polytropes (N<1.0) the agreement is somewhat smaller.
For constant density models, the relative differences between the three
codes become several percent.
More sensitive quantities are the three redshifts and the eccentricity.
It should be noted that redshift factors are local quantities which reflect the
metric potentials at each point. This implies that local values of the
metric potentials do not have the same agreement between different
numerical codes, as integrated global quantities. For the
eccentricity, one needs to compute the length along the surface of the
star (see the definition of the eccentricity (42)). Since in the
KEH codes ![]() is used as the angular variable there arise
numerical errors near the pole region, i.e.
is used as the angular variable there arise
numerical errors near the pole region, i.e. ![]() . Thus, the
differences in the values of the eccentricity also reflect this numerical
error due to the choice of coordinates. This causes differences of up to a
few percent in the eccentricity for rapidly rotating models.
On the other hand, global quantities such as angular velocity, mass, radius and
angular momentum agree quite well among results of different codes.
. Thus, the
differences in the values of the eccentricity also reflect this numerical
error due to the choice of coordinates. This causes differences of up to a
few percent in the eccentricity for rapidly rotating models.
On the other hand, global quantities such as angular velocity, mass, radius and
angular momentum agree quite well among results of different codes.
From Tables 5-7, similar tendencies can be observed for realistic equations of state. Models for the most EOSs, except EOS CLES, have a good agreement between the three codes, although the agreement is not as good as for polytropic models. By comparing models constructed with EOSs WFF(FPS) and WFF(NV), it is evident that the choice of the low density EOSs affects very little the structure of the star.
The main reason for the large differences in the constant density case is that the discontinuous density distribution is creating Gibbs phenomena near the surface and this affects all three codes. The reason for the smaller agreement for realistic EOSs, compared to polytropic EOSs, is that the necessary interpolation between tabulated data affects the accuracy with which the equation of hydrostationary equilibrium is satisfied. For EOS L, the choice of the interpolation scheme also affects the accuracy of the computed models, with the cubic Hermite scheme being a better choice compared to a four-point Lagrange interpolation (see the discussion in a later section). For the other realistic EOSs the choice of the interpolation scheme had a negligible effect on the accuracy of computed models.
In order to investigate further the differences among numerical results obtained by the three codes, we show more detailed results for models: N15sn, N15mr and N05sn in Table 8, N05mr in Table 9, N00sn, N00rn and N00sr in Table 10, N00rr in Table 11, Gmr, Lsr and L(L)mr in Table 12, L(H)mr, WFF(FPS)sr and WFF(FPS)br in Table 13 and CLESmr in Table 14. In these tables, values to eight figures for each physical quantity are shown, as well as the relative differences among results of the three codes.
The three relative differences ![]() ,
, ![]() and
and ![]() are defined as
are defined as
 |
(64) | |
| (65) | ||
| (66) |
From the same tables, we see that the agreement between the KEH(OR) and BGSM codes is similar to the agreement between KEH(SF) and BGSM in the global quantities of model N15mr but to within 10-3 for the local quantities of this model. For the stiffer polytrope N05mr the agreement is 10-3 and 10-2 for global and local quantities, respectively. This difference in accuracy between KEH(SF) and KEH(OR) is expected, since in KEH(OR) boundary conditions are applied only approximately at a finite distance from the star. Considering how close to the star the domain of integration is truncated, the KEH(OR) code performs very well. This is explained as follows:
Since the integration is performed over only a finite region, the truncated
part of the integral, ![]() , can be expressed as
, can be expressed as
 |
(67) |
 |
(68) |
 |
||
| (69) |
In the extreme case of constant density models (Tables 10 and 11), the three codes agree on the computed physical quantities typically only within a few percent and this is caused by the sharp density discontinuity at the surface of the star. The numerical schemes in this comparison assume that the density distribution is a smooth function of coordinates, thus, in the case of density discontinuities, this assumption is violated and Gibbs phenomena appear, resulting in low accuracy of the computed models.
From Tables 12-14 it follows that the agreement of the KEH(SF) code to the BGSM code is between 10-3 and 10-4 for realistic EOSs, except for EOS CLES, where the agreement is an order of magnitude smaller. KEH(OR) and BGSM agree on the realistic models within 10-2 and 10-3, i.e. similar to the agreement for the N=0.5 polytrope. The somewhat lesser agreement for realistic EOSs is due to the use of interpolation between the tabulated equation of state data (see the discussion next).
In Tables 8 to 14,
we also display the virial quantities GRV2 and GRV3. In the ideal case,
these should exactly vanish, so the smaller the values for GRV2 and GRV3 are, the
better is the accuracy of the computed model. The opposite is not always true,
i.e. in some models the computed values for GRV2 or GRV3 do not reflect an overall
better agreement in physical quantities among the different codes. This indicates that
the computation of GRV2 and GRV3 may itself be prone to numerical error. This seems
to be the case for GRV2 in rapidly rotating models computed with the KEH(SF) code, where
one first has to interpolate data between ![]() and
and ![]() grids to be
able to compute GRV2. Note that the displayed values of the two virial quantities
for the KEH(OR) code correspond to the modified virial identities
(61) and (62) and not to the original identities.
The computation of GRV3 for the KEH(OR) code is affected significantly by the
truncation of the domain of integration.
grids to be
able to compute GRV2. Note that the displayed values of the two virial quantities
for the KEH(OR) code correspond to the modified virial identities
(61) and (62) and not to the original identities.
The computation of GRV3 for the KEH(OR) code is affected significantly by the
truncation of the domain of integration.
Copyright The European Southern Observatory (ESO)