As redshift factors differ by about 10% for the constant density, relativistic
model N00rr between the three codes (while the agreement global quantities
is within a few %) we compare directly the local values of metric potentials for
several models. Figures 1 to 16 show the four metric potentials (upper panel)
and the relative differences in them between BGSM and KEH(OR) (middle panel)
and KEH(SF) and BGSM (lower panel) for the models N05mr, N15mr, L(L)mr
and WFF(FPS)br. The metric potentials are graphed against the coordinate r
in the equatorial plane (![]() , solid line) and along the axis of rotation
(
, solid line) and along the axis of rotation
(![]() , dashed line). The range of the coordinate r is the twice the equatorial
radius of the star.
, dashed line). The range of the coordinate r is the twice the equatorial
radius of the star.
In general, the agreement in the local values of the metric potentials reflects the
agreement in the computed physical parameters of models. In these graphs, several
significant behaviors can be pointed out: First, there
are high frequency and small amplitude oscillations at the inner
part of the stars for all models. Second, the differences between the
results of KEH(OR) and those of the other two codes are growing outside the stars
as r increases. Third, although the differences between the KEH(SF) and BGSM codes
are very small for models N05mr, N15mr and WFF(FPS)br, there appear larger
differences for the stiff model L(L)mr. Fourth, there appears a larger amplitude
oscillation in the metric potential ![]() on the axis of rotation, close to the
surface.
on the axis of rotation, close to the
surface.
The first behavior is due to the integration scheme of the KEH code, i.e. the Simpson scheme. In general, the Simpson scheme gives results with higher precision, compared with those obtained by the trapezoidal scheme. However, in the KEH scheme, the integrands contain nonsmooth functions with respect to the radial coordinate, because of the nature of the Green's functions. The non-uniform distribution of the weight factor in Simpson's scheme for nonsmooth functions results in oscillating behaviors with very small amplitudes, which cannot be noticed in the behavior the integrated quantities.
The second behavior in the original KEH code is caused by the "truncation" of the domain of integration at a finite distance from the star, instead of integrating over the whole space.
The large differences in the metric potentials between KEH(SF) and BGSM for EOS L, could be accounted to the stiffness of the equation of state, but the differences between KEH(OR) and BGSM for the same model are not as large, and we have not an explanation for that.
The oscillations in ![]() on the axis of rotation near the surface are present
also for the soft N=1.5 polytropes, while for N=0.5 they are larger. This
indicates that terms in the field equations for
on the axis of rotation near the surface are present
also for the soft N=1.5 polytropes, while for N=0.5 they are larger. This
indicates that terms in the field equations for ![]() are very sensitive to
the presence of the surface and the accompanying Gibbs phenomenon. Even
for N=1.5 polytropes, where the density goes to zero smoothly at the surface,
there is a small scale Gibbs phenomenon, due to the finite number of grid
points used to represent the region of integration.
are very sensitive to
the presence of the surface and the accompanying Gibbs phenomenon. Even
for N=1.5 polytropes, where the density goes to zero smoothly at the surface,
there is a small scale Gibbs phenomenon, due to the finite number of grid
points used to represent the region of integration.
An important factor for the
local accuracy of models constructed with realistic equations of state
is the method of interpolation of the energy vs. pressure data given in
an EOS table. While global quantities are not affected significantly,
the virial identities for realistic EOSs, are sensitive to the interpolation scheme
This can be considered to reflect the nature of the interpolation
scheme as mentioned before. If we define the enthalpy (H) by
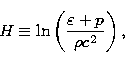 |
(70) |
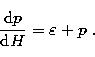 |
(71) |
The four point Lagrange interpolation does not satisfy the Gibbs-Duhem
relation because it only reproduces the values of the discrete points,
but there is no guarantee for the reproduction of the derivatives.
This explains why the GRV2 and GRV3 errors are bad, even in the
nonrotating case (GRV2 = 3E-03, GRV3 = 1E-02 for model Lsr)
as compared to ![]() for polytropic models (see e.g.
Bonazzola et al. 1993). The GRV2 and GRV3 error
indicators thus do not reflect the precision of the code but the bad
thermodynamical behavior of the tabulated EOS.
for polytropic models (see e.g.
Bonazzola et al. 1993). The GRV2 and GRV3 error
indicators thus do not reflect the precision of the code but the bad
thermodynamical behavior of the tabulated EOS.
The advantage of the cubic Hermite interpolation is that the Gibbs-Duhem relation is automatically satisfied because this interpolation reproduces not only the values themselves but also the derivatives (Swesty 1996). Moreover, in our case, the energy density and the baryon number density are obtained by
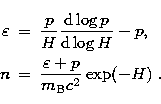 |
(72) | |
| (73) |
The comparison of three different codes for constructing rapidly rotating relativistic neutron star models demonstrates that the BGSM and KEH schemes used are highly accurate for typical polytropic models - when the field equations are solved to infinity - and for models constructed with realistic equations of state, that do not have phase transitions. If one approximates neutron stars as constant density stars, then Gibbs phenomena at the discontinuous surface reduce the accuracy of the computed models. If high accuracy in such models and in models with phase transitions is desired, then modified numerical schemes - free of Gibbs phenomena - need to be used. Such numerical schemes could employ, for example, surface fitted coordinates. Such a scheme has been presented recently by Bonazzola et al. (1998a) in the framework of spectral methods and looks promising for rotating stellar models. Further, we demonstrated that the metric potentials are subject to various local oscillatory behaviors, even if integrated quantities have very good accuracy. This observation is important for the effort of constructing initial data for the numerical evolution of rotating relativistic neutron star models.
Acknowledgements
We would like to thank S. Bonazzola and J.L. Friedman for very helpful discussions. This research has been supported in part by NSF grant PHY-9507740 and by the Grant-in-Aid for Scientific Research of the Japanese Ministry of Education, Science and Culture. N.S. wishes to acknowledge the generous hospitality of the Max Planck Institute for Gravitational Physics, Potsdam, where part of this paper was completed.
Copyright The European Southern Observatory (ESO)