

Up: Construction of highly accurate
Subsections
We use the following relation as a polytropic equation of state
(Tooper 1965):
| 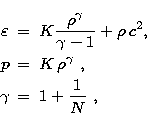 |
(23) |
| (24) |
| (25) |
where K and N are the polytropic constant and polytropic index, respectively, while
 is the rest mass density.
is the rest mass density.
It should be noted that this equation of state includes the limiting
case of 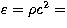 constant, when
constant, when 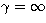 (N=0). The constant density models are also called homogeneous models.
For polytropes of index N<1.0, the density does not go to zero smoothly
at the surface and the first derivatives of the density across the surface are discontinuous.
This kind of discontinuity may become the cause of unfavorable behavior
of solutions, unless it is treated carefully. For constant density models, the
situation is even worse, since the density itself is discontinuous across the surface.
(N=0). The constant density models are also called homogeneous models.
For polytropes of index N<1.0, the density does not go to zero smoothly
at the surface and the first derivatives of the density across the surface are discontinuous.
This kind of discontinuity may become the cause of unfavorable behavior
of solutions, unless it is treated carefully. For constant density models, the
situation is even worse, since the density itself is discontinuous across the surface.
Although polytropic EOSs are not as realistic as tabulated EOSs (but one can
reproduce neutron star bulk properties with an 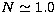 polytrope),
they are helpful to check numerical codes. Since the
hydrostationary equation can be analytically integrated and no
additional numerical errors arise in solving it.
polytrope),
they are helpful to check numerical codes. Since the
hydrostationary equation can be analytically integrated and no
additional numerical errors arise in solving it.
As discussed in the introduction, the main uncertainties about
neutron star properties are related to the unknown interactions of the neutron star
matter at high density regions. In the last decades, many equations of state
have been proposed by considering different kinds of interactions into account.
A large collection of representative equations of state were compiled by Arnett &
Bowers (1977), who constructed nonrotating neutron star models and
obtained physical quantities for slowly rotating neutron stars.
We will choose three equations of state of Arnett & Bowers' compilation,
i.e. equations C, G and L according to their notation. Equations C, G
and L are those derived by Bethe & Johnson (1974), Canuto & Chitre (1974)
and Pandharipande & Smith (1975) (see also Pandharipande et al.
1976), respectively.
Those equations of state were also used by Friedman et al. (1986) for
constructing rapidly rotating relativistic neutron stars models.
In addition to these equations of state we also employ the WFF3
(UV14+TNI) equation of state by Wiringa et al. (1988), the FPS
equation of state by Lorenz et al. (1993), and the equation of state
which represents a causal limit (CLES).
Some characteristic features of each equation of state can be summarized
as follows.
EOS C is of intermediate stiffness.
The maximum gravitational mass of a spherical neutron star for this
EOS is 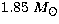 . The density range is from
. The density range is from 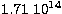 g cm-3 to
g cm-3 to 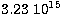 g cm-3. Hyperons as
well as nucleons are taken into account. The interaction is assumed
non-relativistic and represented by the modified Reid soft core
potential with non-integer parameters. To include the many-body
theory, the constrained variational principle is employed. This
equation of state is joined to the composite BBP(
g cm-3. Hyperons as
well as nucleons are taken into account. The interaction is assumed
non-relativistic and represented by the modified Reid soft core
potential with non-integer parameters. To include the many-body
theory, the constrained variational principle is employed. This
equation of state is joined to the composite BBP(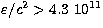 g cm-3) - BPS (104 g cm
g cm-3) - BPS (104 g cm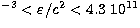 g cm-3) - FMT(
g cm-3) - FMT(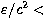 104 g cm-3). Here BBP, BPS and FMT denote equations of
state by Baym et al. (1971a), Baym et al. (1971b) and Feynman et al. (1949), respectively.
EOS G an extremely soft equation of
state. The maximum gravitational mass of a spherical neutron star for this
equation of state is
104 g cm-3). Here BBP, BPS and FMT denote equations of
state by Baym et al. (1971a), Baym et al. (1971b) and Feynman et al. (1949), respectively.
EOS G an extremely soft equation of
state. The maximum gravitational mass of a spherical neutron star for this
equation of state is 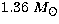 , so this EOS is not acceptable as
a realistic candidate for the true EOS of neutron star matter. It is
used in this comparison, because it is close to the softest possible
realistic EOS consistent with observational constraints. The density
range is from
, so this EOS is not acceptable as
a realistic candidate for the true EOS of neutron star matter. It is
used in this comparison, because it is close to the softest possible
realistic EOS consistent with observational constraints. The density
range is from 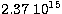 g cm-3 to 7.23
1015 g cm-3. Crystallization of neutrons is included. The
interaction is non-relativistic and represented by the modified Reid
soft core potential. This equation of state is joined to the composite
PC(
g cm-3 to 7.23
1015 g cm-3. Crystallization of neutrons is included. The
interaction is non-relativistic and represented by the modified Reid
soft core potential. This equation of state is joined to the composite
PC(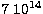 g cm
g cm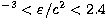 1015 g cm-3) - BBP(
1015 g cm-3) - BBP(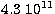 g cm
g cm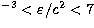 1014 g cm-3) - BPS(104 g
cm
1014 g cm-3) - BPS(104 g
cm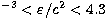 1011g cm-3) -
FMT(
1011g cm-3) -
FMT(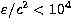 g cm-3). Here PC denotes the
equation of state by Pandharipande (1971).
EOS L is an extremely stiff
EOS. The maximum gravitational mass of a spherical neutron star for
this equation of state is
g cm-3). Here PC denotes the
equation of state by Pandharipande (1971).
EOS L is an extremely stiff
EOS. The maximum gravitational mass of a spherical neutron star for
this equation of state is 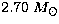 . The density range is
larger than
. The density range is
larger than 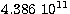 g cm-3. Compositions consist
of neutrons. The interaction is assumed non-relativistic and is
represented by the nuclear attraction due to scalar particle exchange.
This equation of state is joined to the BPS (104 g cm
g cm-3. Compositions consist
of neutrons. The interaction is assumed non-relativistic and is
represented by the nuclear attraction due to scalar particle exchange.
This equation of state is joined to the BPS (104 g cm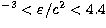 1011 g cm-3) -
FMT(
1011 g cm-3) -
FMT(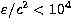 g cm-3).
EOS WFF3 (Wiringa
et al. 1988) is of intermediate stiffness. At present, the WFF3 equation of
state is regarded as one of the best candidates for the high density region.
This EOS is an improved version of the equation of state by Friedman
& Pandharipande (1981). The nucleon-nucleon interaction described by
a two-body Urbana UV14 potential and the phenomenological
three-nucleon TNI interaction are taken into account. Compositions are
considered to be neutrons. The maximum gravitational mass of a
spherical neutron star for this equation of state is
g cm-3).
EOS WFF3 (Wiringa
et al. 1988) is of intermediate stiffness. At present, the WFF3 equation of
state is regarded as one of the best candidates for the high density region.
This EOS is an improved version of the equation of state by Friedman
& Pandharipande (1981). The nucleon-nucleon interaction described by
a two-body Urbana UV14 potential and the phenomenological
three-nucleon TNI interaction are taken into account. Compositions are
considered to be neutrons. The maximum gravitational mass of a
spherical neutron star for this equation of state is 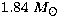 .Although the usual WFF3 EOS is joined to EOS NV (Negele & Vautherin
1973), we will also use a different version, in which it is joined to
the more modern FPS EOS (Lorenz et al. 1993).
This EOS
is also a modern version of the equation of state by Friedman &
Pandharipande (1981). The nucleon-nucleon interaction described by a
two-body Urbana UV14 potential and the phenomenological
three-nucleon TNI interaction are taken into account. In the FPS
equation of state the Skyrme model is used, where the effective
interaction has the spatial character of a two-body delta function
plus derivatives. The FPS equation of state can be considered to be
an improved version of the BBP equation of state in the region of the
lower density.
As an extreme case,
we consider an equation of state which consists of a causal limit EOS
(
.Although the usual WFF3 EOS is joined to EOS NV (Negele & Vautherin
1973), we will also use a different version, in which it is joined to
the more modern FPS EOS (Lorenz et al. 1993).
This EOS
is also a modern version of the equation of state by Friedman &
Pandharipande (1981). The nucleon-nucleon interaction described by a
two-body Urbana UV14 potential and the phenomenological
three-nucleon TNI interaction are taken into account. In the FPS
equation of state the Skyrme model is used, where the effective
interaction has the spatial character of a two-body delta function
plus derivatives. The FPS equation of state can be considered to be
an improved version of the BBP equation of state in the region of the
lower density.
As an extreme case,
we consider an equation of state which consists of a causal limit EOS
(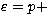 constant) for
constant) for  g cm-3 and the FPS EOS below that density. The causal
limit EOS has the property that, in the interior of the star, the phase
velocity of sound is equal to the velocity of light in vacuo, i.e.
g cm-3 and the FPS EOS below that density. The causal
limit EOS has the property that, in the interior of the star, the phase
velocity of sound is equal to the velocity of light in vacuo, i.e.
 .
.


Up: Construction of highly accurate
Copyright The European Southern Observatory (ESO)
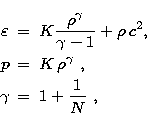
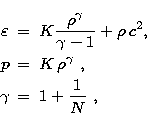
![]() constant, when
constant, when ![]() (N=0). The constant density models are also called homogeneous models.
For polytropes of index N<1.0, the density does not go to zero smoothly
at the surface and the first derivatives of the density across the surface are discontinuous.
This kind of discontinuity may become the cause of unfavorable behavior
of solutions, unless it is treated carefully. For constant density models, the
situation is even worse, since the density itself is discontinuous across the surface.
(N=0). The constant density models are also called homogeneous models.
For polytropes of index N<1.0, the density does not go to zero smoothly
at the surface and the first derivatives of the density across the surface are discontinuous.
This kind of discontinuity may become the cause of unfavorable behavior
of solutions, unless it is treated carefully. For constant density models, the
situation is even worse, since the density itself is discontinuous across the surface.
![]() polytrope),
they are helpful to check numerical codes. Since the
hydrostationary equation can be analytically integrated and no
additional numerical errors arise in solving it.
polytrope),
they are helpful to check numerical codes. Since the
hydrostationary equation can be analytically integrated and no
additional numerical errors arise in solving it.