We will compare three different codes, which follow the KEH scheme, developed by Komatsu et al. (1989a,b) for general relativistic polytropes with uniform and differential rotation and improved by Cook et al. (1992, 1994a,b) and the BGSM scheme due to Bonazzola et al. (1993).
Concerning the KEH scheme, for the present comparison, we will use the original KEH code, KEH(OR), and the KEH code by Stergioulas & Friedman (1995), KEH(SF), which follows the Cook et al. (1992, 1994a,b) modification of the KEH scheme.
In this section the three different numerical codes are briefly described. Details of these codes can be found in Komatsu et al. (1989a,b) and in Eriguchi et al. (1994) for the KEH(OR) code, in Stergioulas & Friedman (1995) for the KEH(SF) code and in Bonazzola et al. (1993) for the BGSM code.
Komatsu et al. (1989a) have developed a new scheme for solving rapidly
rotating relativistic stars. The Einstein equations for three metric
potentials ![]() and
and ![]() are transformed into integral equations
by using appropriate Green's functions for the elliptical type differential
operators. In principle, one can choose Green's functions which decrease
as 1/r or more rapidly at large distances. Consequently boundary conditions
at infinity, i.e. asymptotically flat conditions can be easily included
in the integral equations. It is noted that in this integral representation
the integrand contains the metric and the matter quantities such as
the energy density and the pressure. The fourth metric
are transformed into integral equations
by using appropriate Green's functions for the elliptical type differential
operators. In principle, one can choose Green's functions which decrease
as 1/r or more rapidly at large distances. Consequently boundary conditions
at infinity, i.e. asymptotically flat conditions can be easily included
in the integral equations. It is noted that in this integral representation
the integrand contains the metric and the matter quantities such as
the energy density and the pressure. The fourth metric ![]() obeys a
first order partial differential equation which can be easily
integrated, if the other metric potentials are known. The domain of integration
is truncated at a finite distance from the star (roughly twice the equatorial radius)
and the metric potentials
in the integrands
are assumed to vanish at that finite distance (instead
of at infinity).
obeys a
first order partial differential equation which can be easily
integrated, if the other metric potentials are known. The domain of integration
is truncated at a finite distance from the star (roughly twice the equatorial radius)
and the metric potentials
in the integrands
are assumed to vanish at that finite distance (instead
of at infinity).
The KEH scheme is the extended version of the self-consistent-field
(SCF) scheme which was developed for solving Newtonian rotating stars
(Ostriker & Mark 1968; Hachisu
1986) and applied to relativistic rotating stars by Bonazzola
& Schneider (1974) with a choice of metric functions different from that of
the codes considered in this article. In the SCF method, the iteration
proceeds as follows. If one assumes initial guesses for the matter
quantities and the metric potentials, new (and better) values for ![]() and
and ![]() can be obtained using the integral representations for
the metric potentials The fourth metric potential
can be obtained using the integral representations for
the metric potentials The fourth metric potential ![]() can be easily
solved as mentioned before. By using newly obtained metric
potentials, a new density and a new pressure can be computed from the
hydrostationary equilibrium Eq. (8). One needs to
repeat the same procedure until the relative differences between the
newly obtained quantities and the old ones become less than a certain
small number, typically 10-5.
can be easily
solved as mentioned before. By using newly obtained metric
potentials, a new density and a new pressure can be computed from the
hydrostationary equilibrium Eq. (8). One needs to
repeat the same procedure until the relative differences between the
newly obtained quantities and the old ones become less than a certain
small number, typically 10-5.
In the original KEH code, the ratio of the central pressure (![]() )
to the central energy density (
)
to the central energy density (![]() ),
),
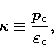 |
(9) |
The KEH(SF) code (Stergioulas & Friedman 1995) differs from the
original KEH scheme in two ways. First, it follows Cook et al.
(1992) in using a redefined radial variable
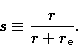 |
(10) |
Second, Stergioulas & Friedman found that the choice of coordinates
in the original KEH scheme results in the metric potential ![]() oscillating in the radial direction. The oscillation is especially
pronounced inside the star and introduces an error of
oscillating in the radial direction. The oscillation is especially
pronounced inside the star and introduces an error of ![]() in the
mass, radius and other quantities. The problem was fixed by using a
finite difference formula for the second order radial derivative that
uses twice the grid-spacing. Although this formula is, in principle, of
lower accuracy, the oscillations are damped completely, resulting in
a more accurate stellar model.
in the
mass, radius and other quantities. The problem was fixed by using a
finite difference formula for the second order radial derivative that
uses twice the grid-spacing. Although this formula is, in principle, of
lower accuracy, the oscillations are damped completely, resulting in
a more accurate stellar model.
The KEH(OR) code used in this comparison has been modified so as to
use the same second order derivative formula as Stergioulas &
Friedman, to smooth out the oscillations in the metric potential
![]() .
.
Bonazzola et al. (1993) have developed a new formulation based on the 3 + 1 formalism which has been used in hydrodynamics in general relativity. Their choice of slicing and gauge in the 3 + 1 formalism results in the same form of the metric usually chosen for stationary problems, i.e. (2). Consequently the Einstein equations are reduced to the same differential equations of elliptic type as used by other schemes.
The main part of the BGSM formulation is similar to that of the KEH
formulation, except for the metric coefficient ![]() for
which a second-order (elliptic) equation is used instead of a
first-order equation in KEH. The Einstein equations are reorganized
so as to "pick" out the Laplacian operators in two and three dimensional
flat spaces and regard all other remaining terms as "source terms" in
the Poisson-like equations in two and three dimensional flat spaces.
Concerning the matter, essentially the same equation as (8)
is used for the hydrostationary equation.
for
which a second-order (elliptic) equation is used instead of a
first-order equation in KEH. The Einstein equations are reorganized
so as to "pick" out the Laplacian operators in two and three dimensional
flat spaces and regard all other remaining terms as "source terms" in
the Poisson-like equations in two and three dimensional flat spaces.
Concerning the matter, essentially the same equation as (8)
is used for the hydrostationary equation.
The characteristic features of the BGSM code can be found in the numerical solving method, i.e. the pseudo-spectral method (Gottlieb & Orszag 1977; Bonazzola et al. 1996, 1997, 1998b). In the spectral method all functions are expanded in terms of certain base functions and algebraic equations for coefficients which appear in the expansion are solved. Therefore there are two distinct procedures in this method: one is obtaining coefficients from the functions and the other is constructing functions by using the coefficients. Since these two steps need to be, in general, performed many times, it is highly desirable to use a fast algorithm. In the spectral method of the BGSM code, Bonazzola et al. (1993) have adopted trigonometric functions for the angle variable and the Chebyshev polynomials for the radial variable. Consequently for the angle part of any function, the fast fourier transform (FFT) can be employed. Concerning the radial variable, a new variable which is related to the radial variable by a simple equation is introduced so that the Chebyshev polynomials are expressed by the trigonometric functions. After this transformation, one can use the FFT also for the radial variable.
The BGSM code can handle the region extended to infinity as is done by
the KEH(SF) code. This can be performed by
introducing a new radial variable u as follows:
 |
(11) |
It may be fair to note that in the Newtonian rotating star problems a similar expansion was used by Ostriker & Mark (1968) in the SCF method, although Ostriker and Mark used the integral form of the Newtonian potential instead of solving the Poisson equation directly and they did not use the FFT.
Here we summarize similarities and difference between the three codes:
A) Common features through all three codes:
B) The KEH(OR) code differs from the other two codes in that the boundary conditions are not applied at infinity, but approximate boundary conditions are applied at a finite distance from the star.
C) A difference between the BGSM code and the other codes is the use of a
second-order (elliptic)equation for ![]() in BGSM versus a first-order equation for
in BGSM versus a first-order equation for
![]() in KEH.
in KEH.
We reorganized our codes so as to make the differences as small as possible. The codes agree exactly on:
Since the three codes use different grids and/or numerical methods for solving the field equations, there will always be a residual difference in the results, even after this reorganization. This residual difference is what we want to determine.
Values used in this paper for the velocity of light c,
the gravitational constant G, the mass of the sun ![]() and
the baryon mass
and
the baryon mass ![]() are as follows:
are as follows:
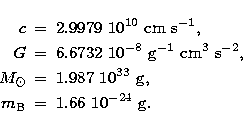 |
||
For realistic equations of state, the energy density, pressure and other thermodynamical quantities are given in tables. Intermediate values need to be obtained by a method of interpolation. We will use two different interpolation schemes, the four-point Lagrange interpolation (hereafter LI) and the cubic Hermite interpolation (HI) (Swesty 1996):
A) Lagrange interpolation.
Let us assume that there is a table which relates the variable x
to the variable y at n points, i.e. a set of values (xi, yi)
for ![]() are tabulated.
For the LI scheme the interpolated formula
are tabulated.
For the LI scheme the interpolated formula ![]() can be expressed as
can be expressed as
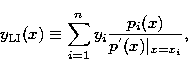 |
(12) |
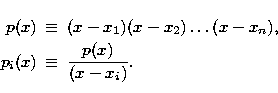 |
(13) | |
| (14) |
B) Hermite interpolation.
In the Hermite interpolation, the interpolated formula ![]() for
for ![]() is expressed as
is expressed as
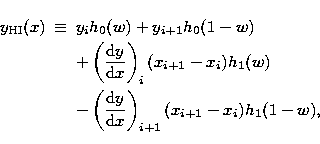 |
||
| (15) |
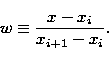 |
(16) |
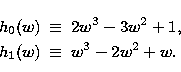 |
(17) | |
| (18) |
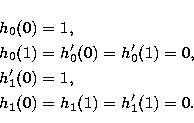 |
(19) | |
| (20) | ||
| (21) | ||
| (22) |
Copyright The European Southern Observatory (ESO)