4 Source counts

Since the 1960s it has been recognized that counts of radio sources can provide important cosmological information, especially about the evolution of radio sources. Identification and source counts statistics indicated that radio sources were preferentially located in early epochs of the universe (Longair 1966). Recently, several authors (Readhead et al. 1996; Fanti et al. 1995; O'Dea et al. 1997) have shown that if GPS and CSS sources evolve into large scale FRI/FRII radio sources, they must significantly decrease in radio luminosity (a factor 10 to 30) to account for the high number of GPS and CSS sources compared to the number of FRI and FRII radio galaxies. In this section the GPS source counts at faint flux densities derived from our faint sample are constructed and discussed.

To be able to derive the GPS source counts from the sample, the intrinsic distribution of GPS sources with peak frequency and peak flux density has to be determined. The observed distribution of peak flux densities and peak frequencies of the GPS sources in our sample is shown in Fig. 6. The diamonds represent the sources initially selected on the basis of their 325 - 5000 MHz spectral index, the squares represent the sources selected on their 325 - 609 MHz spectral index, while the filled squares represent the sources selected from the 325 - 609 MHz comparison which also would have been in the sample if selected on their 325 - 5000 MHz spectral index. It should be noted that Fig. 6 is the observed distribution, and that the selection criteria are a function of peak frequency, peak flux density, and optically thin and thick spectral indices of the sources, making statistical studies complicated.

Whether a GPS source with a certain peak flux density and peak frequency will appear in our sample depends on its optically thin and thick spectral indices. If the optically thick spectral index is too inverted, the 325 MHz flux density is too low to be in the sample. If the optically thin spectral index is too steep, then the 325 - 5000 MHz spectral index will not be inverted. The range of optically thick and thin spectral indices allowed for a GPS source to appear in the sample is a strong function of peak frequency and peak flux density. To be able to derive the parent distribution of peak flux densities and peak frequencies of GPS sources from the observed distribution in our sample, the fraction of GPS sources selected as a function of peak flux density and peak frequency has to be estimated.

We assume that the peak frequency, peak flux density and the optically thin and thick spectral indices are independent of each other. The intrinsic distribution of optically thin and thick spectral indices have to be determined from their observed distributions. The normalized spectra (in both frequency and flux density) of the sources in our sample are plotted in Fig. 7. The solid line represents the best fit of equation 1 to the data, which gives optically thin and thick spectral indices of -0.75 and +0.80 respectively.

 

Figure 6:   The distribution of peak frequencies and peak flux densities for the GPS sources in our sample. The diamonds represent the sources selected on their 325 - 5000 MHz spectral index; the squares represent the sources selected on their 325 - 609 MHz spectral index; the filled squares represent the sources selected from the 325 - 609 MHz comparison which also would have been in the sample if selected on their 325 - 5000 MHz spectral index. The dotted lines represent the limits for which a GPS source with optically thin and optical thick spectral indices of -0.75 and +0.80 respectively would be selected on the basis of its 325 - 5000 MHz spectral index. The arrow indicates the lower limit for the peak frequency and peak flux density of B1945+6024

If we assume the intrinsic or parent spectral index distributions to be Gaussian functions with means and standard deviations of -0.75 and 0.15 (thin) and +0.80 and 0.18 (thick), then the observed spectral index distributions are recovered after applying the selection effects to the parent spectral index distributions. Although the outcome of this is not very accurate, this is not too important since our main concern is too show that no significant fraction of GPS sources was missed; sources with highly inverted spectral indices of 2, say, are unlikely to be included unless the peak flux density is high and the peak frequency is low enough. Sufficient numbers of these sources could have an effect on the parameters of the optically thick spectral index distribution.

 

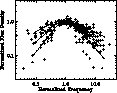Figure 7:   The spectra of the GPS sources normalized (scaled) in both frequency and flux density. The solid line represents the best fit of equation 1 to the data, which gives optically thick and thin spectral indices of respectively +0.80 and -0.75. The dashed lines represent optical thick and thin spectral indices of +0.5, +1.1, -0.5 and -1.0

To obtain an indication of the number of sources with very inverted spectra ($\alpha_{\rm thick} \gt 1.1$), we looked for highly inverted GPS sources in our sample with peak frequencies lower than 2 GHz and peak flux densities greater than 100 mJy, because these will be the least influenced by selection effects on the optically thick spectral index. Only one object out of ten (10%) was found to have an optically thick spectral index greater than 1.1, while 5% would be expected from the distribution of optically thick spectral indices. Hence we regard any missed population of GPS sources with very steep optically thick spectral indices as small and negligible.

The GPS sources in our sample which have a flux density at 325 MHz >25 mJy and an inverted spectral index between 325 and 5000 MHz have been used to determine the peak frequency and peak flux density number distributions. The sample is divided into bins of peak flux density of 50 - 100 mJy, 100 - 200 mJy and 200 - 400 mJy and bins of peak frequency of 1 - 2 GHz, 2 - 4 GHz and 4 - 8 GHz. If it is assumed that the parent population of GPS sources has spectral index distributions as described above, then for each bin the percentage of GPS sources selected in our sample can be determined. For each bin, the number of sources in the parent population of GPS sources was estimated by dividing the number of GPS sources in the sample which fall in the bin by these percentages which were between 40% and 100%.

The observed number of GPS sources, corrected for selection effects as above, have been summed in peak frequency space to determine the surface density of GPS sources as function of flux density. The source counts for the three flux density bins, normalized by the flux density to the power 2.5 are plotted as squares in Fig. 8 (a horizontal relation is expected for a uniformly distributed Euclidean space). The triangles represent the observed surface density counts, not corrected for selection effects, which is a good lower limit. We have used the well defined sample of De Vries et al. (1997) compiled from the working sample of GPS sources from O'Dea et al. (1991) to determine the surface density of GPS sources at high flux density. We determined the number of GPS sources in the de Vries et al. sample which lie within the Pearson and Readhead survey region (Pearson & Readhead 1988, $\delta \gt 35 ^{\circ}$, $\vert b \gt 10^{\circ}\vert$, 2.0 sr), having peak frequencies between 1 and 8 GHz and flux densities between 2 and 6 Jy. There are five objects satisfying these criteria, which leads to a normalized surface density count of $22\ \pm \ 10\,{\rm Jy}^{-3/2} {\rm Sr}^{-1}$ in this flux density range, assuming that the spectra of all the radio sources in this region brighter than 2 Jy are well known and that therefore this sample of GPS sources is complete. This measurement is indicated by the diamond symbol in Fig. 8.

Several authors (e.g. Fanti et al. 1995; Readhead et al. 1996; O'Dea et al. 1997) have proposed that GPS sources may evolve into large size FRI/FRII radio sources. Therefore it is interesting to compare the GPS source counts with source counts of FRI/FRII radio sources. It is not very useful to compare them directly to the total radio source counts at comparably high frequency, because these are dominated by compact flat spectrum sources, which are probably not related to GPS sources in an evolutionairy way. However, it can be assumed that the WENSS source counts at 325 MHz are dominated by the large size radio source population, because they have in general steep ($\alpha <-0.5$) spectra. The radio source counts at 325 MHz from the WENSS mini-survey region (Rengelink et al. 1997) is shown in Fig. 8 by the dotted line. Note the resemblance between the shape of this curve and the data for the GPS sources (squares + diamond). The median spectral index is about -0.85, which we used to estimate the source counts for large scale radio sources at higher frequencies comparable to the peak frequencies of the GPS sources. Note that the source counts of the GPS sources are not at a certain fixed frequency, but resemble the distribution of peak flux densities. However, we assume that within the errors the distribution of the peak flux densities of the GPS sources in our sample is the same as for the flux densities at the median peak frequency, which is 2 GHz. We determined the large size radio source number counts at 2 GHz from the 325 MHz counts of the WENSS mini-survey region, assuming a fixed spectral index of -0.85. This is represented by the solid curve in Fig. 8.

How can the differences in number counts between the GPS sources and large scale radio sources be interpreted? If GPS sources evolve into large scale radio sources, it is reasonable to assume that they undergo the same cosmological evolution, because the typical lifetime of a radio source is significantly smaller than cosmological time-scales. Assuming that the slope of the luminosity function of GPS sources is identical to the slope of the luminosity function of large size radio sources and that all GPS sources evolve into large size radio sources, one could obtain the ratio of the life time of the two classes of radio source and the luminosity evolution of the GPS sources. If a radio source is 10 times brighter in its GPS phase than in its FRI/FRII phase, and if the time scale of the GPS phase is 250 times shorter than the age of large scale radio sources, then the dashed line is expected for the source counts of GPS sources. Namely in that case the curve for FRI/FRII radio sources moves a factor 250 down due to the age difference, and a factor of 10 to the right and a factor factor 10^3/2 upward due to the luminosity evolution. This agrees quite well with the observed GPS source counts.

 

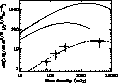Figure:   The number counts of GPS sources as function of peak flux density. The squares are from the data in this paper. The triangles are the observed, not corrected, source counts. The point indicated by the diamond is derived from de Vries et al. (1997). The dotted line represents the WENSS radio source counts at 325 MHz in the mini-survey region, and the solid line are these source counts corrected to 2 GHz using a spectral index of -0.85 (see text). The dashed line is the curve for 1/250 of the 2 GHz counts shifted a factor 10 upward in flux density. This is consistent with the data

However, this straightforward interpretation is probably too simplistic. Firstly, the redshift distributions of GPS galaxies and large size radio sources are not the same, which indicates that the slopes of their luminosity functions are different (see Snellen 1997). This has consequences for the interpretation of the radio source counts of GPS sources. It should be investigated if a simple radio source evolution model, as for example presented in Snellen (1997), combined with the cosmological evolution of the radio luminosity function for large size radio sources, is consistent with the GPS source counts presented here. This is beyond the scope of this paper. Secondly, the GPS source counts presented here also include the GPS quasars, although it is not clear that they are related to the GPS galaxies. Excluding the GPS quasars, which contribute about one third of the members of both the bright and faint GPS samples, shifts the squares and the diamond in Fig. 8 down by a factor 1.5. In this case, the number counts are consistent with radio galaxies in the GPS phase being 10 times brighter for a period $\sim 400$ times shorter than the FRI/FRII phase.