4 Other types of fit

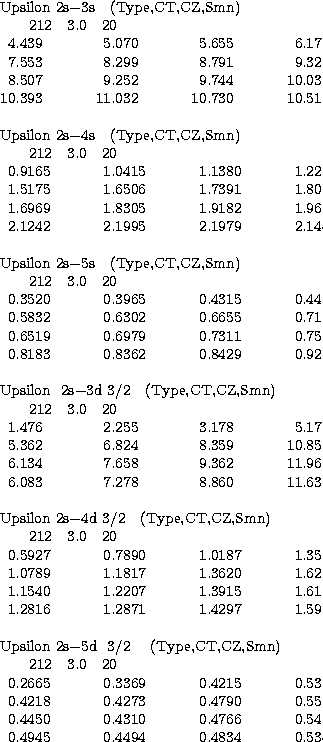
As well as the standard 5-point cubic spline fit, the new program OmeUpZ allows the options of varying the number of nodal points, and of using quadratic splines (in which case the knots are at mid-nodal points) or Tchebyshev polynomials.

In general, global fits with Tchebyshev polynomials are not suitable for this type of data, especially if resonance contributions are appreciable. For such data, piecewise fits with low-degree splines are more appropriate, and in extreme cases it may be best to resort to linear splines (see B&T Sect. 6.2).

  

Table 5: Program data to obtain ${\sl \Upsilon}$ for charges $8\leq Z_0 \leq 30$

 

Table 5: continued

However, Tchebyshev fits are very useful for other types of data which might be expected to have a convergent power series expansion over the whole range. The ZSF data is very smooth so, as an example of using the program in this mode, we also give results obtained from 4-point Tchebyshev fits to ${\sl \Upsilon}_{\rm rr}$. For these, the interpolation function ${\rm poly4}(P_1,P_2,P_3,P_4,X)$ is used in place of ${\rm spline}(P_1,P_2,P_3,P_4,P_5,X)$, both these functions being defined in terms of FORTRAN listings in the Appendix. This gives an even more compact representation of the data, and still to about 1% accuracy provided the range of nuclear charge is limited to $8\leq Z_0 \leq 30$, which covers most cases of astrophysical interest. The results are given in Table 5.

  

Table 6: $\sl \Upsilon({\rm 2s_{1/2} - 3s_{1/2}})$: Comparison of results for Fe$^{+23}\,$. ZSF(5), present 5-point spline fit; ZSF(4), present 4-point Tchebyshev fit; IRON, from the IRON Project (Berrington & Tully 1997)

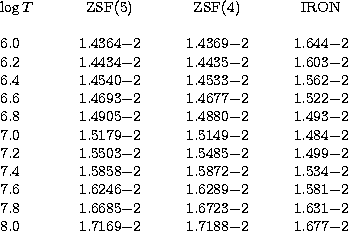As an example to compare with we have run the interactive program described in the Appendix for the case of the $\rm 2s \to 3s$ transition in $\rm Fe^{+23}$. In Table 6 we give the corresponding ${\sl \Upsilon}$ as a function of logT. The column headed ZSF(5) has results obtained by using as input to the interactive program the spline data in Table 4. The numbers in Col. ZSF(4) are obtained in a similar way but using the Tchebyshev data given in Table 5. In the final column of Table 6 we give results from the IRON Project (see Berrington & Tully 1997). There is good agreement for most of the temperatures in the table although at the lowest ones the IRON results clearly exceed those of ZSF(5) and ZSF(4). This is explained by the effect of resonances which Berrington & Tully take account of whereas ZSF do not. Most of the collision strengths considered by Berrington & Tully are greatly modified by resonances at relatively low energies. As a result of this the resonances only have a strong effect on the thermally averaged collision strengths at temperatures which are well below those of astrophysical importance, i.e. where $\rm Fe^{+23}$ is expected to be abundant under conditions of coronal ionization equilibrium. Another small difference can be seen to occur at the highest temperature where the ZSF results exceed those of the IRON Project by a few percent. This is explained by the fact that ZSF's calculation is fully relativistic and therefore takes account of both the magnetic effects and the Lorentz transformation of electron velocities mentioned in Sect. 1.1 of B&T. On the other hand the IRON Project calculation allows only for the magnetic effects but treats the kinematics of the collision classically. A proper relativistic treatment of the colliding electron's velocity can profoundly modify the collision strength at high energies and hence affect ${\sl \Upsilon}$ at high temperatures.