

Up: Forbidden transitions in Li-like
Subsections
We use notation as established in B&T. All the transitions
treated in the present paper are of type 2. In this section we specify the changes
required for these transitions as a consequence of including relativistic
effects. We use the same equation numbers as in B&T, with * added to
the number of the modified equation. Derivations, and details for other
types of transition, will be given elsewhere.
In order to distinguish the adjustable parameter C occurring in the
different fits we denote it by CE, CT, CZ according to whether the
fit is over the range of energy E, temperature T or ion charge Z.
Equation (9) of B&T is unchanged except that C is denoted by
CE, but (10) becomes
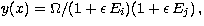 (10*)
(10*)
where 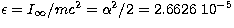 ,
,
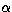 being the fine structure constant.
being the fine structure constant.
We use the interactive FORTRAN program BORN written by
Burgess (1998) to compute the non relativistic high energy limit
points presented in Table 1.
Table 1:
High energy Born collision strengths
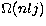 for transitions
for transitions 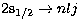
|
|
We take radial orbitals 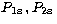 from
Clementi & Roetti (1974) and calculate
from
Clementi & Roetti (1974) and calculate 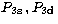 ,
,
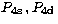 ,
, 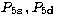 using Hibbert's (1975) program CIV3. The parameterised form of Pnl(r)
is
using Hibbert's (1975) program CIV3. The parameterised form of Pnl(r)
is
![\begin{displaymath}
P_{nl}(r) = \sum_{p=1}^kc_{nlp} \Bigl[{{(2\zeta_{nlp})^{2q_{...
..._{nlp})!}}\Bigr]^{1/2}r^{q_{nlp}}\exp(-\zeta_{nlp} r). \eqno(1)\end{displaymath}](/articles/aas/full/1998/13/ds1463/img22.gif)
Our choice for the integers 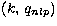 in Eq. (1) is
in Eq. (1) is
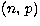 for l = 0 and
for l = 0 and 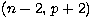 for l = 2. Results for four ions
in the sequence, namely Z0 = 8, 16, 26, 36, are given in Table 2.
for l = 2. Results for four ions
in the sequence, namely Z0 = 8, 16, 26, 36, are given in Table 2.
Table 2:
Radial orbital parameters 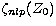 and
cnlp(Z0)
and
cnlp(Z0)
|
|
We
obtained the values for
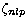 and cnlp by using CIV3 to minimise the
and cnlp by using CIV3 to minimise the 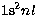 term energy. Since in general many local minima exist it can be quite an
arduous task locating the one that seems to be the lowest. A similar
investigation has in the past been carried out for some of the orbitals
included here (see Tully et al. 1990
and Berrington & Tully 1997).
A comparison of the present and past data shows that they are not always the
same. Although we have not compared the orbitals it is our belief that they do
not differ significantly. The numerical differences alluded to here reflect the
fact that in the present work we have given greater attention to locating the
term minima than in the past. In all cases we use the minimization code
MODDAV by setting the CIV3 parameter IDAVID = 0. We assume each orbital
Pnl to have the minimum number of exponents dictated by nl and
therefore the coefficients cnlp are determined by the conditions of
orthonormality, but for convenience we include their numerical values in
Table 2.
It is extremely useful, when fitting collision data along an
entire isoelectronic sequence, to have an indication of the behaviour of
the collision strengths when Z becomes large. The true limiting values do
not exist since the relativistic wave functions for the ion collapse when
Z is too large (e.g. for s-states, when
term energy. Since in general many local minima exist it can be quite an
arduous task locating the one that seems to be the lowest. A similar
investigation has in the past been carried out for some of the orbitals
included here (see Tully et al. 1990
and Berrington & Tully 1997).
A comparison of the present and past data shows that they are not always the
same. Although we have not compared the orbitals it is our belief that they do
not differ significantly. The numerical differences alluded to here reflect the
fact that in the present work we have given greater attention to locating the
term minima than in the past. In all cases we use the minimization code
MODDAV by setting the CIV3 parameter IDAVID = 0. We assume each orbital
Pnl to have the minimum number of exponents dictated by nl and
therefore the coefficients cnlp are determined by the conditions of
orthonormality, but for convenience we include their numerical values in
Table 2.
It is extremely useful, when fitting collision data along an
entire isoelectronic sequence, to have an indication of the behaviour of
the collision strengths when Z becomes large. The true limiting values do
not exist since the relativistic wave functions for the ion collapse when
Z is too large (e.g. for s-states, when 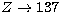 ). Nevertheless, the
non-relativistic values, scaled by a factor (Z+1)2, do exist in the
limit and are useful in this context.
). Nevertheless, the
non-relativistic values, scaled by a factor (Z+1)2, do exist in the
limit and are useful in this context.
D. H. Sampson and his co-workers have, over the past two decades, produced
an enormous amount of reliable collision data in just this limit, and we
make use of their Coulomb Born Oppenheimer results for the hydrogenic
transitions 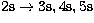 and
and 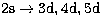 . These are
available in Golden et al. (1981)
and Clark et al. (1982). However it
should be noted that the values they tabulate for the collision strength
need to be multiplied by a factor 2 in order to be consistent with the
definitions of
. These are
available in Golden et al. (1981)
and Clark et al. (1982). However it
should be noted that the values they tabulate for the collision strength
need to be multiplied by a factor 2 in order to be consistent with the
definitions of 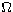 and statistical weight given in equations (2)
and (3) in Golden et al. (1981).
and statistical weight given in equations (2)
and (3) in Golden et al. (1981).
We have made only approximate allowance for the relativistic corrections to
these limiting values. However, the uncertainties arising from this affect
only values beyond the range of the ZSF tabulation (i.e. for Z > 89 or
Ej > 104 Ryd, T > 109). Further work on this will be given elsewhere.
The definition of 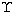 in terms of
in terms of 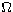 ,
Eq. (21) of B&T, is unchanged, (as is the detailed
balance Eq. (22)), so that the OmeUpZ
program can be used to calculate
,
Eq. (21) of B&T, is unchanged, (as is the detailed
balance Eq. (22)), so that the OmeUpZ
program can be used to calculate 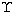 from the fitted
from the fitted 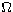 as described in Sects. 6.3 and 7.2 of B&T.
However, Eq. (20) for the rate coefficient is altered by replacing the
factor
as described in Sects. 6.3 and 7.2 of B&T.
However, Eq. (20) for the rate coefficient is altered by replacing the
factor 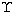 , on the right hand side, by
, on the right hand side, by
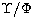 , where
, where
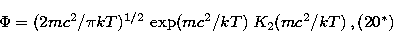
K2 being a modified Bessel function
(Abramowitz & Stegun 1965). This
result is for a low density, high temperature plasma corresponding to the
nondegenerate Maxwell-Juttner case discussed by Chandrasekhar
(1957, pp. 394-8).
Except for very large values of T, we have
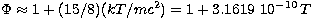 .
.
Equation (27) of B&T is unchanged except that C is denoted by
CT, but (28) becomes
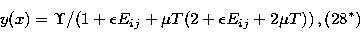
where 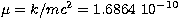 .
As described in Sects. 7.5 and 8.2 of B&T, for a given
transition, the standard 5-point cubic spline fitting procedure produces
5 nodal values of
.
As described in Sects. 7.5 and 8.2 of B&T, for a given
transition, the standard 5-point cubic spline fitting procedure produces
5 nodal values of 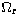 or
or 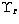 for each Z,
which may themselves then be fitted as a function of a reduced Z variable,
so as to produce the doubly reduced quantities
for each Z,
which may themselves then be fitted as a function of a reduced Z variable,
so as to produce the doubly reduced quantities 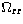 or
or
 . As in B&T, use of a common value of CE or CT
for all the values of Z is obviously most convenient and leads to no
significant loss of accuracy.
. As in B&T, use of a common value of CE or CT
for all the values of Z is obviously most convenient and leads to no
significant loss of accuracy.
Table 3:
Program data to obtain 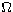 for all charges
for all charges
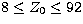
|
|
Equations (58) and (59) of B&T are unchanged except that C is denoted by
CZ.
This gives a 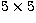 matrix Smn of nodal values of
matrix Smn of nodal values of
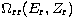 or
or 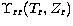 from which
from which
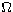 or
or 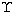 may be obtained for all energies or
temperatures and all charges.
may be obtained for all energies or
temperatures and all charges.
Values of the Smn matrix elements, together with the values of CE or
CT and CZ are given in Tables 3 and 4.
The fitted values of 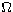 given by Table 3 were compared with all
the original tabulated values given by ZSF for these transitions (i.e. for
all 6 energies
given by Table 3 were compared with all
the original tabulated values given by ZSF for these transitions (i.e. for
all 6 energies 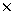 all 85 charges
all 85 charges 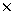 9 transitions); the rms
error was 0.3% and the maximum error was 0.9%. The rms error involved in
fitting
9 transitions); the rms
error was 0.3% and the maximum error was 0.9%. The rms error involved in
fitting 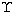 , to obtain Table 4, was also found to be about
0.3%.
, to obtain Table 4, was also found to be about
0.3%.
Table 4:
Program data to obtain 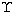 for all charges
for all charges 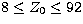
|
|
As noted in Sect. 2.3, there is some uncertainty in the values of
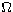 beyond the range of the ZSF tabulation. We estimate that
the resulting uncertainty in values obtained from Table 3 and 4 exceeds
1% only if Z0 > 92 or Ej > 104 Ryd, T > 109).
beyond the range of the ZSF tabulation. We estimate that
the resulting uncertainty in values obtained from Table 3 and 4 exceeds
1% only if Z0 > 92 or Ej > 104 Ryd, T > 109).


Up: Forbidden transitions in Li-like
Copyright The European Southern Observatory (ESO)
![]() (10*)
(10*)
![]() ,
,
![]() being the fine structure constant.
being the fine structure constant.
![\begin{displaymath}
P_{nl}(r) = \sum_{p=1}^kc_{nlp} \Bigl[{{(2\zeta_{nlp})^{2q_{...
..._{nlp})!}}\Bigr]^{1/2}r^{q_{nlp}}\exp(-\zeta_{nlp} r). \eqno(1)\end{displaymath}](/articles/aas/full/1998/13/ds1463/img22.gif)
![]() and
and ![]() . These are
available in Golden et al. (1981)
and Clark et al. (1982). However it
should be noted that the values they tabulate for the collision strength
need to be multiplied by a factor 2 in order to be consistent with the
definitions of
. These are
available in Golden et al. (1981)
and Clark et al. (1982). However it
should be noted that the values they tabulate for the collision strength
need to be multiplied by a factor 2 in order to be consistent with the
definitions of ![]() and statistical weight given in equations (2)
and (3) in Golden et al. (1981).
and statistical weight given in equations (2)
and (3) in Golden et al. (1981).
![]()
![]() .
.![]()
![]() matrix Smn of nodal values of
matrix Smn of nodal values of
![]() or
or ![]() from which
from which
![]() or
or ![]() may be obtained for all energies or
temperatures and all charges.
may be obtained for all energies or
temperatures and all charges.
![]() given by Table 3 were compared with all
the original tabulated values given by ZSF for these transitions (i.e. for
all 6 energies
given by Table 3 were compared with all
the original tabulated values given by ZSF for these transitions (i.e. for
all 6 energies ![]() all 85 charges
all 85 charges ![]() 9 transitions); the rms
error was 0.3% and the maximum error was 0.9%. The rms error involved in
fitting
9 transitions); the rms
error was 0.3% and the maximum error was 0.9%. The rms error involved in
fitting ![]() , to obtain Table 4, was also found to be about
0.3%.
, to obtain Table 4, was also found to be about
0.3%.
![]() beyond the range of the ZSF tabulation. We estimate that
the resulting uncertainty in values obtained from Table 3 and 4 exceeds
1% only if Z0 > 92 or Ej > 104 Ryd, T > 109).
beyond the range of the ZSF tabulation. We estimate that
the resulting uncertainty in values obtained from Table 3 and 4 exceeds
1% only if Z0 > 92 or Ej > 104 Ryd, T > 109).