

Up: Isokinetic patch measurements on
The following step is the determination of the position of the lunar
edge in each image and then the correlation between the images of the
same frame.
The edge is found column by column introducing a
coordinate, x, and a function, I(x), proportional to the intensity of the
pixels in that column (see Fig. 4(above)).
It is assumed that the edge of the Moon produces an intensity leap
higher than any other feature in the image
(except for the cut due to the edge of the CCD):
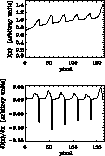 |
Figure 4:
Intensity plot in arbitrary units (above) and its derivative
(below) along one column of the CCD |
the pixel with the highest slope is then the value of x in which the
derivative 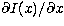 , reaches its
maximum (see Fig. 4(below)).
In order to find with better accuracy the position of the edge within
the pixel, this one and the two pixels at its sides are fitted with a
parabola.
, reaches its
maximum (see Fig. 4(below)).
In order to find with better accuracy the position of the edge within
the pixel, this one and the two pixels at its sides are fitted with a
parabola.
We have made extensive tests in laboratory with illumination conditions
similar to the one experienced during the run and we can say that
the vertex of the parabola allows one to determine the position of the edge
with a repeatability of approximately 0.07 arcsecs.
Every edge, obtained at a time t, is then
represented by a vector of 192 elements,
![$[x_{(1,t)},\dots,x_{(192,t)}]_i$](/articles/aas/full/1998/12/ds1440/img18.gif) , with
, with 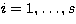 ,and every frame containing s images
is reduceded to a matrix of s rows, each row corresponding to an edge.
Rows of the same matrix are scaled in order to have the same value
in the first element, that is equivalent to say:
,and every frame containing s images
is reduceded to a matrix of s rows, each row corresponding to an edge.
Rows of the same matrix are scaled in order to have the same value
in the first element, that is equivalent to say:
| 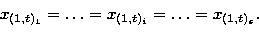 |
(3) |
The standard deviation between the s rows, column by column,
is then calculated moving along the edge, for 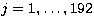 :
:
|  |
(4) |
and this is equivalent to measuring the loss of correlation in
the atmospheric induced tilt perturbations as the distance
from a reference point increases.
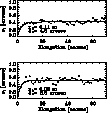 |
Figure 5:
Interpolating the data allows to obtain both the values
for 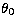 and for r0.
It can be seen the loss of correlation between tilt perturbations
for increasing distances from a reference point along the edge of the Moon.
These are two examples of the data collected during the tests.
Only one portion of the field of view, the most interesting, is plotted and for r0.
It can be seen the loss of correlation between tilt perturbations
for increasing distances from a reference point along the edge of the Moon.
These are two examples of the data collected during the tests.
Only one portion of the field of view, the most interesting, is plotted |
Forcing all the edges in the same image
to have the same value in the first pixel,
introduces a multiplicative factor, 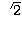 , that has
to be considered when determining the value of
, that has
to be considered when determining the value of 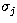 .The multiplicative factor arises because the variance of the first
pixel,
.The multiplicative factor arises because the variance of the first
pixel, 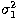 , sums quadratically with the absolute
variance of each other
pixel,
, sums quadratically with the absolute
variance of each other
pixel, 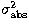 , that is equivalent to say:
, that is equivalent to say:
| 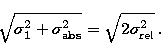 |
(5) |
Plotting the standard deviation versus the distance
from the reference position this loss of correlation
is clearly visible (see Fig. 5).
In these examples, over a distance of the order of less than 5
arcsec, the correlation
is completely lost and the data show statistical oscillations
around a mean value, 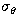 .This residual scatter is due both to Poissonian statistic, because of
the limited number of edges collected in each image, to the photometric
noise (including read out and photon shot noise) and finally
to inhomogeneities in sensitivity of the pixels.
.This residual scatter is due both to Poissonian statistic, because of
the limited number of edges collected in each image, to the photometric
noise (including read out and photon shot noise) and finally
to inhomogeneities in sensitivity of the pixels.
In order to find the value of 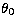 , that is the value for
which the correlation decreases of a factor
, that is the value for
which the correlation decreases of a factor 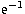 ,we fitted the data with the following function:
,we fitted the data with the following function:
| ![\begin{displaymath}
f(\theta) = \sqrt{2} \sigma_\theta \left[1-
\exp \left( -{\theta \over \theta_0 } \right) \right].\end{displaymath}](/articles/aas/full/1998/12/ds1440/img32.gif) |
(6) |
However, it can be noted from one of the data plots,
that this is only a rough
approximation of the expected theoretical behaviour
(Valley & Wandzura 1979).
In fact, sometimes one can observe at moderate angular distances an
anticorrelation between the tilt perturbations
and this is due to the fact that what is measured is not
just the tilt component but instead it is the sum of both tilt and coma
of any order.
Although we did not measure the anticorrelation because we
had not enough samples to obtain a reliable estimate,
it must be noted that knowing the amount of anticorrelation
can be used to have a comparison between the observed turbulence
power spectrum and that of Kolmogorov.
When the anamorphic relay is used to increase
the size of the field of view
it is possible, in principle, to increase the precision
in the measurement of 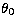 within the same image.
In fact one can choose to have as a reference point not only one of
the pixels at the edges of the CCD but also one or more pixels in the
center of the field, more distant from each other
than
the isokinetic angle.
within the same image.
In fact one can choose to have as a reference point not only one of
the pixels at the edges of the CCD but also one or more pixels in the
center of the field, more distant from each other
than
the isokinetic angle.
Finally, considering the observed tilt effect on the rigid movement of
the elongate LGS
to be of the same order of that introduced in Eq. (1)
one can recover (with the same equation but changing 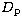 from the
diameter of the laser projector to the diameter of the seeing monitor)
the characteristic value of r0 for the night
during which the tests where performed.
from the
diameter of the laser projector to the diameter of the seeing monitor)
the characteristic value of r0 for the night
during which the tests where performed.


Up: Isokinetic patch measurements on
Copyright The European Southern Observatory (ESO)


![]() , with
, with ![]() ,and every frame containing s images
is reduceded to a matrix of s rows, each row corresponding to an edge.
Rows of the same matrix are scaled in order to have the same value
in the first element, that is equivalent to say:
,and every frame containing s images
is reduceded to a matrix of s rows, each row corresponding to an edge.
Rows of the same matrix are scaled in order to have the same value
in the first element, that is equivalent to say:

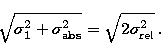
![]() , that is the value for
which the correlation decreases of a factor
, that is the value for
which the correlation decreases of a factor ![]() ,we fitted the data with the following function:
,we fitted the data with the following function:
![\begin{displaymath}
f(\theta) = \sqrt{2} \sigma_\theta \left[1-
\exp \left( -{\theta \over \theta_0 } \right) \right].\end{displaymath}](/articles/aas/full/1998/12/ds1440/img32.gif)
![]() within the same image.
In fact one can choose to have as a reference point not only one of
the pixels at the edges of the CCD but also one or more pixels in the
center of the field, more distant from each other
than
the isokinetic angle.
within the same image.
In fact one can choose to have as a reference point not only one of
the pixels at the edges of the CCD but also one or more pixels in the
center of the field, more distant from each other
than
the isokinetic angle.
![]() from the
diameter of the laser projector to the diameter of the seeing monitor)
the characteristic value of r0 for the night
during which the tests where performed.
from the
diameter of the laser projector to the diameter of the seeing monitor)
the characteristic value of r0 for the night
during which the tests where performed.