 |
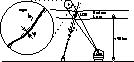
Figure 1: The effect of the atmospheric turbulence on the propagation of an LGS |
A Natural Guide Star (NGS) could be used as a further reference source to recover the absolute tilt of the LGS (Rigaut & Gendron 1992) but, from the scientific point of view, there is a major drawback due to the limited sky coverage, and for this reason it is not a useful technique.
Several other techniques have been proposed recently to recover the tilt of LGSs: (Foy et al. 1992; Foy et al. 1995; Belenk'ii 1994, 1995, 1996; Ragazzoni et al. 1995; Ragazzoni & Marchetti 1996; Ragazzoni 1996a,b, 1997). Some of these take advantage of the loss of reciprocity when the LGS is observed from a point of the earth's surface different from where it is projected.
Two different kinds of tilt perturbation, introduced into
the LGS path by the atmospheric turbulence, can be recognized when observing
the elongated projection in the sky of the laser.
The first one can be seen as a random and rigid motion
of the elongated LGS: it is a jittering effect due to the turbulence
met by the LGS in its way up to the sodium layer.
The other perturbation is a deviation ![]() from a straight propagation of the laser beacon (see Fig. 1).
The elongated LGS is corrugated by the atmospheric turbulence during its
propagation from the sodium layer to the observer;
in fact the laser stripe spans over a distance which is larger than the typical
coherence length of the atmospheric perturbations.
The light coming from different portions of the LGS is then affected
in different manners by the turbulence it has to go through:
the LGS is thus seen as a line of non coherent
sources (where "non coherent'' should be intended here as characterized
by non coherent movements)
and whose mutual distance is determined by the size of the isokinetic
patch.
from a straight propagation of the laser beacon (see Fig. 1).
The elongated LGS is corrugated by the atmospheric turbulence during its
propagation from the sodium layer to the observer;
in fact the laser stripe spans over a distance which is larger than the typical
coherence length of the atmospheric perturbations.
The light coming from different portions of the LGS is then affected
in different manners by the turbulence it has to go through:
the LGS is thus seen as a line of non coherent
sources (where "non coherent'' should be intended here as characterized
by non coherent movements)
and whose mutual distance is determined by the size of the isokinetic
patch.
Both tilt perturbations, either of the whole strip or of one single
part of the LGS within the same isokinetic patch,
are characterized by a Gaussian distribution around a mean
position, and a RMS, ![]() , given by:
, given by:
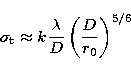 |
(1) |
From a theoretical point of view the size of the isokinetic patch
can be approximated with the following equation:
![\begin{displaymath}
\theta_0 \approx 0.3 {D \over \tilde h }\ [{\rm rad}],\end{displaymath}](/articles/aas/full/1998/12/ds1440/img7.gif) |
(2) |
Both perturbations are observed only perpendicularly to the projection in the sky of the laser (if it is a CW laser) and for this reason at least two elongated LGS are needed to recover a bidimensional perturbation.
As far as the isokinetic patch is concerned, the values one can find in the literature are based upon observations of small star clusters or speckle interferometry of double stars (McAlister 1976) and are summarized in Table 1.
The centroid motion of the stars is measured compared to a reference star and the information one can get about tilt are discretized in space, though continuous in time, because it is not possible to sample the atmospheric turbulence which is not passed through by the light of the stars. By the way, to our knoweledge, the only published attempt to estimate the isokinetic patch size from a continuous target, in this case the edge of the Sun, is by Kallistratova (1966). However, probably due to dominant ground layers occuring during daylight observations only a lower limit of 20'' is reported.
It is to be pointed out that knowing the size of the isokinetic
patch is very interesting for several reasons.
Considering the auxiliary telescopes technique
(Ragazzoni et al. 1995) for example, it is clear that the position
and the speed of the auxiliary telescopes depend upon
the size of the isokinetic patch around the NGS used to
overcome the tilt problem.
In fact the apparent position of the LGS must intersect both
the isokinetic patch of the target and of the NGS to
obtain the proper tilt of the target alone.
The isokinetic patch is a constraint also on the number of photons that
can be collected by the auxiliary telescope:
this is due to the fact that, of the whole elongated LGS, only
that portion which is within the same isokinetic patch is useful
to take differential tilt measurements.
As a consequence, also the power of the projected
laser and the diameter of the auxiliary
telescopes have to be established from the typical isokinetic
patch size at the observatory site.
In another tilt determination technique (Ragazzoni 1997) the same statements as above are true for the auxiliary projectors.
Finally one can consider two of the other proposed techniques (Belen'kii 1994; Ragazzoni 1995) in which increasing the field of view of the observer allows to consider more isokinetic patches at the same time. As a consequence, while the perturbation introduced during the upward path of the LGS remains the same, it is possible to separate with higher accuracy the contribution of the two perturbations to the tilt effect.
In this paper by imaging a portion of the edge of the Moon we describe the measurements of characteristical parameters of the atmospheric turbulence pretending to observe an elongated LGS.
Even though the edge of the Moon is not straight
(see Fig. 2) the curvature of the
surface has a negligible effect in the determination of
the correlation between the perturbations because
the interesting part of the observed portion
is less than 1 arcmin wide.
It can also be understood that the adopted
method of measuring the differential
perturbation between the edges of the Moon allows one to
ignore both the curvature and any feature of the lunar limb.
Copyright The European Southern Observatory (ESO)