

Up: Profiling of atmospheric turbulence
Subsections
It is now worthwhile to highlight a number of practical considerations with
respect to the actual implementation of the SCIDAR technique.
The theory outlined in Sect. 2.3 assumes an infinitely small spatial and
temporal scintillation detection sampling rate.
Obviously, however, for the practical implementation of SCIDAR one has to
compromise the level of detectable scintillation for the sake of obtaining a
reasonably high signal-to-noise level in the detected intensity.
Consequently our choice of spatial and temporal sampling means that the
level of scintillation detected will be less than that inferred by the
theory, leading to an underestimate of Cn2(h).
This may explain, for example, some of the relatively high values of
r0
we obtain - as shown in Sect. 4.
For the relatively low sampling rates used in our system
(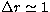 cm pix-1 and
cm pix-1 and 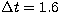 or 2.7 ms) this
underestimate
could be corrected, to first order, by linearly-calibrating our results with
respect to the integrated Cn2(h) value determined by other means during the
observations. This feasibility is planned for our purpose-built SCIDAR system
currently under construction.
At any particular time during an observation run a number of
binary star objects may be available for the collection of SCIDAR data.
Therefore an obvious consideration one first has to make is regarding the
signal-to-noise trade-off between various potential targets.
Given the magnitudes of each component for a number of potential targets,
one can calculate the error propagation for the expression involving
B1 and B1 in the second term of Eq. (10) to predict the relative
average signal-to-noise ratio (SNR) with respect to photon noise.
or 2.7 ms) this
underestimate
could be corrected, to first order, by linearly-calibrating our results with
respect to the integrated Cn2(h) value determined by other means during the
observations. This feasibility is planned for our purpose-built SCIDAR system
currently under construction.
At any particular time during an observation run a number of
binary star objects may be available for the collection of SCIDAR data.
Therefore an obvious consideration one first has to make is regarding the
signal-to-noise trade-off between various potential targets.
Given the magnitudes of each component for a number of potential targets,
one can calculate the error propagation for the expression involving
B1 and B1 in the second term of Eq. (10) to predict the relative
average signal-to-noise ratio (SNR) with respect to photon noise.
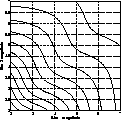 |
Figure 7:
Contour plot of the relative SNR for various binary star magnitude
combinations. Contours are at 10% the peak level. The values decrease from left
to right |
Figure 7 shows such a calculation for a typical range of values
encountered
in practice and enables one therefore to make an informed choice.
However, if one is collecting data across the whole telescope pupil
using a telescope with a large obstruction ratio, one also has to take into
account the effect of the pupil transfer function upon the SNR within
the correlation plane. This is particularly so if one is operating in the
generalised
SCIDAR mode since one is then imaging the scintillation pattern viewed through
two overlapping pupils. The degree of pupil overlap is directly proportional to
both the angular separation of the binary and the effective distance below
the telescope pupil one defocuses to.
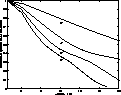 |
Figure 8:
Example transfer functions of overlapping pupils, for the generalised
SCIDAR case, as a function of altitude. Curves are given for binary star
separations of 2, 4, 6 & 8 arcseconds and assume a telescope diameter of 1 m and
1 cm pix-1 image plane sampling |
Figure 8 shows the predicted pupil overlap transfer function
for various binary separations assuming a 1 m telescope pupil of
obstruction ratio 0.3 and a typical defocus distance of 3.5 km. As can be
seen in the most extreme case, for example beyond separations of 8
arcseconds, the distorted transfer function can significantly reduce the
SNR for high altitudes.
Since close to zenith, 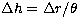 , in theory one is
free to choose whatever
altitude sampling length is required. However, for a particular telescope
diameter D, in practice a restriction is imposed by the requirement that the
maximum height attained should be greater than the sum of the height for
which optical turbulence is assumed to be negligible and the magnitude of
the generalised SCIDAR conjugate plane distance,
, in theory one is
free to choose whatever
altitude sampling length is required. However, for a particular telescope
diameter D, in practice a restriction is imposed by the requirement that the
maximum height attained should be greater than the sum of the height for
which optical turbulence is assumed to be negligible and the magnitude of
the generalised SCIDAR conjugate plane distance, 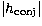 ,
ie:
,
ie: 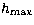 = D/
= D/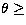 20 km +
20 km + 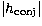 .
.
These restrictions upon binary star separation are shown graphically
in Fig. 9 for an assumed pupil sampling of 1 cm pix-1, a
telescope pupil diameter
of 1 m and a conjugate plane distance of 3.5 km.
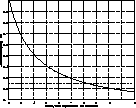 |
Figure 9:
Plot of altitude resolution as a function of binary separation showing
the limits imposed for a reasonable altitude sampling (top) and a maximum
altitude reached of 25 km above image plane (bottom), for a 1 m telescope assuming
1 cm pix-1 image plane sampling |
Taken in combination, the restrictions implied in Fig. 8 and
Fig. 9 show that for this
particular configuration, binary separations between around 4-7
arcseconds are desirable.
It must be noted that both the upper limit upon 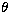 and the
SNR within the correlation plane can be increased, if using a
telescope of a large enough diameter (e.g. D > 3.5 m) to enable an
artificial circular pupil greater than 1m to be imposed within the image of
the segment of the mirror observed.
In this case, assuming a similar pupil sampling as previously, the
restriction upon
and the
SNR within the correlation plane can be increased, if using a
telescope of a large enough diameter (e.g. D > 3.5 m) to enable an
artificial circular pupil greater than 1m to be imposed within the image of
the segment of the mirror observed.
In this case, assuming a similar pupil sampling as previously, the
restriction upon 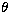 then only originates from the size of the CCD,
such that in our case
then only originates from the size of the CCD,
such that in our case 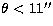 .
.
Having calculated a solution Cn2(h) profile from the data,
one also requires some knowledge of the reliability of this solution.
Although this is difficult to ascertain directly when using the iterative
maximum
entropy routine (Sect. 2) due to the non-linear nature of the iterative
procedure,
it has been found that it is possible to estimate the RMS error of a solution
using a numerical approach.
To enable this we define a ``solution plane", which contains both the true
(and unknown) 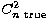 profile and the best-fit solution
profile,
profile and the best-fit solution
profile,  , and a ``data plane", within which
resides both the true (observed) data,
, and a ``data plane", within which
resides both the true (observed) data, 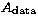 , and the correlation
function obtained from the
, and the correlation
function obtained from the  profile,
profile,
 .
.
A schematic outline of this representation is shown in Fig. 10.
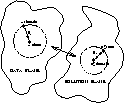 |
Figure 10:
Schematic description of the method used to estimate the RMS error on
any particular Cn2(h) profile obtained |
Given that one can then represent the RMS difference 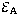 given by Eq. (15), as the geometrical distance in the data plane between
given by Eq. (15), as the geometrical distance in the data plane between
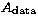 and the final
and the final  , what one wishes to find is
the corresponding distance between
, what one wishes to find is
the corresponding distance between 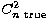 and
and
 , namely
, namely 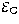 - as
indicated in Fig. 10.
- as
indicated in Fig. 10.
The approach taken here is to numerically perturb the
 profile
about its position within the solution plane by incremental distances by
applying random Gaussian noise, until the RMS distance within the data plane
between its
corresponding correlation function and
profile
about its position within the solution plane by incremental distances by
applying random Gaussian noise, until the RMS distance within the data plane
between its
corresponding correlation function and 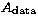 is equal to the RMS
distance
is equal to the RMS
distance 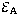 .
When this occurs the RMS distance between
.
When this occurs the RMS distance between
 and its perturbed value can then be considered as
describing
the radius of a circle within the solution plane upon which the ``true" value of
Cn2(h) lies and therefore represents a reasonable
approximation of the RMS error
and its perturbed value can then be considered as
describing
the radius of a circle within the solution plane upon which the ``true" value of
Cn2(h) lies and therefore represents a reasonable
approximation of the RMS error 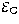 .
.
In doing so one is assuming that the solution  is
close to the
global minimum within the solution plane, or at least within a local minimum
which
is not very different from the true solution.
This assumption is justified both by the relatively low
value of
is
close to the
global minimum within the solution plane, or at least within a local minimum
which
is not very different from the true solution.
This assumption is justified both by the relatively low
value of 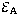 we achieve prior to termination of the iterative
routine and also by the strongly linear relationship that has been found
in all cases between
we achieve prior to termination of the iterative
routine and also by the strongly linear relationship that has been found
in all cases between
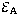 and
and 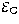 as the degree of perturbation
applied to
as the degree of perturbation
applied to  is increased.
is increased.
Having performed this calculation for a number of different Cn2(h)
profiles, it has been found that the value of 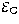 is greater
than the value
of
is greater
than the value
of 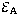 in most cases.
For example for the case shown in Fig. 5,
in most cases.
For example for the case shown in Fig. 5, 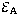 and
and
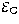 are
found to be 4.3% and 7.2% respectively.
This highlights the need for high SNR data for a reliable Cn2(h)
solution.
are
found to be 4.3% and 7.2% respectively.
This highlights the need for high SNR data for a reliable Cn2(h)
solution.


Up: Profiling of atmospheric turbulence
Copyright The European Southern Observatory (ESO)


![]() and the
SNR within the correlation plane can be increased, if using a
telescope of a large enough diameter (e.g. D > 3.5 m) to enable an
artificial circular pupil greater than 1m to be imposed within the image of
the segment of the mirror observed.
In this case, assuming a similar pupil sampling as previously, the
restriction upon
and the
SNR within the correlation plane can be increased, if using a
telescope of a large enough diameter (e.g. D > 3.5 m) to enable an
artificial circular pupil greater than 1m to be imposed within the image of
the segment of the mirror observed.
In this case, assuming a similar pupil sampling as previously, the
restriction upon ![]() then only originates from the size of the CCD,
such that in our case
then only originates from the size of the CCD,
such that in our case ![]() .
.![]() profile and the best-fit solution
profile,
profile and the best-fit solution
profile, ![]() , and a ``data plane", within which
resides both the true (observed) data,
, and a ``data plane", within which
resides both the true (observed) data, ![]() , and the correlation
function obtained from the
, and the correlation
function obtained from the ![]() profile,
profile,
![]() .
.

![]() profile
about its position within the solution plane by incremental distances by
applying random Gaussian noise, until the RMS distance within the data plane
between its
corresponding correlation function and
profile
about its position within the solution plane by incremental distances by
applying random Gaussian noise, until the RMS distance within the data plane
between its
corresponding correlation function and ![]() is equal to the RMS
distance
is equal to the RMS
distance ![]() .
When this occurs the RMS distance between
.
When this occurs the RMS distance between
![]() and its perturbed value can then be considered as
describing
the radius of a circle within the solution plane upon which the ``true" value of
Cn2(h) lies and therefore represents a reasonable
approximation of the RMS error
and its perturbed value can then be considered as
describing
the radius of a circle within the solution plane upon which the ``true" value of
Cn2(h) lies and therefore represents a reasonable
approximation of the RMS error ![]() .
.![]() is
close to the
global minimum within the solution plane, or at least within a local minimum
which
is not very different from the true solution.
This assumption is justified both by the relatively low
value of
is
close to the
global minimum within the solution plane, or at least within a local minimum
which
is not very different from the true solution.
This assumption is justified both by the relatively low
value of ![]() we achieve prior to termination of the iterative
routine and also by the strongly linear relationship that has been found
in all cases between
we achieve prior to termination of the iterative
routine and also by the strongly linear relationship that has been found
in all cases between
![]() and
and ![]() as the degree of perturbation
applied to
as the degree of perturbation
applied to ![]() is increased.
is increased.
![]() is greater
than the value
of
is greater
than the value
of ![]() in most cases.
For example for the case shown in Fig. 5,
in most cases.
For example for the case shown in Fig. 5, ![]() and
and
![]() are
found to be 4.3% and 7.2% respectively.
This highlights the need for high SNR data for a reliable Cn2(h)
solution.
are
found to be 4.3% and 7.2% respectively.
This highlights the need for high SNR data for a reliable Cn2(h)
solution.