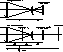
Figure 2:
Schematic diagram of the optical system for SCIDAR. a) shows
the optical system for pupil plane SCIDAR. In this mode the telescope
entrance pupil is imaged by the telescope mirror system L1 and the field
lens L2. The focal length of the lens L2 is chosen to give the
correct image size at the detector plane. The image is effectively at
infinity so that the final pupil image is formed at approximately the focal
distance f2 behind L2. b) shows the optical system for
generalised SCIDAR. At the CCD plane this system forms a pupil image from a
plane located the required distance behind the telescope mirror (![]() ).
For this case then, the telescope mirrors (L1) form a virtual image of
the plane of focus (P1) at a distance
).
For this case then, the telescope mirrors (L1) form a virtual image of
the plane of focus (P1) at a distance ![]() behind the telescope
mirror. The new field lens L'2 re-images this virtual object to form the
pupil image at the CCD plane. For example, for the JKT at La Palma; the
telescope has a 1 m pupil with a F/15 focal ratio. A 159 mm field lens
L2 is required to give the correct image size for pupil plane SCIDAR. For
Generalised SCIDAR the field lens L2 is replaced by a lens with a focal
length of 46 mm (L'2), still located at 159 mm from the CCD plane. A
virtual image of a plane at 3.5 km is formed
behind the telescope
mirror. The new field lens L'2 re-images this virtual object to form the
pupil image at the CCD plane. For example, for the JKT at La Palma; the
telescope has a 1 m pupil with a F/15 focal ratio. A 159 mm field lens
L2 is required to give the correct image size for pupil plane SCIDAR. For
Generalised SCIDAR the field lens L2 is replaced by a lens with a focal
length of 46 mm (L'2), still located at 159 mm from the CCD plane. A
virtual image of a plane at 3.5 km is formed ![]()
![]() 64 mm in
front of L'2 and this virtual object is imaged by L'2 onto the CCD
detector
64 mm in
front of L'2 and this virtual object is imaged by L'2 onto the CCD
detector
Figure 1 shows that in a simplified one-dimensional
representation of the observing procedure for a binary object observed
at zenith (a), a peak in the correlation plane occurs at a pupil
separation ![]() , (b), and thus by
simple geometry, denotes the presence of a single turbulent layer
at an altitude
, (b), and thus by
simple geometry, denotes the presence of a single turbulent layer
at an altitude ![]() above the telescope pupil.
This simple situation can be generalised to the case where multiple turbulent
layers exist, each one having an associated altitude calculable from the peak
position within the average correlation.
Also for the general case where the binary star is observed at some
zenith angle z, then the geometrical conversion above becomes
above the telescope pupil.
This simple situation can be generalised to the case where multiple turbulent
layers exist, each one having an associated altitude calculable from the peak
position within the average correlation.
Also for the general case where the binary star is observed at some
zenith angle z, then the geometrical conversion above becomes ![]() .
.
In the conventional operation of SCIDAR, the conjugate plane of the imaging system is placed at the altitude of the pupil of the telescope - referred to here as pupil-plane SCIDAR. However, low altitude turbulence cannot be determined in this mode since the scintillation requires a large distance over which to develop a signal strong enough to be detected. Consequently the correlation signal close to zero altitude is occupied only by a central core corresponding to the sum of all other higher altitude peaks. This is shown diagrammatically as the central peak in Fig. 1a. Recently, however, a solution to this problem was proposed by Fuchs et al. (1994) in which one changes the conjugate height of the imaging system from that of the telescope pupil, to one some distance below it. In effect, this creates an extra distance for the scintillation pattern to develop to a detectable level and also shifts the central core to below the pupil (zero) altitude. Experiments performed by us in this generalised SCIDAR mode appear to confirm the validity of this approach and the results are discussed later in Sect. 4.
 |
Figure 3: Example average scintillation pattern image obtained in the generalised SCIDAR mode at the JKT, in La Palma from 18000 1.6 ms exposure frames. The scale is in relative intensity units |
For example, for the Jacobus Kapteyn Telescope (JKT) in La Palma, the telescope has a 1m pupil with an F/15 focal ratio and therefore an ideal focal length for the field lens (L2), to give this required sampling, would be 159 mm. This would produce a 10.6 mm diameter pupil image at the intensifier, or equivalently a 2.04 mm pupil image on the CCD.
For the generalised mode shown in Fig. 2b, the field lens (L2) is replaced by one of a different focal length, L'2. The separation of field lens position to intensifier is unchanged however and thus the pupil plane sampling remains unchanged also. Using the thin lens equation one can calculate the required focal length for this generalised field lens for any chosen height of generalisation. For our measurements we are primarily concerned with ascertaining the strength and velocity of all turbulence present above the telescope altitude by conjugating to altitudes below that of the telescope pupil. Therefore for example, again for the JKT, in order to conjugate to a distance of 3.5 km, say, then a field lens of 46mm focal length is required.
The digital output from the DALSA Camera is acquired by a Bitflow Raptor PCI frame capture board controlled by a fast PC and the data is stored directly onto Digital Linear Tape. The frame exposure times normally used are 1.6 ms and 2.7 ms, with frame acquisition rates of 305 and 188 frames per second respectively.
Figure 3 shows an example of the average scintillation pattern of 18000 frames obtained using this system on the JKT whilst running in the generalised SCIDAR mode. The sheared image of the telescope pupil is clearly visible.
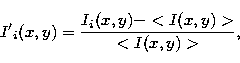 |
(9) |
The finite width of these peaks results directly
from the Fresnel length associated with each turbulent layer, given
by ![]() (Vernin & Azouit
1983).
This in turn effectively limits the degree of resolution in Cn2(h)
attainable from the SCIDAR data.
For the data collected thus far,
(Vernin & Azouit
1983).
This in turn effectively limits the degree of resolution in Cn2(h)
attainable from the SCIDAR data.
For the data collected thus far, ![]() ranges from
around 700 m (for a pupil-conjugate distance of say 3 km) to around 2000 m
(for the maximum altitudes considered).
Assuming a pupil plane sampling,
ranges from
around 700 m (for a pupil-conjugate distance of say 3 km) to around 2000 m
(for the maximum altitudes considered).
Assuming a pupil plane sampling, ![]() , of 1 cm pix-1 and
binary star separations between 4-9'', then
the altitude sampling available, given by
, of 1 cm pix-1 and
binary star separations between 4-9'', then
the altitude sampling available, given by
![]() ,
corresponds to around 200-500 m, and thus represents a reasonable sampling
rate of the Fresnel length at all altitudes.
,
corresponds to around 200-500 m, and thus represents a reasonable sampling
rate of the Fresnel length at all altitudes.
A slice taken through the correlation plane, parallel to the direction of
the binary star, ![]() , can then be expressed as (Vernin &
Roddier 1975),
, can then be expressed as (Vernin &
Roddier 1975),
![\begin{eqnarray}
C_{\rm I}(r,\theta) & = & \left( \frac{B_{1}^{2} +
B_{2}^{2}}{(...
...B_{2})^{2}} \right)[
A_{\rm I}(r,\theta) + A_{\rm I}(r,-\theta) ]\end{eqnarray}](/articles/aas/full/1998/10/ds7086/img39.gif) |
||
| (10) |
The log amplitude covariance of the scintillation fluctuations then follows as,
![\begin{displaymath}
A_{\chi}(r,\theta) = \frac{ \ln [A_{\rm I}(r,\theta) + 1]}{4}, \end{displaymath}](/articles/aas/full/1998/10/ds7086/img42.gif) |
(11) |
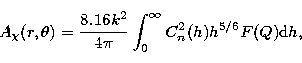 |
(12) |
![\begin{displaymath}
F(Q) = \int_{0}^{\infty}{ K^{-8/3} J_{0}(QK) [1 - \cos(K^2)] {\rm d}K }, \end{displaymath}](/articles/aas/full/1998/10/ds7086/img46.gif) |
(13) |
![\begin{displaymath}
Q = \left[ \frac{k}{h {\rm sec}(z)} \right]^{1/2} \mid r - \theta h
{\rm sec}(z) \mid. \vspace{0.5cm}\end{displaymath}](/articles/aas/full/1998/10/ds7086/img47.gif) |
(14) |
The particular method one might employ for this problem (and also to
some extent the confidence of the solution) depends very much upon the
Cn2(h) altitude sampling that is required.
Tests performed upon a number of high resolution Cn2(h) profiles
obtained by balloon-borne instruments (Vernin & Muñoz-Tuñôn
1992)
have shown that the main parameters
which determine AO anisoplanatic performance can be calculated with reasonable
accuracy provided that the altitude sampling, ![]() , is less than 1km.
For the data collected thus far, the altitude resolution available is between
around 200-500 m, and
therefore comfortably within this constraint.
However it has been found that a simple least-squares inversion of Eq. (12)
for these data is incapable of producing a reliable solution unless one
rectangularises the two-dimensional integral equation such that multiple pupil
samples
map onto each altitude sample and
, is less than 1km.
For the data collected thus far, the altitude resolution available is between
around 200-500 m, and
therefore comfortably within this constraint.
However it has been found that a simple least-squares inversion of Eq. (12)
for these data is incapable of producing a reliable solution unless one
rectangularises the two-dimensional integral equation such that multiple pupil
samples
map onto each altitude sample and ![]() remains fixed at
1 cm pix-1 but
remains fixed at
1 cm pix-1 but ![]() is extended to 2-3 km.
is extended to 2-3 km.
Although, ultimately, it is the Fresnel length that limits the altitude
resolution attainable, in an effort to realise the altitude sampling that is
made available
by that within the pupil, a number of iterative inversion methods have been
explored.
One that has proved successful is based upon a maximum entropy routine
which also allows for the controlled propagation of noise between the data and
solution
(Skilling & Bryan 1984).
In practice, we first calculate a crude (large ![]() )
least-squares inversion of Cn2(h) using a rectangularised version
of Eq. (12) and then use an interpolated version of this as the first guess
estimate for the iterative routine.
As an aid to deciding when the routine should be terminated, the following
RMS difference error metric is calculated following each iteration:
)
least-squares inversion of Cn2(h) using a rectangularised version
of Eq. (12) and then use an interpolated version of this as the first guess
estimate for the iterative routine.
As an aid to deciding when the routine should be terminated, the following
RMS difference error metric is calculated following each iteration:
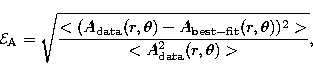 |
(15) |
In Fig. 5, (a) shows the correctly scaled correlation slice,
![]() , of Fig. 4a, and in (b) the corresponding
Cn2(h)
profile obtained.
Also shown in Fig. 5a, for comparison is
, of Fig. 4a, and in (b) the corresponding
Cn2(h)
profile obtained.
Also shown in Fig. 5a, for comparison is
![]() which gives some indication of the accuracy of
the solution obtained where, in this case,
which gives some indication of the accuracy of
the solution obtained where, in this case, ![]() .
It is interesting to note that for the particular example shown here the
apparent
single correlation peak at a height of 7.5 km in Fig. 5a has
been resolved into two distinct turbulent layers within the corresponding
Cn2(h) profile of Fig. 5b at heights of 7.2 km and 8.1 km.
.
It is interesting to note that for the particular example shown here the
apparent
single correlation peak at a height of 7.5 km in Fig. 5a has
been resolved into two distinct turbulent layers within the corresponding
Cn2(h) profile of Fig. 5b at heights of 7.2 km and 8.1 km.
The apparent width of the dominant turbulent layers shown here probably does not reflect the true physical depth over which the optical turbulence exists. It is more likely that this apparent spread of Cn2(h) values is due to the effective resolution imposed by the Fresnel length, as discussed in Sect. 2.3.1. Therefore, although it appears that one is oversampling each peak in the Cn2(h) profile, the suspicion is that in fact the layers of turbulence themselves could be substantially thinner.
Confidence in the inversion methods used has been obtained by testing them on realistic simulated SCIDAR data generated using a Fresnel wavefront propagation code developed within our group (Adcock et al. 1996).
 |
Figure 6: a) Simulated spatial correlation data along with b) a comparison of the model input Cn2(h) profile (bar-plot) and that obtained using our integral inversion method |
Figure 4b shows such a plot generated from the same data as in
Fig. 4a,
with ![]() = 23 ms (corresponding to
= 23 ms (corresponding to ![]() =0.42 ms-1).
The zero velocity position within this plot is denoted at the centre by a
cross.
In comparing this with the spatial-correlation plot of Fig. 4a one
can see that, as indicated by the the Cn2(h) of Fig. 5b, the
apparent
single peak at the greatest distance from the central core has been resolved
into two layers at heights of 7.2 km and 8.1 km with associated velocities
of 14.6 ms-1 (wind direction Position Angle, PA = 103
=0.42 ms-1).
The zero velocity position within this plot is denoted at the centre by a
cross.
In comparing this with the spatial-correlation plot of Fig. 4a one
can see that, as indicated by the the Cn2(h) of Fig. 5b, the
apparent
single peak at the greatest distance from the central core has been resolved
into two layers at heights of 7.2 km and 8.1 km with associated velocities
of 14.6 ms-1 (wind direction Position Angle, PA = 103![]() ) and
9.8 ms-1 (PA = 130
) and
9.8 ms-1 (PA = 130![]() ) respectively.
It is also worth noting that the correlation peak closest to the central core
(corresponding to a height close to the telescope pupil) has shifted only very
slightly from its central position in the spatial-correlation (V =
0.01 ms- 1).
This is indicative perhaps of the presence of almost static turbulence within
the telescope dome since the ground wind speed recorded at this time was
13 ms-1.
) respectively.
It is also worth noting that the correlation peak closest to the central core
(corresponding to a height close to the telescope pupil) has shifted only very
slightly from its central position in the spatial-correlation (V =
0.01 ms- 1).
This is indicative perhaps of the presence of almost static turbulence within
the telescope dome since the ground wind speed recorded at this time was
13 ms-1.
The algorithm to allow automative calculation of V(h) is based upon the assumption that the optical turbulence is highly discretised (the justification for this is clarified later in Sect. 4). Having first determined the altitudes of each discrete layer and the orientation of the binary star observed, a template is then constructed for each layer, each one representing their individual spatial correlation signal. The cross-correlation of each of these templates with the spatio-temporal plot then allows the speed and direction of each layer to be identified.
Copyright The European Southern Observatory (ESO)