

Up: Profiling of atmospheric turbulence
The method described in this paper for remote turbulence profiling
is based upon the SCIntillation Detection And Ranging (SCIDAR)
technique which relies upon the analysis of crossed beam (i.e. binary
star) scintillation patterns.
This technique has been developed by Vernin and co-workers over a
number of years
(Vernin & Roddier 1973;
Rocca et al. 1974;
Vernin & Roddier 1975;
Roddier & Vernin 1977;
Azouit et al. 1978;
Vernin et al. 1979;
Azouit & Vernin 1980;
Vernin & Azouit 1983;
Vernin et al. 1991)
and more recently by Tyler (1992).
A number of specific site investigations have been attempted using
either SCIDAR alone (e.g. Racine & Ellerbroek 1995) or
in combination with
temperature and
pressure data obtained using balloon-borne instrumentation
(Vernin et al. 1990;
Vernin & Muñoz-Tuñôn 1992,
1994). A number of spatial filtering techniques
applied to scintillation signal detection from single stars have also been
proposed for this particular problem (e.g. Ochs et al.
1976; Churnside et al. 1988;
Zavorotny 1992).
However, although the performance of SCIDAR is constrained by the
availability of suitable binary star objects, one is able to obtain reliable
profiles of a finer altitude sampling than that possible using spatial filtering
methods on single stars.
With SCIDAR the strength of scintillation is used to estimate both the
value of the atmospheric optical turbulence profile, Cn2(h), and the
turbulence velocity, V(h), as a function of height, h, using a
triangulation technique. The methodology used here involves recording a
large number of instantaneous scintillation patterns from a double star,
calculating the average spatial and temporal correlation, and extracting the
Cn2(h) profile using an integral inversion method and the V(h) profile
using template correlation.
Until very recently it was expected that such a method would be
unable to characterise low altitude (< 5 km) turbulence, thus requiring
other techniques to be used in unison with SCIDAR to complete the
profile information. However, as discussed later, the introduction of
the concept of generalised SCIDAR by Fuchs et al.
(1994), has shown that
a simple modification of the basic SCIDAR method can allow this
information to be recovered without this requirement, and here we show
example results from our generalised SCIDAR experiments at various
observing sites.
Although the profiling of optical turbulence and velocity is of great
intrinsic interest in terms of atmospheric science, the main impetus
for these experiments has been to obtain real Cn2(h) and V(h)
data for our theoretical work in the study of adaptive optics (AO)
systems for astronomy.
The main concern of optimising traditional astronomical observations
at a particular observing site has been with respect to the angular
extent of the seeing disc observed at ground level, 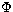 ,
which can be expressed simply as,
,
which can be expressed simply as,
| 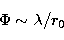 |
(1) |
where r0 is the turbulence coherence length given by,
| ![\begin{displaymath}
r_{0} = \left[ 0.42 k^2 \cos^{-1}(z) \int C_n^2(h) {\rm d}h \right]^{-3/5}, \end{displaymath}](/articles/aas/full/1998/10/ds7086/img3.gif) |
(2) |
k is the wavenumber and z is the zenith angle of observation.
Since 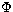 can be measured directly using long exposure imaging or
indirectly using differential image motion (DIMM) methods (Martin
1987),
explicit
knowledge of the Cn2(h) profile itself is unnecessary for this
purpose.
However, in the design of an AO system for a particular astronomical
observing site, not only does one require some
knowledge of the statistics of the size of the seeing disc, but also
that of the turbulence and velocity profile with height so that
one may have some expectation of the detrimental effects of
anisoplanatism.
For example, for Angular Anisoplanatism (AA), the decorrelation with angle
can be measured directly using long exposure imaging or
indirectly using differential image motion (DIMM) methods (Martin
1987),
explicit
knowledge of the Cn2(h) profile itself is unnecessary for this
purpose.
However, in the design of an AO system for a particular astronomical
observing site, not only does one require some
knowledge of the statistics of the size of the seeing disc, but also
that of the turbulence and velocity profile with height so that
one may have some expectation of the detrimental effects of
anisoplanatism.
For example, for Angular Anisoplanatism (AA), the decorrelation with angle
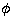 between the science object wavefront and the measured wavefront
can be quantified in terms of the mean squared error between the two
wavefronts, such that
between the science object wavefront and the measured wavefront
can be quantified in terms of the mean squared error between the two
wavefronts, such that
| 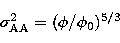 |
(3) |
where 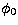 , the isoplanatic angle, is given by,
, the isoplanatic angle, is given by,
| ![\begin{displaymath}
\phi_{0} = \left[ 2.9 k^2 \cos^{-1}(z) \int C_n^2(h) {h}^{5/3} {\rm d}h
\right]^{- 3/5}. \end{displaymath}](/articles/aas/full/1998/10/ds7086/img7.gif) |
(4) |
Similarly, for an AO system guided by an artificially produced laser
beacon, the decorrelation between the science object wavefront and
the wavefront sampled by the beacon which leads to Focal Anisoplanatism (FA),
can also be quantified in terms of Cn2(h) such that the mean
squared error between the two wavefronts is given by,
| 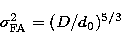 |
(5) |
where D is the telescope diameter and d0 can be interpreted as an
measure of the effective diameter of the AO imaging system when a single
laser beacon is being used and can be approximated as,
| ![\begin{displaymath}
d_{0} \simeq
\left[ k^2 \cos^{-1}(z) \int_{0}^{H} C_n^2(h) {(h/H)}^{5/3} {\rm d}h
\right]^{- 3/5},\end{displaymath}](/articles/aas/full/1998/10/ds7086/img9.gif) |
(6) |
where H is the laser beacon altitude.
Knowledge of the velocity profile of the turbulent layers
becomes useful when one considers the effect of Temporal
Anisoplanatism (TA) in the AO corrected image due to the finite dwell time
of the system between measuring the guide star wavefront and
correcting the science object wavefront, 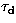 .
Once again, this can be quantified in terms of the mean
squared error between the two wavefronts such that,
.
Once again, this can be quantified in terms of the mean
squared error between the two wavefronts such that,
| 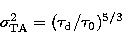 |
(7) |
where  is given in terms of both V(h) and Cn2(h) as,
is given in terms of both V(h) and Cn2(h) as,
| ![\begin{displaymath}
\tau_{0} = \left[ 2.9 k^2 \int C_n^2(h) {V(h)}^{5/3} {\rm d}h
\right]^{-3/5}.\end{displaymath}](/articles/aas/full/1998/10/ds7086/img13.gif) |
(8) |
Consequently if one has knowledge of both Cn2(h) and V(h), then
all of the parameters which describe the performance of an AO system
can be obtained.
In the future one could also envisage a real-time SCIDAR system
being available to allow anisoplanatic effects to be
quantified during an AO observing run, thus enabling image quality diagnostics
to be made and provide information for reliable point spread function
deconvolution if deemed necessary.


Up: Profiling of atmospheric turbulence
Copyright The European Southern Observatory (ESO)
![]() ,
which can be expressed simply as,
,
which can be expressed simply as,
![\begin{displaymath}
r_{0} = \left[ 0.42 k^2 \cos^{-1}(z) \int C_n^2(h) {\rm d}h \right]^{-3/5}, \end{displaymath}](/articles/aas/full/1998/10/ds7086/img3.gif)
![\begin{displaymath}
\phi_{0} = \left[ 2.9 k^2 \cos^{-1}(z) \int C_n^2(h) {h}^{5/3} {\rm d}h
\right]^{- 3/5}. \end{displaymath}](/articles/aas/full/1998/10/ds7086/img7.gif)
![\begin{displaymath}
d_{0} \simeq
\left[ k^2 \cos^{-1}(z) \int_{0}^{H} C_n^2(h) {(h/H)}^{5/3} {\rm d}h
\right]^{- 3/5},\end{displaymath}](/articles/aas/full/1998/10/ds7086/img9.gif)
![]() .
Once again, this can be quantified in terms of the mean
squared error between the two wavefronts such that,
.
Once again, this can be quantified in terms of the mean
squared error between the two wavefronts such that,
![\begin{displaymath}
\tau_{0} = \left[ 2.9 k^2 \int C_n^2(h) {V(h)}^{5/3} {\rm d}h
\right]^{-3/5}.\end{displaymath}](/articles/aas/full/1998/10/ds7086/img13.gif)