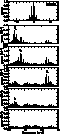
Figure 4: Power spectra of V 465 Per observed between November, 1994 and January, 1995. The spectral window is shown in the top panel. Four frequencies can be identified in the next four panels
It is somewhat difficult to resolve multiple pulsation frequencies from complicated light curves. Particularly, prewhitening procedure extracting step by step each real frequency in the power spectrum should be done carefully. We performed the frequency analysis using a package of computer programs, which utilize DFT (Discrete Fourier Transform) and multiple linear least square fitting method. The sinusoidal variation corresponding to the previously identified frequencies is subtracted from the original time-domain data, similar to PERIOD program used by the Breger group (for example, Breger et al. 1994) and the sequential CLEANest algorithm (Foster 1995). The detailed prewhitening methods and period searching techniques were given in Paper II.

Figure 4: Power spectra of V 465
Per observed between November, 1994 and January, 1995.
The spectral window is shown in the top panel.
Four frequencies can be identified
in the next four panels
The power spectra of V 465 Per are shown in Fig. 4 (click here). The spectral window in the first panel shows strong side bands, particularly at 1 cycle/day which is produced by the daily gaps of observation. After the successive prewhitening of each frequency peak, four frequencies are identified in the next four panels as follows; f1=14.040 c/d, f2=17.208 c/d, f3=33.259 c/d, f4=13.721 c/d. The observational results of V 465 Per are summarized in Table 1 (click here). The fourth frequency which has a smaller value of signal to noise amplitude ratio (S/N) than the criterion of 4.0 (Breger et al. 1993) might be uncertain. In the last panel, the power spectrum of the data after subtraction of four frequencies shows some additional peaks, probably caused by the observation noise.
Slovak (1978) detected two pulsation period of V 465 Per. A period of 1.92 hours (= 12.50 c/d) was shown in his light curves obtained from two nights of observations and the secondary period of 43 minutes (= 33.49 c/d) was detected using a frequency analysis. The first frequency having the most dominant pulsation amplitude may correspond to our f1 and the second frequency is similar to our f3. The other two frequencies (f2 and f4) detected in this study might not be found in his result due to his limited data sets.
|
This study (Nov. 1994 | Slovak (1978) | ||||||
| Frequency | Q ( | | | | Frequency | ||
| f1=14.040 c/d | 162.5 | | | 11.8 | -0.14 | 12.50 c/d | |
| f2=17.208 | 199.2 | 4.25 | 2.3 | 7.8 | +2.05 | -- | |
| f3=33.259 | 384.9 | 2.20 | 1.7 | 6.1 | +1.93 | 33.49 | |
| f4=13.721 | 158.8 | 5.33 | 1.1 | 3.9 | +3.55 | -- | |
| Residuals | 4.14 mmag | ||||||
|
| |||||||
![]() :
: ![]()
![]() : S/N =
(power for each frequency/mean power in the range of
: S/N =
(power for each frequency/mean power in the range of ![]() c/d after prewhitening of all frequencies)1/2.
c/d after prewhitening of all frequencies)1/2.