The first goal of the star tracker is to provide image stabilization for better measurement of
astrophysical quantities. But correction of atmospheric fluctuations also yields information about
turbulence. The Fried parameter r0 can be estimated from the angle of arrival variance according to Eq.
(12) In this paper, r0 values are given at 600 nm, the mean wavelength of the star tracker system.
The atmospheric perturbation can be measured either in open loop from the quad cell signal, or in
closed loop from the mirror position. In both cases, these data include mechanical vibrations inside the
instrument and telescope drift, and cannot therefore provide accurate r0 measurement, but rather
qualitative estimation of the strength of the turbulence to be corrected. Since the correction is not
perfect, mirror position reflects the atmospheric angle of arrival filtered by the closed loop transfer
function, whose cutoff frequency is close to the atmospheric one (63 Hz in comparison with 11.5 Hz),
see Figs. 5 (click here) and 8 (click here). Deconvolution with the servo transfer function would therefore be interesting for a
better estimate, but not implemented for the results of this paper. This closed loop mode is used for a
posteriori r0 calculation (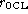
),
from files of mirror position in which the (assumedly linear) telescope
drift was subtracted.
Since the sampling frequency of the quad cell is much higher (165 Hz in open loop), a real-time r0
estimation (
) can be made from the quad cell data in open loop mode. The drawback in this case is
that the linear area of the quad cell roughly equals the size of the focal spot: the star must be centered
and only small angles of arrival can be directly measured. Nevertheless, this mode has been
implemented on ASSI, with a very low frequency correction to keep the spot centered. We assume that
the correction is performed in the linear area of the quad-cell. The quad-cell calibration is automatically
performed before data acquisition and is fulfilled again during the observations, when the turbulence
conditions change and when the image size varies on the ecartometer as a function of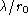 
(details in
Sect. 2.3.3). This correction compensates for the telescope drift during the long time scale measurement,
but low atmospheric frequencies are corrupted.
Data used to evaluate the power spectra of the angle of arrival and of the image tracking accuracy were acquired during a time period of several tens of seconds at a frequency rate higher than the sampling frequency of the servo loop. Typically, the number of data per channel is equal to 8400 in the case of a 30-second recording. The fluctuations of frequency below about 0.03 Hz are therefore filtered by the record process.
The command period of the servo system is equal to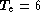 
ms. So, according to Shannon conditions,
the angle of arrival cannot be determined at upper frequencies than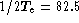 
Hz.
According to the theoretical transfer functions of the servo system (Figs. 4 (click here) to 6 (click here)) simulations of the
performance of the servo-system have been done. Photon flux close to the values measured during the
observations has been taken (see the following section). A theoretical power spectrum of the angle of
arrival characterized by a -2/3 slope in the low frequency domain and a -11/3 slope in the high frequency
domain has been used to represent the incoming perturbation in the servo system. The results of the
simulations are presented in Fig. 9 (click here), which shows the variation of the relative angle of arrival residual
variance as a function of the knee frequency. The relative residual variance is the ratio of that residual
variance which characterized the servo system precision to the variance of the incoming angle of arrival.
Figure 9 (click here) shows that the performance of the servo system is highly sensitive to the turbulence
conditions, represented here by the knee frequency. With a 10 Hz knee frequency and a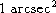 
angle
of arrival variance, the theoretical pointing error (rms) thus equals 0.29 arcsec. Other simulations show
that the accuracy is not really affected by the Signal-to-Noise Ratio, but rather by the bandwidth of the
servo system, limited by the 6 ms command period.
Figure 9: Simulated variation of relative angle of arrival residual variance versus
knee frequency