The angle of arrival is defined as being the normal direction relative to the wavefront mean surface, at
the point of observation and can be expressed as the mean value of the derivative of the disturbed
wavefront at a given aperture (Roddier 1981). The angle 
, measured at any given point on the ground,
is therefore the convolution of the pupil function with this derivative:
where is the component of the angle of arrival on the x direction, 
the phase of the disturbed
wavefront, and 
the pupil function equal to zero outside the aperture.
is a random variable that can be
characterized by its temporal power spectrum 
), where 
is the
temporal frequency. To derive the expression of 
,
the outer scale 
is taken as infinite for
convenience. Its size remains a subject of controversy,
estimations ended up to values from a few
meters (Coulman et al. 1988) to several kilometers (Colavita et al. 1987). Moreover, it is believed to
largely depend on meteorological conditions. The temporal power spectrum for a one-layer
atmosphere can then be written under Taylor hypothesis as follows (Conan 1994):
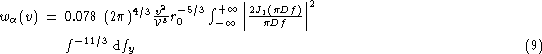
is the average wind speed on the x-axis, J1 is the Bessel function of order 1, and f is the module of
the spatial frequency 
, 
.
Figure 8: Normalized theoretical power spectrum, 
Hz
Figure 8 (click here) shows the spectrum obtained by numerical integration of Eq. (9) with the following values
ascribed to the parameters: aperture diameter D measures 26 cm, Fried parameter r0 10 cm, and wind
velocity on the x-axis 10 m/s. The temporal power spectrum of the angle of arrival shows a 
power law in the low frequency domain, while in the high frequency domain, the spectrum decreases as
(Hogge & Butts 1976;
Martin 1987; Conan et al. 1995).
A power law in 
is mentioned
for the tilt by Roddier et al. (1993) and
Conan (1994) and it concerns the phase component on Zernike
modes z1 and z2. ASSI measures the angle of arrival, expressed as the mean value of the phase first
derivative, implying the power law. In Fig. 8 (click here), a modulation of the profile appears in the high
frequency part of the spectrum. This is due to oscillation induced by the term containing the Bessel
function J1 (Conan 1994). Noise appearing over this modulation is likely to be induced by the
numerical tool. The spectrum is characterized by a frequency (knee frequency) at which a slope-break
marks the separation between the two domains. This knee frequency 
is given by the empirical
formula (Conan et al. 1995):
For the chosen values of and D, equals 11.5 Hz. In practice, the parameter
is the mean
velocity within the different layers of the turbulent atmosphere met by the wavefront. Wind direction
and amplitude fluctuations from a layer to another can induce change around the knee frequency but the
asymptotic behaviors are not modified (Conan et al. 1995). Therefore from experimental power
spectrum knee frequency, the average wind speed in the atmosphere can be estimated.
Estimates of the coherence time t0 are available as a result of the Fried parameter and wind velocity estimations. Knowledge of these parameters is essential in determining temporal bandwidth of optical systems and integration times in interferometric imaging. Using wind speed and r0 estimates obtained from angle of arrival temporal spectra, t0 is given by the formula (Nightingale & Buscher 1991; Davis et al. 1995; Davis & Tango 1995): _0=0.314r_0V.
Equation (11) is only valid in the inertial range of Kolmogorov
(Roddier 1981).
We must note that the optics community has not concurred over a single definition of the coherence
time. Colavita et al. (1987)
define a coherence time T0 such that 
.
Reducing the angle of arrival fluctuations results in stabilization of image position, and the residual
position error 
expressed in arcsecond on the sky can be identified as the observable residual motion
of the image. In this paper, performance of the system is traced by the standard deviation 
of ,
which can be taken as a measure of the tracking accuracy. It can be directly obtained from raw data, or
from the integral of the power spectrum.
Since r0 is directly related to the standard deviation
of the image motion (angle of arrival) on one
axis, it can be written as follows (Tatarski 1971):
