Figure 1 shows a schematic view of I2T (Koechlin & Rabbia 1985). It consists of two 26 cm diameter
telescopes mounted on rail tracks. Output parallel beams are directed toward a central building
(horizontal propagation) where they are combined (Schumacher et al. 1991).
To compensate for the
optical path difference (OPD) due to Earth rotation, a delay line is inserted in the Southern arm of the
interferometer, by means of a cat's eye system. This delay line is movable under computer control with
a 1 m translation stroke (corresponding to 2 m OPD) with a
resolution (Koehler & Manil 1990).
The Northern arm is equipped with a fixed delay line that merely ensures optical and metrological
symmetry. The movable Southern delay line was built in collaboration with Aérospatiale-Cannes and
the Northern cat's eye in collaboration with Matra.
Figure 1: Schematic view of the I2T interferometer
As soon as the diurnal OPD is removed, residual OPD fluctuations can be corrected. They are mostly
induced by atmospheric turbulence and also by mechanical instabilities along the light paths. Note that
due to the seeing conditions on this site, the telescopes are practically never diffraction-limited at
visible and near infrared wavelengths (
).
The main constituents of ASSI are (see Fig. 2 (click here)):
Figure 2: Functional architecture of the ASSI table
- The star tracker, including two active tip-tilt mirrors.
- The fringe tracker, including an OPD fluctuation compensation capability.
- The dispersed fringe analysis channel, used as the science instrument.
The star tracker compensates for fluctuations of the wavefront angle of arrival, and is designed to keep
the two interfering wavefronts parallel to within a fraction of one arcsecond. It is described in
Sect. 2.3.
The fringe sensor allows automatic fringe detection and provides an error signal used for fringe
stabilization.
Since the wavefront distortions are larger in the visible than in the infrared, the fringe tracking system
has been chosen to operate in the near infrared (
to 
). Both pupils are superimposed on
a photon counting avalanche photodiode (APD). The other flat-tint output of the Mach-Zehnder
interferometer feeds an intensified CCD camera for pupil control. The three unknowns of the
interferogram (intensity, visibility and phase) are measured with a temporal sine modulation and a
synchronous demodulation by a specific real time algorithm (Cassaing et al. 1995). The setup is
roughly similar to the Mark III interferometer (Shao et al. 1988).
Only one broadband spectral channel
is used, the coherence length of which is tuned by a spectral filter.
Calculated visibilities are used in automatic fringe detection during a computer-controlled
OPD scan.
This automatic acquisition capability is a marked improvement over visual fringe acquisition as on the
previous I2T (Koechlin & Rabbia 1985).
OPD correction is performed from the calculated phase by a two-stage fine delay line. A piezoelectric
transducer (PZT) with 
OPD dynamic range allows high frequency correction and high OPD
resolution, while a motorized table with 
cm OPD range is used for PZT desaturation when it
exceeds a given position. The main drawback of this system is that the calculated phase suffers from
classical 
wrapping (phase tracking mode), whereas other interferometers are now relying on another
estimator with a wider dynamic (envelope tracking mode). OPD correction is therefore limited by fringe
jumps.
The dispersed fringe analysis channel allows to record fringes in image plane (
-pixel
intensified CCD camera) at a rate of 50 frames per second.
The basic feature is the dispersion of the fringe pattern leading to successive adjacent spectral channels
each roughly 1.1 nm in width. Thus, a large bandwidth is available without reducing the coherence
length (about 
) since the latter is determined by the width of an individual channel.
Up till now, the major limitation to accuracy of visibility measurements in this channel has been
atmospheric degradation. The star tracker is expected to improve the superimposition of the image
patches on the CCD camera so that fringes do not disappear because of poor overlapping, and the fringe
tracker is expected to remove the fringe random motion to improve the accuracy of the measured fringe
visibilities. Longer integration time can then be expected, so that magnitudes larger than the ones
observed in the past could be reached.
Three auxiliary modules are also available: 1) on a monitoring camera, the two stellar images are
observed in a 
arcsecond field, enabling quick detection of such problems as optical aberrations
(telescope defocus for example), photometric dissymmetry or bad seeing conditions ; 2) auxiliary
sources allow internal alignment of the table and external alignment of the pupils prior to each
observation, and are used to determine the internal zero OPD of the table
(Robbe et al. 1994); 3) the
pupil positioning subsystem allows
pupil positions to be kept constant inside the table. Optimal
working conditions dictate that pupil image be kept accurately centered on the active mirror irrespective
of telescope position on each arm. This is achieved by a set of zoom-forming optics movable on each
arm as a function of baseline.
The angle of arrival correction system is made of several parts (see Fig. 3 (click here)).
a) The quad cell
Half of the visible light (
to ) is beam-split from each stellar beam (North and South)
and sent toward a reflecting pyramid in a focal plane where the stellar spot is divided into four parts.
Each part of the spot is directed to a GaAs photon-counting photomultiplier (PMT). The quad cell is
common to both beams: a temporal multiplexing is performed by a rotating chopper which allows to
alternately reimage on the quad cell the observed star from the two telescopes. The integration time is
3 ms successively for each beam, as against a sampling interval of 6 ms. The drawback of the reduced
throughput is that the quad cell is cheaper and that differential angle of arrival cannot arise from drifts in
the quad cell.
b) The calculator
Pulses from the four PMTs which exceed a threshold are synchronously counted with the chopper. At
the end of each integration time, an analog calculator computes the angular error along each axis from
the content of the four counters A, B, C and D
converted to analog signals. The two errors 
and 
are defined by:
This calculator sends offsets to the telescopes when the active mirrors reach user-defined bounds
(correction of telescope drifts).
c) The mirrors
The two tip-tilt voice-coil mirrors were made by Micro-Controle.
They are servo-controlled by an
internal position sensor and their characteristics are as follows:
- clear aperture: 50 mm
- stroke: 
mrad
- resolution: 
rad
- bandwidth: 250 Hz at -3 dB.
This high closed loop bandwidth hides the fact that a mechanical resonance appears at 250 Hz and that
the phase of the transfer function exhibits a quick linear drift (
at 50 Hz).
Taking into account the angular magnification of the ASSI table, the stroke reported on the sky is
arcsec and the resolution is 2 arcsec. The small size of the pupil on the active mirrors (1.4 mm)
is not well suited. It was chosen for previous less efficient mirrors and by the constraint of reimaging
the distant telescope pupil on the mirror.
For star tracking, the error signal from the internal position sensor is replaced by the error measured by
the quad cell. An analog tunable gain allows the user to optimize the bandwidth for each axis, according
to turbulence and noise conditions.
d) The interface
The calculator and the mirrors are interfaced with a PC in charge of the whole ASSI operation (user
interface and fringe tracking computation). This PC allows to initialize the analog calculator,
handshakes with the telescopes for star acquisition, moves the mirrors for optical adjustment or on-line
calibration, controls the chopper, stores files of data with either the 8 PMT counts or the 4 quad cell
signals or the 4 mirror positions.
In closed loop, the residual error is limited by the quad cell noise, the mirror transfer function phase
rotation and the quad cell sampling rate. A bandwidth of 63 Hz in closed loop at -3 dB can be reached
at high light level with the 330 Hz chopper (165 Hz sampling frequency). Figures 4 to 6 show the
open loop transfer function, the closed loop transfer function and the rejection transfer function,
determined by numerical simulations (based on the temporal characteristics of the loop including a 1.5
ms mean delay and the mechanical modeling of the mirror) and consistent with the laboratory
performance. The closed loop transfer function shows the ratio between the mirror position and the
atmospheric perturbation (Demerlé et al. 1994).
In the low frequency domain, the mirror follows
(corrects) the perturbation. In the high frequency domain, beyond the cutoff frequency, the correction is
inefficient. Between the two, there is a resonant regime in which the mirror movement is slightly
stronger than the perturbation.
The closed loop transfer function (in modulus) does not show the residual error between the
perturbation and the correction, which creates a residual error. The relevant curve is the rejection transfer
function which plots the ratio of the residual error to the incoming perturbation (Fig. 6 (click here)). Up to the 0
dB bandwidth (22 Hz), the perturbation is attenuated: this is the goal of the servo system. Beyond the
bandwidth, the perturbation is unaffected, or even amplified near the resonance. For optimum operation,
since atmospheric perturbation is mainly concentrated in low frequencies, the rejection bandwidth
should be greater than the atmospheric cutoff frequency (see Sect. 3).
Figure 4: Open loop transfer function determined by numerical simulations
Figure 5: Closed loop transfer function determined by numerical simulations
Figure 6: Rejection transfer function determined by numerical simulations
As given by Eq. (1), the position of the star image is given by a combination of the four integrated
intensities. Assuming small image displacement and image size much smaller than quadrant size, the
position error is related to the image position (xi, yi) by an expression of the form:
where wi is the full width at half maximum (FWHM) of the star image. The angle of arrival
can therefore be calculated by:
where f is the focal length of the optical system and G the magnification. Let us underline that to
convert position error into an angle, the star image FWHM must be known. This is the case, for
instance, if the star image is unresolved and limited by the telescope diffraction. The image size is then
given by:
where D is the telescope diameter.
But, with the ASSI + I2T experiment, the telescope diameter is often larger than r0 in the spectral band
of the star tracker system. The star image is therefore seeing limited. The FWHM is roughly given by
(Yura 1973):
wi depends on the seeing conditions, and the quad cell response too
(Ma et al. 1989). Therefore, in such
a case, wi is unknown.
The problem induced by the unknown FWHM is uncertainty as to the value of the loop gain of active
control (Eq. (3)). Therefore the loop gain has to be calibrated on the star image itself before closing the
loop, and readjusted during observation. An alternative way is to defocus the star image on the quad cell
in order to keep a constant spot size.
Yet another problem affects the quad cell response: the position measurement is nonlinear for a wide
angle. Equation (2) is only valid for small displacements. For a wide angle, the signal saturates
(Gerson & Rue 1989).
As we just mentioned, optimization of the control loop must take into account the specific conditions
of turbulence met during a given observation, and this of course cannot be achieved once for all at the
internal optimization stage. To that aim, an additional (analog) gain has been included in the control
loop, and has to be time-adjusted in order to preserve the optimal characteristics. Criterion of this
adjustment is the minimizing of the observed standard deviation of the residual error 
, recorded
during a few tens of seconds. It turned out that the response of the control loop is pretty sensitive to
this adjustment which should be made frequently in the course of observation in connection with the
time evolution of the turbulence parameters, Fried parameter r0 and coherence time t0. As an example,
Fig. 7 (click here) shows two sequences of residual errors on the X and Y axes of the Northern mirror obtained
over 10 seconds on the 13th of December 1994, respectively in open loop and in closed loop mode,
with adjusted servo-control gains. In open loop, the spot diagram size is about 0.9 arcsec while, in
closed loop, it is about 0.3 arcsec. These values show the importance of the servo tracker in terms of
minimizing the angle of arrival effect.
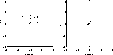
Figure 7: Open loop and closed loop residual errors on the X and Y axes of the Northern mirror with
adjusted servo-control gains (12/13/94 - 10 seconds)
We present here the expression of the measurement error due to different sources of noise like photon
noise, background and electronic noise. Let 
be the number of detected photons per telescope during
the exposure time, we have 
. The expressions of the angle of arrival variance are
deduced from Eqs. (1), (3) and (5). For photon noise, we have:
and for electronic noise:
where 
is the number of electrons of noise per quadrant. For background noise, Eq. (7) can be
used with 
as the number of background detected photons. Equations (6) and (7) are similar to the
one given by Tyler & Fried (1982). They are also relatively close to the expressions derived in the
case of a Shack-Hartmann wavefront sensor (Rousset 1994).
We observe that the spread of the star image due to the seeing severely limits the sensitivity of the quad
cell detector. The best performance is obtained for diffraction-limited images. For the I2T + ASSI
experiment generally D > r0. Thus, measurement noise depends on seeing conditions.
