and
In this appendix, the reliability of null-correlation approach
in order to estimate the slope aD of the DTF relation
is discussed.
In a first step,
it is shown that
the non-observable
variable 
is not
correlated with p
as long as hypotheses 
and 
are satisfied.
Particularly, this property does not depend on the selection function on
m and p.
In a second step, the correlation between p and the observable
variable X:
is investigated.
The presence of radial peculiar velocities such as
the ones assumed in 
indeed correlates
p and X. However, it is shown that
the amplitude of this effect can be weakened by
selecting only distant galaxies of the sample. It is not
surprising since the term
in Eq. (C1 (click here))
becomes negligible for distances r large enough.
Such a subsampling can be performed by
discarding galaxies of the observed sample which have
a distance estimate
less than
a given r*. It corresponds to introduce an extra selection
function 
defined as follows:
Note that introducing this extra selection effect does not
alterate the result
. On the other hand,
a wrong value of the
DTF slope (i.e. 
) correlates p and
:
where
is the square of
standard deviation
of p. The null-correlation approach thus consists to
adopt the value of the parameter a verifying
as the correct estimate
of the slope aD of the DTF relation.
It is proven below that
as long
as assumptions and are satisfied
by the sample. Rewriting the non-observable variable X0 in
terms of m, p and 
gives 
. In terms of 
, it
reads 
where
was previously defined
Eq. (9 (click here)). Since 
and 
are
constants,
. The null-correlation between
p and can be shown by replacing
by 
and using the probability
density 
of Eq. (5 (click here))
expressed in terms of p, m and :
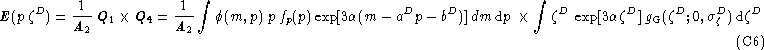
where the normalisation factor A2 reads:
It thus turns out that
, which implies
.
This result
is insensitive to the shape
of the selection function 
in m and p and
to the theoretical distribution function fp(p) of
the variable p.
The term
entering into Eq.
({C3 (click here)) does not vanish since p is correlated
with distance r. However,
its amplitude can be reendered arbitrarily small
by adding an extra selection effect such as the one mentioned
Eq. (C2 (click here)). This feature is illustrated
by the following example.
It is assumed that:
,
and are satisfied by the sample.
(i.e. 
).
where
is the Heaveside distribution function,
if 
and 
otherwise).
proposed Eq.
(C2 (click here)). By introducing 
such that
, 
rewrites
. Adding this extra selection function
,
the probability density
of Eq. (11 (click here)) reads:
describing the sample is
fully specified, calculations of quantities of interest can
be performed analytically or by using numerical simulations.
Hereafter, cumbersome intermediate calculations have been
deliberately omitted and we just furnish the ultimate
analytical expressions of these quantities.
In order to evaluate the amplitude of the term
entering Eq.
({C3 (click here)),
is expanded in Taylor's series up to
order 2:
It implies that the covariance may be expanded as follows:
The calculations give for the terms 
and 
:
where the functions 
and 
are defined
Eq. (C14 (click here)) and Eq. (C15 (click here)). For a given cut-off in
distance estimate , the contribution of
and to 
has to be compared with 
appearing in Eq. (C3 (click here))
when a wrong value of the DTF slope is adopted.
This term 
reads:
where the function 
is defined Eq. (C19 (click here)) and
and 
Eqs. (C14 (click here), C15 (click here)). Finally, the last quantity of interest
is
the ratio 
of selected objects within the observed
sample. This ratio is equal to the normalisation
factor 
divided by
, i.e. the normalisation
factor of the sample when no extra selection effect is
present (r*=0 or 
).
It reads in function of the extra cut-off in distance estimate
introduced Eq. (C8 (click here)) as follows:
where
is defined Eq. (C18 (click here)) and
the
function is introduced Eq. (C17 (click here)).
NOTATIONS:
and , function of the extra cut-off
and of an integer N, are defined as follows:
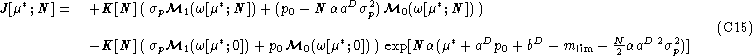
where K(N), function of an integer N, is:
,
and
functions reads:
and , function of the extra cut-off
and of an integer N, is:
The function , involved in the calculation of
, is defined as follows:
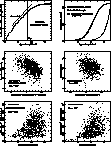
Figure 4:
Mathewson spiral field galaxies sample versus simulated sample