

Up: Calibration of the
The spiral field galaxies sample of
Mathewson et al. 1992 is a composite sample of
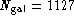 spiral galaxies lying in the field
(galaxies identified as cluster members have
been excluded of this catalog). It covers the south hemisphere
and extends in redshift up to
spiral galaxies lying in the field
(galaxies identified as cluster members have
been excluded of this catalog). It covers the south hemisphere
and extends in redshift up to  km s-1 with
an effective depth of about
km s-1 with
an effective depth of about 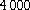 km s-1.
Selection effects in observation are not trivial to model
since sampled galaxies have been
firstly selected in apparent diameter before Mathewson et al.
apply their own selection criteria (minimum limits in
inclination and velocity rotation). Some
galaxies inherited from others observational programs
have been also included in the sample.
The data used hereafter in the analysis are:
km s-1.
Selection effects in observation are not trivial to model
since sampled galaxies have been
firstly selected in apparent diameter before Mathewson et al.
apply their own selection criteria (minimum limits in
inclination and velocity rotation). Some
galaxies inherited from others observational programs
have been also included in the sample.
The data used hereafter in the analysis are:
- the apparent magnitude 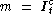 where
where 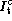 is
the total I-band apparent magnitude corrected for internal
and external extinction and K-dimming (Col. (6), second row in
Mathewson et al. 1992).
is
the total I-band apparent magnitude corrected for internal
and external extinction and K-dimming (Col. (6), second row in
Mathewson et al. 1992).
- the log line-width distance indicator 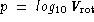 where
where
 is the maximum velocity of rotation of
the spiral galaxy (Col. (9) in
Mathewson et al. 1992).
is the maximum velocity of rotation of
the spiral galaxy (Col. (9) in
Mathewson et al. 1992).
- the redshift 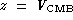 in km s-1 unit expressed
in the CMB velocity frame (Col. (11), first row in
Mathewson et al. 1992).
in km s-1 unit expressed
in the CMB velocity frame (Col. (11), first row in
Mathewson et al. 1992).
The application is presented as follows.
In Sect.
D.1 (click here) is explained how numerical simulations, used
throughout the analysis for quantifying the amplitude of errors bars
and velocity biases, are performed. Section
D.2 (click here) is devoted to test on the calibration
parameters proposed by Mathewson et al. 1992. Finally, NCA
calibration of the Mathewson field galaxies sample is performed
Sect. D.3 (click here).
Accuracies of the NCA calibration parameter estimators
are herein calculated by using numerical simulations.
Reliability of the values of such standard deviations
is of course
closely related to the way simulated samples succeed in
reproducing the characteristics of the real sample
under consideration. A preliminar study of the Mathewson
field galaxies (MAT) sample characteristics is thus required.
On Fig. 4 (top left) is shown the decimal logarithm
of the cumulative count in function of the apparent magnitude
m for the MAT sample. It turns out that
the completeness in
magnitude of the MAT sample is violated beyond  ,
corresponding to about 1/5 of the total number of sampled galaxies.
Observational selection effects are then more complex than
a mere cut-off
,
corresponding to about 1/5 of the total number of sampled galaxies.
Observational selection effects are then more complex than
a mere cut-off 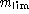 in apparent magnitude. In order
to mimic the real selection effects in observation affecting
the MAT sample, simulations are built in two steps.
in apparent magnitude. In order
to mimic the real selection effects in observation affecting
the MAT sample, simulations are built in two steps.
A virtual sample, complete in apparent magnitude up
to 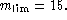 , is firstly
generated assuming the following characteristics:
, is firstly
generated assuming the following characteristics:
- Variable p is generated according to a gaussian distribution
function 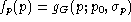 .
.
- Variable  , accounting for the intrinsic scatter of
the DTF relation, is generated according
to a gaussian distribution function
, accounting for the intrinsic scatter of
the DTF relation, is generated according
to a gaussian distribution function
 .
.
- The absolute magnitude  is then formed, with
aD and bD the slope and the zero-point of the DTF relation.
is then formed, with
aD and bD the slope and the zero-point of the DTF relation.
- Variable 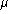 is generated according to an exponential
distribution function
is generated according to an exponential
distribution function  and such that
and such that
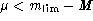 (i.e. distances are thus uniformly distributed in space).
(i.e. distances are thus uniformly distributed in space).
- The redshift  with H0
the Hubble constant in km s-1 Mpc-1 is finally formed
according to the pure Hubble flow hypothesis.
with H0
the Hubble constant in km s-1 Mpc-1 is finally formed
according to the pure Hubble flow hypothesis.
Adopted values for the parameters
p0,
 ,
,
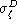 ,
aD,
bD and
H0,
as well as their corresponding "zero-points" B and B*
introduced Eqs. (9 (click here), 20 (click here)),
are given Table 1.
,
aD,
bD and
H0,
as well as their corresponding "zero-points" B and B*
introduced Eqs. (9 (click here), 20 (click here)),
are given Table 1.
The next step is to extract from this virtual sample
a subsamble of 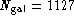 which has the same distribution in
m and p than the observed distribution of the MAT
sample. In effect this selection is achieved as follows.
The m-p
plane is divided in boxes box(i) of equal size and
the number n(i)
of MAT
galaxies belonging to each box box(i) is memorized.
Boxes box(i) are afterwards filled with galaxies belonging to
the virtual sample while the observed n(i) are not reached.
This selection procedure ensures that the m-p distribution
of the simulated samples is approximately identical
to the observed one. It corresponds to introduce a
complex selection function
which has the same distribution in
m and p than the observed distribution of the MAT
sample. In effect this selection is achieved as follows.
The m-p
plane is divided in boxes box(i) of equal size and
the number n(i)
of MAT
galaxies belonging to each box box(i) is memorized.
Boxes box(i) are afterwards filled with galaxies belonging to
the virtual sample while the observed n(i) are not reached.
This selection procedure ensures that the m-p distribution
of the simulated samples is approximately identical
to the observed one. It corresponds to introduce a
complex selection function  in m and p
directly derived from the data.
in m and p
directly derived from the data.
|
| | | | | | | |
|
p0 |
 |
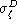 |
aD |
bD |
H0 |
B |
B* |
| | | | | | | |
|
1.82 |
0.2 |
0.35 |
-7. |
-5.3 |
85 |
0.0097 |
0.0106 |
Table 1:
Adopted values for the parameters of the
simulations

Figure 5:
Accuracies of NCA estimators and amplitudes of velocity biases:
(Top left) Ratio R(r*) of selected galaxies within
the simulated
samples function of the extra cut-off in distance estimate
r*(aD,B*).
(Top right) Standard deviation for the correlation
coefficient  and velocity biases created by GA,
Bulk and Maxwellian flows.
(Bottom left) Standard deviation for NCA slope estimator
and velocity biases created by GA,
Bulk and Maxwellian flows.
(Bottom left) Standard deviation for NCA slope estimator
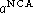 and velocity biases created by GA, Bulk and
Maxwellian flows.
(Bottom right) Standard deviation for NCA "zero-point" estimator
and velocity biases created by GA, Bulk and
Maxwellian flows.
(Bottom right) Standard deviation for NCA "zero-point" estimator
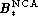 and velocity biases created by GA, Bulk and
Maxwellian flows
and velocity biases created by GA, Bulk and
Maxwellian flows
Figure 4 (top right) shows the cumulative count in apparent
magnitude for the MAT sample and for a simulated sample.
The cumulative count expected
for a sample complete up to 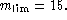 is also shown for comparison. Figures 4 (center left) and
(center
right) show respectively the distribution in the m-p plane
of the MAT sample and a simulated sample. The difference
between these two distributions are due to discretization
effects which appear when applying the boxes algorithm.
Figures 4 (bottom left) and (bottom right) show respectively
the m-z distributions for the MAT sample and for
a simulated sample. The fact that simulated sample
distribution approximately reproduces the observed one
is encouraging. It means that the working hypotheses assumed
when generating simulated samples, such as the uniform spatial
distribution of galaxies, are close to be verified by
the Mathewson field galaxies sample.
The likeness to data can certainly be improved,
by choosing a more realistic shape for the luminosity
function for example (i.e. the p distibution fp(p)),
but is out of the scope of this study. Hereafter, these
simulated samples
will be considered as fair representatives of
the observed catalog.
is also shown for comparison. Figures 4 (center left) and
(center
right) show respectively the distribution in the m-p plane
of the MAT sample and a simulated sample. The difference
between these two distributions are due to discretization
effects which appear when applying the boxes algorithm.
Figures 4 (bottom left) and (bottom right) show respectively
the m-z distributions for the MAT sample and for
a simulated sample. The fact that simulated sample
distribution approximately reproduces the observed one
is encouraging. It means that the working hypotheses assumed
when generating simulated samples, such as the uniform spatial
distribution of galaxies, are close to be verified by
the Mathewson field galaxies sample.
The likeness to data can certainly be improved,
by choosing a more realistic shape for the luminosity
function for example (i.e. the p distibution fp(p)),
but is out of the scope of this study. Hereafter, these
simulated samples
will be considered as fair representatives of
the observed catalog.
Figure 5 visualizes results obtained on these simulated samples.
At the top left is plotted the ratio R(r*) of selected galaxies
within a simulated sample when the subsampling in distance
estimate (i.e. 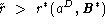 ) is applied.
Standard statistical deviation of the correlation coefficient
between p and the velocity estimates
) is applied.
Standard statistical deviation of the correlation coefficient
between p and the velocity estimates 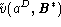 in function of the cut-off in distance estimate r*
is shown in Fig. 5 (top right). Standard deviation
(i.e. accuracy) of
the NCA slope estimator
in function of the cut-off in distance estimate r*
is shown in Fig. 5 (top right). Standard deviation
(i.e. accuracy) of
the NCA slope estimator
 and of the NCA "zero-point"
and of the NCA "zero-point" 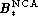 are
respectively presented Figs. 5 (bottom left) and (bottom right).
If no peculiar velocity field is present (i.e. pure Hubble
flow hypothesis, as it is the case for simulated samples), we see
that
are
respectively presented Figs. 5 (bottom left) and (bottom right).
If no peculiar velocity field is present (i.e. pure Hubble
flow hypothesis, as it is the case for simulated samples), we see
that 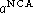 and
and 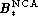 estimators are not biased, as it was
previously proven appendices B and C (averaged over 1000
simulations, their values coincide with the input slope and
"zero-point" of the simulated sample). It illustrates one of the
potentialities of the null-correlation approach for calibrating TF
like relations, i.e. its insentivity to observational selection
effects in apparent magnitude m and log line-width distance
indicator p.
For these simulated samples supposed to mimic the
Mathewson field
galaxies sample (
estimators are not biased, as it was
previously proven appendices B and C (averaged over 1000
simulations, their values coincide with the input slope and
"zero-point" of the simulated sample). It illustrates one of the
potentialities of the null-correlation approach for calibrating TF
like relations, i.e. its insentivity to observational selection
effects in apparent magnitude m and log line-width distance
indicator p.
For these simulated samples supposed to mimic the
Mathewson field
galaxies sample (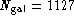 ), accuracy
), accuracy
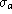 of the NCA slope estimator
of the NCA slope estimator 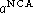 sounds clearly good:
sounds clearly good: 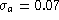 or
or  of aD if all the sample is selected,
of aD if all the sample is selected,  if half of the nearby galaxies of
the sample are discarded (i.e. R(r*)=0.5
or
if half of the nearby galaxies of
the sample are discarded (i.e. R(r*)=0.5
or  km s-1)
and
km s-1)
and 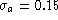 at
at 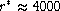 km s-1
(i.e. R(r*)=0.25)
km s-1
(i.e. R(r*)=0.25)  .
The same remark holds for the NCA "zero-point"
.
The same remark holds for the NCA "zero-point" 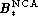 accuracy
accuracy
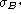 ,
,  or
or  of B*
at r*=0 and
of B*
at r*=0 and  at
at 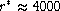 km
s-1.
km
s-1.
Influence of peculiar velocity field on the NCA estimators
is analysed using three examples: "Great Attractor" (GA) flow,
constant or bulk flow and gaussian random or Maxwellian flow.
In order to take into account the peculiarity
of the 3D spatial distribution of the Mathewson field galaxies sample,
biases created by these flows have
been calculated by comparing the estimates of 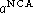 ,
, 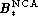 and
and
 when one of these velocity field is added
to the observed redshifts of the MAT sample, with these
estimates for the real MAT sample. The Maxwellian flow
has a velocity agitation of
when one of these velocity field is added
to the observed redshifts of the MAT sample, with these
estimates for the real MAT sample. The Maxwellian flow
has a velocity agitation of  km s-1 and
the bulk flow has been chosen to point toward direction
l=310 and b=20 in galactic coordinates with an amplitude
of 500 km s-1. The GA
flow
km s-1 and
the bulk flow has been chosen to point toward direction
l=310 and b=20 in galactic coordinates with an amplitude
of 500 km s-1. The GA
flow  is the one of Bertschinger et al.
(1988), centered at a distance of
is the one of Bertschinger et al.
(1988), centered at a distance of 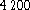 km s-1 toward
l=310 and b=20 and creating an infall velocity for our Local
group of 535 km s-1.
km s-1 toward
l=310 and b=20 and creating an infall velocity for our Local
group of 535 km s-1.
Figure 5 (bottom left) illustrates particularly well
the discussion of Sect. 3.1 (click here) which
was based on analytical results.
Biases on the NCA slope estimate
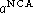 created by the presence of
Maxwellian and Bulk flows become negligible when
nearby galaxies of the MAT sample are discarded
using the subsampling procedure in distance estimate
(say herein for r* > 3000 km s-1).
Influence of GA flow can be controled likewise.
In practice, large values of the cut-off in distance
estimate r* have to be preferred, of course with
regards to the accuracy and to the r*-dependent statistical
fluctuations affecting the NCA slope estimate at this
distance r*.
created by the presence of
Maxwellian and Bulk flows become negligible when
nearby galaxies of the MAT sample are discarded
using the subsampling procedure in distance estimate
(say herein for r* > 3000 km s-1).
Influence of GA flow can be controled likewise.
In practice, large values of the cut-off in distance
estimate r* have to be preferred, of course with
regards to the accuracy and to the r*-dependent statistical
fluctuations affecting the NCA slope estimate at this
distance r*.
Influences of velocity fields on 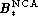 and
and
 are shown respectively in Figs. 5 (bottom
right) and (top right). As expected,
Maxwellian flow does not bias these two quantities. Since
the calibration of the simulated samples was not
performed line-of-sight by line-of-sight, presence
of Bulk flow slightly biases
are shown respectively in Figs. 5 (bottom
right) and (top right). As expected,
Maxwellian flow does not bias these two quantities. Since
the calibration of the simulated samples was not
performed line-of-sight by line-of-sight, presence
of Bulk flow slightly biases 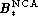 and
and
 . On the other hand, we can
see that GA flow creates a significative bias
on the two quantities (i.e. greater than their standard
deviations). The fact that these biases vanish
for large values of the cut-off in distance estimate r*
is due to the specific form of the GA flow and to
the characteristics of the 3D spatial distribution of
the MAT sample. It cannot be interpreted as a general
feature since the correlation between p and
. On the other hand, we can
see that GA flow creates a significative bias
on the two quantities (i.e. greater than their standard
deviations). The fact that these biases vanish
for large values of the cut-off in distance estimate r*
is due to the specific form of the GA flow and to
the characteristics of the 3D spatial distribution of
the MAT sample. It cannot be interpreted as a general
feature since the correlation between p and  is not expected to vanish when the subsampling in
distance estimate is applied, as it is the case
for the p-X(aD) correlation. Some reasons
may however be advocated for favouring large
values of the cut-off in distance estimate r*.
Since such a subsampling selects preferencially far away
galaxies, a slighter coherence of their peculiar velocities is
expected, consequently to their mutual distances.
Finally, one remarks
that amplitude of the bias created by huge flows such
as the "Great Attractor" is not greater than
is not expected to vanish when the subsampling in
distance estimate is applied, as it is the case
for the p-X(aD) correlation. Some reasons
may however be advocated for favouring large
values of the cut-off in distance estimate r*.
Since such a subsampling selects preferencially far away
galaxies, a slighter coherence of their peculiar velocities is
expected, consequently to their mutual distances.
Finally, one remarks
that amplitude of the bias created by huge flows such
as the "Great Attractor" is not greater than
 , or
, or  of the value of B*.
Same remark for the bias on the correlation coefficient
of the value of B*.
Same remark for the bias on the correlation coefficient
 which is less than
which is less than  whatever the value of the cut-off in distance estimate r*.
whatever the value of the cut-off in distance estimate r*.

Figure 6:
Correlation between p and Mathewson velocity estimates
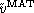
Mathewson et al.1992 have proposed some values
for the DTF calibration parameters. The authors
calibrate the DTF slope aD in the Fornax cluster
(14 galaxies). An estimate of  is
obtained by performing a
linear regression in magnitude. Assuming that the
true distance in km s-1 units of Fornax cluster
is
is
obtained by performing a
linear regression in magnitude. Assuming that the
true distance in km s-1 units of Fornax cluster
is  km s-1, authors derived a value
of
km s-1, authors derived a value
of 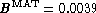 for DTF relative zero-point B.
If H0=85
km s-1 Mpc-1, it implies a value of
for DTF relative zero-point B.
If H0=85
km s-1 Mpc-1, it implies a value of 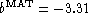 for
the DTF zero-point bD. Averaging over the seven richest clusters
of their catalog, a value of
for
the DTF zero-point bD. Averaging over the seven richest clusters
of their catalog, a value of 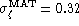 is estimated for the intrinsic scatter of the DTF relation,
which gives a value of
is estimated for the intrinsic scatter of the DTF relation,
which gives a value of  for the
DTF relative "zero-point" B*. No error bars are
proposed for these estimates.
for the
DTF relative "zero-point" B*. No error bars are
proposed for these estimates.
Mathewson et al. DTF calibration parameters are tested in
Fig. 6. Figure 6 (left) shows the correlation between
p and Mathewson et al. peculiar velocity estimate
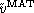 for the
for the 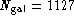 of
the MAT sample. Figure 6 (right) shows variations
of
of
the MAT sample. Figure 6 (right) shows variations
of  with respect to
the cut-off in distance estimate r* and the deviations
from 0 expected when a flow such as the "Great Attractor"
is present. It looks very unlikely that the strong
correlation found between p and
with respect to
the cut-off in distance estimate r* and the deviations
from 0 expected when a flow such as the "Great Attractor"
is present. It looks very unlikely that the strong
correlation found between p and 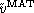 can be explained by the presence of large scale coherent
peculiar velocity field. The same feature is observed
for the p-
can be explained by the presence of large scale coherent
peculiar velocity field. The same feature is observed
for the p- correlation (not shown).
This test leads to question in the validity of the calibration
techniques used by Mathewson et al. when deriving
slope and relative zero-point of the DTF relation.
correlation (not shown).
This test leads to question in the validity of the calibration
techniques used by Mathewson et al. when deriving
slope and relative zero-point of the DTF relation.
As a matter of fact, it is known that the estimator
of the DTF slope aD, obtained in a cluster
by a linear regression on m, is biased by the presence
of observational selection effects on m and p
(see Lynden-Bell et al. 1988 for example).
This bias can be corrected on in theory but a full
description of selection effects in observation is
thus required (see for example Willick 1994),
and so is difficult to realize in practice.
Same kind of remark holds for the relative zero-point
estimate B. Since existing peculiar velocity field models
proposed in the literature are far to be perfect nor
accurate, a room of uncertainty remains when attributing
a true distance to the calibration cluster (an error
of 250 km s-1 for the assumed true distance of Fornax
cluster will imply a relative error of  for the relative zero-point B).
for the relative zero-point B).

Figure 7:
NCA calibration of the Mathewson spiral field galaxies sample:
(Top left) Ratio R(r*) of selected galaxies within
the MAT sample function of the extra cut-off in distance estimate
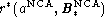 .
(Top right) Correlation
coefficient
.
(Top right) Correlation
coefficient  between p and
NCA peculiar velocity estimate
between p and
NCA peculiar velocity estimate  .
(Bottom left) NCA slope estimate
.
(Bottom left) NCA slope estimate
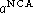 function of the extra cut-off in distance estimate
function of the extra cut-off in distance estimate
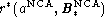 .
(Bottom right) NCA relative "zero-point" estimate
.
(Bottom right) NCA relative "zero-point" estimate
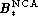 function of the extra cut-off in distance estimate
function of the extra cut-off in distance estimate
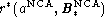

Figure 8:
NCA "zero-point" estimate for  remaining
galaxies of the MAT sample when excluding the GA region
(defined as a conic area pointing toward l=310 and
b=20 with an angular aperture of
remaining
galaxies of the MAT sample when excluding the GA region
(defined as a conic area pointing toward l=310 and
b=20 with an angular aperture of 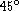 ):
(Left) Standard deviation for NCA "zero-point" estimator
):
(Left) Standard deviation for NCA "zero-point" estimator
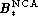 and velocity biases created by GA and Bulk flows.
(Right) NCA "zero-point" estimate
and velocity biases created by GA and Bulk flows.
(Right) NCA "zero-point" estimate
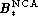 function of the extra cut-off in distance estimate
function of the extra cut-off in distance estimate
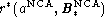

Figure 9:
Top: Redshifts z versus NCA distance estimates
in km s-1 for the MAT sample (left) Outside the GA region
(right) Inside the GA region. Bottom: Peculiar velocity
difference between Mathewson velocity estimates
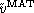 and NCA velocity estimates
and NCA velocity estimates

NCA calibration is herein performed by following the
discussions of Sect. D.1 (click here). The
NCA estimate of the DTF slope aD is obtained from
a subsample selected in distance
estimate beyond 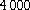 km s-1, which corresponds
to discard about
km s-1, which corresponds
to discard about 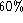 of nearby galaxies
of the MAT sample. NCA estimate of the DTF "zero-point"
B* was achieved using galaxies beyond
of nearby galaxies
of the MAT sample. NCA estimate of the DTF "zero-point"
B* was achieved using galaxies beyond 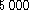 km s-1.
Figure 7 shows the results of the NCA calibration of
the Mathewson field galaxies catalog
km s-1.
Figure 7 shows the results of the NCA calibration of
the Mathewson field galaxies catalog .
.
The value of NCA estimate of the DTF slope aD is
given in Fig. 7 (bottom left):
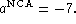 with an accuracy at
with an accuracy at 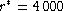 km s-1
given by the numerical simulations of
km s-1
given by the numerical simulations of 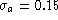 (or in other words
(or in other words  ).
Since this estimate is obtained with a large cut-off
in distance estimate, it is in principle free
of biases created by large scale peculiar velocity
field. Adding to this point that NCA calibration technique
is insentive to observational selection effects on
apparent magnitude m and log line-width distance indicator p,
NCA estimate of DTF slope aD appears as fairly secure.
).
Since this estimate is obtained with a large cut-off
in distance estimate, it is in principle free
of biases created by large scale peculiar velocity
field. Adding to this point that NCA calibration technique
is insentive to observational selection effects on
apparent magnitude m and log line-width distance indicator p,
NCA estimate of DTF slope aD appears as fairly secure.
NCA estimate of the relative "zero-point" B* is shown
in Fig. 7 (bottom right).
The value of  has been arrested accounting
for the more or less stable trend of
has been arrested accounting
for the more or less stable trend of 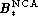 beyond
beyond
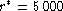 km s-1. To give a value of the
km s-1. To give a value of the
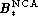 accuracy is a little bit more tricky.
It was previously mentioned that the subsampling procedure
in distance estimate does not remove bias on
accuracy is a little bit more tricky.
It was previously mentioned that the subsampling procedure
in distance estimate does not remove bias on 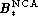 estimator created by the presence of large scale peculiar
velocity field (excepting the case of bulk flows). It turns out
that the value of this bias depends on
the specific geometry and amplitude of the real cosmic
velocity field, and so cannot be estimated without modeling this
velocity field. The amplitude of this bias for the
"Great Attractor" flow model is less
than
estimator created by the presence of large scale peculiar
velocity field (excepting the case of bulk flows). It turns out
that the value of this bias depends on
the specific geometry and amplitude of the real cosmic
velocity field, and so cannot be estimated without modeling this
velocity field. The amplitude of this bias for the
"Great Attractor" flow model is less
than  (or about
(or about  of B*)
for the MAT sample. It means that if the GA flow is real,
error on
of B*)
for the MAT sample. It means that if the GA flow is real,
error on 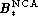 estimator is dominated
by velocity bias rather than statistical fluctuations (accounting
for the
value of the accuracy on
estimator is dominated
by velocity bias rather than statistical fluctuations (accounting
for the
value of the accuracy on 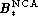 obtained from numerical
simulations). At this stage, other criterion for
calibrating DTF relative "zero-point" B* may be
preferred, for example in constraining the average
obtained from numerical
simulations). At this stage, other criterion for
calibrating DTF relative "zero-point" B* may be
preferred, for example in constraining the average 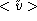 of radial peculiar velocity estimates over the sample
to vanish. Unfortunatly such property
of radial peculiar velocity estimates over the sample
to vanish. Unfortunatly such property 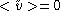 is
theoretically expected for fair samples (i.e. samples large enough
to be representative at any scales of the kinematical fluctuations
of the Universe), but not expected for calalogs
such as the MAT sample.
is
theoretically expected for fair samples (i.e. samples large enough
to be representative at any scales of the kinematical fluctuations
of the Universe), but not expected for calalogs
such as the MAT sample.
Amplitude of velocity bias on the 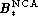 estimator
may however be attenuated by removing of the sample
areas presumed to have a strong kinematical activity.
Such a procedure was achieved by discarding galaxies
of the MAT sample belonging to a cone pointing toward l=310
and b=20 in galactic coordinates with an angular aperture of
estimator
may however be attenuated by removing of the sample
areas presumed to have a strong kinematical activity.
Such a procedure was achieved by discarding galaxies
of the MAT sample belonging to a cone pointing toward l=310
and b=20 in galactic coordinates with an angular aperture of
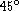 (the GA region). This subsample (i.e. MAT sample, GA
region excluded) contains
(the GA region). This subsample (i.e. MAT sample, GA
region excluded) contains  galaxies.
Figure 8 (left) shows
amplitudes of biases created by bulk and GA flow
when the GA region is excluded of the MAT sample.
Compared to the biases shown in Fig. 5 (bottom left)
for the whole MAT sample, the discarding
procedure looks efficient (if of course, the "Great
Attractor" model of Bertschinger et al. 1988
succeeds in mimicking the real cosmic peculiar velocity field).
Figure 8 (right) shows the NCA estimate
galaxies.
Figure 8 (left) shows
amplitudes of biases created by bulk and GA flow
when the GA region is excluded of the MAT sample.
Compared to the biases shown in Fig. 5 (bottom left)
for the whole MAT sample, the discarding
procedure looks efficient (if of course, the "Great
Attractor" model of Bertschinger et al. 1988
succeeds in mimicking the real cosmic peculiar velocity field).
Figure 8 (right) shows the NCA estimate 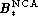 for the MAT sample, GA region excluded.
If the situation improves for
for the MAT sample, GA region excluded.
If the situation improves for  km s-1
(compared
to Fig. 6 (bottom left) showing
km s-1
(compared
to Fig. 6 (bottom left) showing 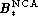 for the whole MAT sample), a residual bias persists
between
for the whole MAT sample), a residual bias persists
between  km s-1 and
km s-1 and 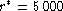 km s-1.
The value of the NCA relative "zero-point"
km s-1.
The value of the NCA relative "zero-point"  has then to be read cautiously, keeping in mind that
it can be affected by a velocity bias (anyway
presumed not to be greater than
has then to be read cautiously, keeping in mind that
it can be affected by a velocity bias (anyway
presumed not to be greater than  )
) .
.
Finally, distance estimate  and velocity estimate
and velocity estimate
 given respectively Eq. (6 (click here)) and
Eq. (20 (click here)) can be inferred using
the NCA calibration parameters
given respectively Eq. (6 (click here)) and
Eq. (20 (click here)) can be inferred using
the NCA calibration parameters 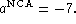 and
and  previously derived.
Figure 9 (left) and (right) show respectively the
redshift z versus the NCA predicted distance
previously derived.
Figure 9 (left) and (right) show respectively the
redshift z versus the NCA predicted distance
 for galaxies of the MAT sample
outside and inside the GA region.
Figure 9 (bottom) illustrates the difference
between the peculiar velocity estimates
for galaxies of the MAT sample
outside and inside the GA region.
Figure 9 (bottom) illustrates the difference
between the peculiar velocity estimates
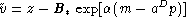 of Mathewson et al. 1992 and
the ones derived in this present appendix.
The averaged velocity difference by bins
of redshift z is plotted function of the redshift.
It turns out that an erroneous input value of the
calibration parameters can interpret, especially at large
redshifts, as fictitious large scale and coherent
peculiar velocity flows. The preliminar calibration step of
Tully-Fisher like relation is thus of crucial
importance for kinematical studies.
of Mathewson et al. 1992 and
the ones derived in this present appendix.
The averaged velocity difference by bins
of redshift z is plotted function of the redshift.
It turns out that an erroneous input value of the
calibration parameters can interpret, especially at large
redshifts, as fictitious large scale and coherent
peculiar velocity flows. The preliminar calibration step of
Tully-Fisher like relation is thus of crucial
importance for kinematical studies.


Up: Calibration of the
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr




