B. Correlation between and

Hereafter, the correlation between p and the velocity estimator given Eq. (20 (click here)) is calculated assuming the following hypothesis:

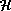• 3) Along a line-of-sight, the distribution of radial peculiar velocities v does not depend on distances r and is a gaussian of mean u and dispersion , i.e. .

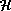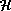Under assumptions 1, 2 and 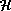3, the probability density 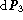of Eq. (11 (click here)) rewrites:
 
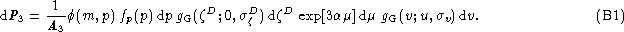
In order to calculate each term involved in the covariance of p and , i.e. , the velocity estimator given Eq. (9 (click here)) is rewritten in terms of variables v, and :
 
Since u is a constant, 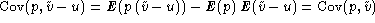. Integrating over the variable v gives for the three quantities , and :
 

 

 
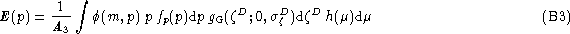
where properties (A5 (click here)a) and (A5 (click here)b) have been used. Replacing by and using definition of B given Eq. (9 (click here)), Eqs. (B3 (click here), B4 (click here), B5 (click here)) expressed in terms of p, m and read:
 

 

 
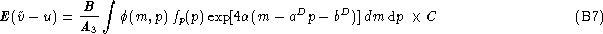
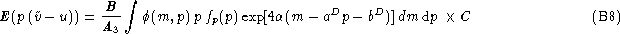
where the constant C is defined as follows:
 
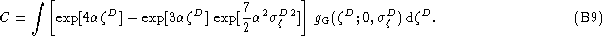
By using properties (A4 (click here)) and (A5 (click here)a), it is found that integral of Eq. (B9 (click here)) vanishes. It thus implies that C=0, , , 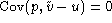and finally . This result does not depend on the shape of the selection function in m and p, on the theoretical distribution function f_p(p) of the variable p and on the mean radial peculiar velocity u along the line-of-sight. 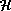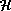For a sample of galaxies satisfying hypotheses 1, 2 and 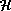3, it thus turns out that the observable p is not correlated with the velocity estimator as long as the model parameters entering into via Eq. (9 (click here)) are correct. On the other hand, if a wrong value is assumed for one of these calibration parameters, say for example that a^D, b^D and 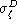are correct but not the Hubble constant , the covariance between p and gives:
 
which does not vanish since existing selection effects on apparent magnitude m correlate variables p and (i.e. for selected galaxies, observable p increases in average with the distance estimator ). This point motivates the use of a null-correlation approach in order to calibrate Tully-Fisher like relations.