Most of the wavelet coefficients of the transform
of a noiseless signal are close to zero. Therefore the most obvious way of
filtering in the wavelet domain is to identify those wavelet coefficients
that are significantly non-zero against the noisy background (Donoho &
Johnstone 1994). This motivates the method of hard
thresholding according to which only the significantly non-zero
coefficients are retained and all others rejected:
where the wm are wavelet coefficients of the noisy signal, the Wm are
the filtered wavelet coefficients, 
is the estimated standard
deviation of the noise at the appropriate scale m, and k is a freely
selectable factor which defines the level of confidence for the preserved
coefficients. Non-orthogonal wavelets reduce the with
increasing m, and hence we have to estimate it for each scale separately
(Starck & Bijaoui 1994).
We now briefly introduce the principles of some more sophisticated de-noising methods with which we later compare our own method. The first method was developed by Donoho (1992a,b). It is based on the so-called wavelet shrinkage technique. In addition to the application of a threshold criterion, the wavelet coefficients are shrunk towards zero. Donoho & Johnstone (1992, 1993, 1994) provide several algorithms based on statistical arguments to determine the level of shrinkage.
Figure 1: Two-level decomposition of a Stokes V spectrum with a noise level
of 
. The corrupted signal is plotted on the
left, the coefficients of the first level of decomposition are plotted in
the central column. The coefficients of the wavelet transform of each of
the scales in the central column are plotted on the right (second level of
decomposition). The two-level decomposition reveals some of the uncorrupted
signal at scales 13 to 15 which is absent at scale 1. Hence truncating
scales 11 to 15, instead of scale 1, can recover features of the
uncorrupted signal which are lost if scale 1 is
truncated
Another set of noise-reduction methods have been proposed by Starck & Bijaoui (1994). They employ the so-called à trous algorithm to perform the wavelet transformation based on linear or cubic spline functions. They apply different filter criteria which include information on wavelet coefficients of different scales (hierarchical filtering). In addition, they use an iterative reconstruction (adaptive filtering) to find a signal whose wavelet transform is as close as possible to the original set of thresholded coefficients (see also Starck & Murtagh 1994 and Starck et al. 1995 for further details).
The final noise reducing technique to which we compare our method was developed by Bury et al. (1996) and is also based on the à trous algorithm. They apply an iterative structure detection algorithm in the scale-space plane to extract the significant coefficients from the noisy wavelet transform.
In the next section we present a somewhat different approach to the problem of noise reduction using wavelet-based techniques. Instead of applying a suitable selection criterion to determining the significant coefficients of a certain scale we extract the underlying spectral features of a noisy scale by simply transforming it again using the same wavelet base (wavelet-packets analysis). The transformed signal is then de-noised by a simple hard thresholding criterion. Details are given in the next section.
Noise is mainly concentrated at the finest scales of a signal transformed using non-orthogonal wavelets, i.e. the signal-to-noise ratio (SNR) decreases towards the finer scales. If the noise level of the original signal is sufficiently high, the finest scales are completely dominated by noise. As an example consider the noisy signal in the left part of Fig. 1 (click here) (details about the signal are given later). The wavelet coefficients of the noisy signal are plotted at the center, with frequency decreasing from top to bottom. The highest frequency coefficients, i.e. the top row, are completely dominated by noise. As we demonstrate later, however, there is a considerable signal hidden in that noise. Simply truncating the wavelet coefficients at these scales either rejects the real signal along with the noise or leaves so much noise that the signal is still not recognizable. This dilemma is resolved using the splitting algorithm of a wavelet-packets analysis (Wickerhauser 1991). Each scale (frequency) may itself be considered to be a noisy signal for which we wish to separate the noise from the signal. We do this by transforming (decomposing) the wavelet coefficients at each scale, again, exactly in the same manner as we transformed the original signal. The coefficients resulting from this second set of transformations are shown on the right side of Fig. 1 (click here): each scale of the singly transformed signal gives rise to (in this case) 5 scales in the doubly transformed or twice decomposed signal.
Figure 2: a) Finest scale
of the non-orthogonal wavelet transform of
a noisy signal (scale 1 of Fig. 1 (click here)). b)
Same scale of the uncorrupted original signal. c) Reconstructed scale
after a three-level-decomposition. Clearly there is little chance of
recovering the uncorrupted pattern out of the noisy signal a) by
simply truncating at a certain threshold value. In contrast the
reconstructed scale c) is a good approximation of the uncorrupted
scale b)
For greater clarity we number the scales of the different decompositions as follows: The scales after the first transformation are numbered 1, 2, ... 5 (from finest to coarsest). After the second level of decomposition we number them as follows: 11, 12, ... 15 (transforms of scale 1), ..., 51, 52, ... 55 (transforms of scale 5). The tree-like arrangement of the individual scales which results from a two-level decomposition of a Stokes V (i.e. circularly polarized) spectrum is illustrated in Fig. 1 (click here).
Consider scale 1 of Fig. 1 (click here). It is completely dominated by noise. Simple thresholding will set each coefficient to zero, because none lies significantly above the background noise. Consequently the restored signal will be considerably altered in the high frequency range, i.e. in the peaks of the spectral lines. After the second transformation the hidden signal has partially been separated from the noise and has become clearly visible at the scales 14 and 15 and can still be detected in scale 13, although just barely. If we now truncate all the wavelet coefficients of the twice decomposed signal under a hard threshold, then we can reduce the noise by almost the same amount as after the first transformation, while preserving much more of the uncorrupted signal, particularly at high frequencies. It is possible to recover even more of the original signal by transforming scales 11-55 once more (three-level decomposition). The degree to which a three-level decomposition can restore scale 1 is shown in Fig. 2 (click here). Note the remarkable similarity of the reconstructed coefficients (Fig. 2 (click here)c) to the original, uncorrupted coefficients (Fig. 2 (click here)b).
Due to its high redundancy the base of non-orthogonal wavelets has the highly desirable property that it allows the main features of the uncorrupted signal to be recognized even after several decompositions of the noisiest scales. So instead of truncating the coefficients of the finest scales directly it is worth transforming them once again and performing the truncation on the coefficients of the second (or third) decomposition level.
Generally, by truncating the coefficients of a higher level of decomposition, it is possible to restore features of the uncorrupted signal at scales of lower levels, which were originally drowned in the noise. This is especially effective for the finest scales whereas the coarser scales have a larger SNR and hence can be truncated directly at the first level of decomposition without affecting their information content significantly.
In the present paper we truncate the coefficients on the basis of a simple
hard thresholding criterion. Since we are dealing with non-orthogonal
wavelets, we need to know the standard deviation of noise at each scale
. Due to the linearity of the wavelet
transformation, i.e.
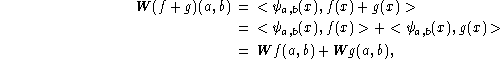
this can be obtained from the transformation of a signal that consists
purely of noise. Strictly speaking we do the following. First we determine
the standard deviation of the noise of the corrupted signal (white Gaussian
noise in the illustrated case). Then this value is used to create a signal
of pure, e.g., white Gaussian noise to which our splitting scheme is
applied. Finally, we get an estimate of the standard deviation of noise at
scale m of the corrupted signal, called , by calculating the
standard deviation of the pure noise, called , of
that scale. Such a scheme has already been applied by Starck & Bijaoui
(1994). We set the threshold value to 
. The
factor k determines the confidence level of the preserved coefficients. In
general we set k=3, which results in a level of confidence of 99.7%.
Figure 3: a) Uncorrupted Stokes V spectrum. b) Corrupted version
with artificially added noise with 
. c)
Fourier smoothed spectrum. It shows clearly the typical random
oscillations within the low frequency parts of the spectrum. d)
Wavelet-packets de-noised version, using a three-level decomposition. The
continuum is now clean and even a number of small features of the original
spectrum are at least qualitatively recovered
We test the various methods on intensity (Stokes I) and net circular
polarization spectra (Stokes V) of solar features recorded with the Fourier
Transform Spectrometer (FTS) installed at the McMath Pierce facility at Kitt
Peak. The data are ideal for testing various de-noising techniques for a
number of reasons. They have a very low noise level (as low as
in some parts of the spectrum; 
is the continuum
intensity), so that de-noising techniques can be tested rigorously. They
have a spectral resolving power of 
, so that the high
frequencies present in the original solar spectrum have not been
significantly suppressed by the instrument. They cover a broad wavelength
range with different types of spectral features. Also, both Stokes I and Stokes V\
spectra were recorded. In the following we first concentrate on Stokes V since
it shows higher frequencies and thus poses a larger challenge to de-noising
techniques, particularly since the data are sampled close to the Nyquist
frequency. The data are described in detail by Stenflo et al.
(1984) and Solanki (1987).
We first corrupted the spectra by adding artificial white Gaussian noise
whose standard deviation scales as the inverse of the square root of the
reference spectrum intensity. Such a noise spectrum is a good representation
of Poisson distributed photon noise in the limit of many photons (which is
fulfilled by the present data)
. These noisy spectra then served as input
data for the de-noising algorithms described in Sects. 3.1 (click here) and
3.2 (click here).