

Up: Noise reduction in
The Fourier transformation decomposes a signal into sines and cosines of
different frequencies. The wavelet transformation acts similarly, but
instead of non-local, strictly periodic sines and cosines, it uses a set of
spatially localized functions 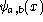 called wavelets (Daubechies
1988; Meyer 1993; see Press et al. 1992
for a simple introduction to the subject). The wavelets are constructed by
translating and dilating a mother wavelet
called wavelets (Daubechies
1988; Meyer 1993; see Press et al. 1992
for a simple introduction to the subject). The wavelets are constructed by
translating and dilating a mother wavelet 

where the scale parameter a plays the role of a frequency and b is the
position parameter. By increasing a, the wavelet 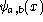 is
broadened, while changing b translates it along the x-axis. The set of
parameters (a,b) describes a point in the so called scale-space plane.
is
broadened, while changing b translates it along the x-axis. The set of
parameters (a,b) describes a point in the so called scale-space plane.
The continuous wavelet transform of a function f(x),
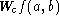 , is defined by
, is defined by

It is invertible (Grossmann & Morlet 1984) and the function
f(x) can be recovered by evaluating the double integral:

Note that, unlike the Fourier transform, the wavelet transform is not\
its own inverse. This implies that a signal may be transformed several times
using wavelets and be further decomposed at each transformation. Such a
sheme of repeated application of the wavelet transform leads to the
splitting algorithm of a wavelet packets analysis (Wickerhauser
1991, 1994; Chui 1992b) which lies at the heart of the
technique we propose.
For practical applications, the continuous set of parameters (a,b), must
be discretized (Daubechies 1988; Mallat 1989).
The parameterization of the discrete (a,b) pairs is of crucial
significance to the discrete wavelet transform and especially to the
stability of the reconstruction algorithm (Daubechies 1990).
For most of the parameterizations of (a,b) the set of
 is highly redundant, i.e. each subset of them
can be generated by linear combinations of the others (Daubechies et
al. 1986). Although in such cases the reconstruction is not exact
anymore, such a decomposition has a remarkable advantage when considering
de-noising applications (Daubechies 1990).
is highly redundant, i.e. each subset of them
can be generated by linear combinations of the others (Daubechies et
al. 1986). Although in such cases the reconstruction is not exact
anymore, such a decomposition has a remarkable advantage when considering
de-noising applications (Daubechies 1990).
The particular class of non-orthogonal 1-D wavelets and the corresponding
discrete wavelet transform together with the numerical algorithm we have
used was proposed by Mallat & Zhong (1992, see their Appendix
A). The multi-level decomposition described in Sect. 3.2 (click here) is a direct
application of wavelet-packets using this particular kind of base functions.


Up: Noise reduction in
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr