

Up: Image restoration by
In order to compare the results of deconvolution and the computational
efficiency of the original Richardson-Lucy algorithm with the adaptive scheme
tests for one- and two-dimensional profiles have been carried out. As the
measure of quality of the deconvolved profile, the Kullback-Leibler distances
(Titterington 1985) were used.
The first one describes the agreement between
the original profile before convolution and the estimate obtained from the
iterative procedure. The second one describes the discrepancy between the
convolved and noisy
input image and that obtained by PSF convolution of the
resultant profile.
The Kullback-Leibler distance (KL distance) is very
appropriate in this case as it is fully consistent with the ML principle. If two
compared profiles are identical, the likelihood achieves its maximum value, thus
the actual likelihood for differing profiles can be subtracted from this value.
In such a way, the KL distance is always positive and it tends toward zero if
the agreement between the compared profiles increases. At iteration stage r the
two KL distances are computed according to the following equations:

As the first test, the deconvolution of a one-dimensional double Dirac
profile convolved with a Gaussian profile with FWHM of 10 pixels and distorted
by noise has been carried out. The distance between the Dirac tips
was 6 pixels. The expectation value of background level was constant over the whole profile
and equal to 100 counts. Figure 1 (click here) presents the original twin Dirac profile and
its PSF convolved image degraded by Poissonian noise.
The profiles obtained by
the original iterative scheme and its adaptive modification after 500 iterations
are also presented. The advantage of the adaptive approach is fully evident. Not
only the resolution is substantially increased but also the background noise is
highly suppressed compared with the original algorithm which creates noticeable
artefact (appearing as a "wavy" structure).
This artefact is a one-dimensional
version of the ringing structure present in a two-dimensional deconvolved
image of a stellar profile. Figure 2 (click here) shows the KL distances for this test
example.
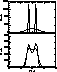
Figure 1: Deconvolution of the double Dirac profile. Top panel-original profile
and its image convolved with PSF and degraded by Poissonian noise.
Bottom panel-deconvolved profile
obtained using the Richardson-Lucy algorithm after 500 iterations (thick
line) and that obtained by its adaptive version (thin line)
As has been previously reported by Lucy (1994), the computational
efficiency of the original Richardson-Lucy scheme is satisfactory only for a few
tens of iterations and then it quickly vanishes. On the contrary, for the
modified algorithm, the efficiency retains a relatively high value. This means
that for the adaptive approach the number of iterations may increase without any
loss of the computational efficiency. Due to an additional penalization
constraining on the ML solution by the adaptive algorithm, the KL distance
H tends to a small positive value (not to zero) and, additionally, does so more
slowly than in the original scheme (see Fig. 2 (click here) bottom panel).
As a two-dimensional example of image restoration the deconvolution of a
double star image has been performed. Figure 3 (click here) presents the original image of a
couple of pixels each having 20.000 counts imposed on the background of constant
expectation value of 100 counts.
The PSF profile comes from the real CCD
observed stellar profile. The figure shows the image of a synthesized double
star degraded by Poissonian noise and its deconvolved images after 100
iterations.
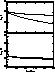
Figure 2: Kullback-Leibler distances for profiles from Fig. 1 (click here) as
functions of the number of iterations. Top panel-the distance between the
deconvolved and original profile. Bottom panel-the distance between the input
image and that obtained by convolving the restored profile with the PSF. Thick
line-Richardson-Lucy algorithm, thin line-adaptive
version
KL distances are displayed in Fig. 4 (click here). The quality of restoration can
be characterized by the total signal for the two central pixels of the
deconvolved double star. For the original Richardson-Lucy iterative scheme 68%
and for the modified algorithm 75% of the total energy is concentrated in these
two pixels. Moreover, the background noise, which is amplified by the original
algorithm, is fully suppressed by the adaptive one. For the original
Richardson-Lucy iterative scheme the KL distance h decreases to its minimum at
40 iterations, whereas for the modified algorithm it continuously decreases.
This means that the original approach achieves its maximum computational
efficiency after 40 iterations and subsequent iterations do not substantially
improve the resultant profile. The adaptive scheme, on the contrary, retains
its efficiency for an increasing number of iterations promising better image
restoration.


Up: Image restoration by
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr


