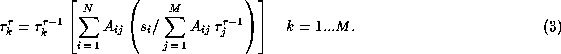
The condition of maximization of the likelihood function (see Eq. (2)) leads
to the commonly known iterative algorithm (Richardson 1972 and Lucy 1974):
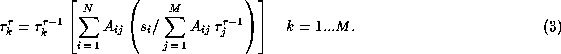
This iterative scheme preserves the sum of the retrieved parameters 
at each
stage of the procedure and starting from the constant profile 
(where 
)
converges to the stable solution of the ML problem.
For astronomical images obtained with multi-channel receivers (like CCD's) real objects are situated on a commonly appearing background produced, for example, by night sky illumination. Although the incoming photons have Poissonian statistics, after their conversion into measured counts-per-pixel and the consecutive stages of image treatment (e.g. bias, dark current and flat-field reductions) the initial statistics is transformed. Unfortunately, the way in which this transformation is carried out is strongly dependent on so many different factors that it is hard to predict the statistics of the output signal. The problem of image restoration based on generalized stochastic models of the signal has been addressed by some researchers (e.g.: Snyder et al. 1993; Snyder et al. 1994).
Of course some Poissonian-like dependence between the local noise and
the local signal should exist in the resultant image. If the local signal
increases both the local noise and the local S/N (signal to noise ratio)
increase. Equation (1) ought to be rewritten taking into account the image
background.
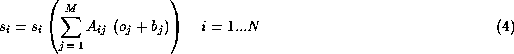
where the 
represent the true object and the 
are the background. Equation
(4) is valid for the case when the PSF is produced by telescope optics and
receiver.
As has been mentioned in the previous section, for an excessive number
of iterations the noise existing in observational data is amplified. This is
connected with the structure of Eq. (3). For image fragments where only noisy
background exists, the ratio ofobserved data 
and convolved parameters 
obtained at the iteration step r-1 may attain an excessively high or low value
and may be strongly unstable. After convolution with the transposed PSF (i.e.
correlation) these values are indeed smoothed out but can be transferred to
image fragments occupied by crucial objects, distorting the results of
deconvolution. In this way, the image noise is amplified and serious artefacts
appear. Thus, the restored image may substantially differ from the original one.
If the local S/N ratio increases, which occurs for objects substantially
exceeding the background noise, the iterative procedure weakly amplifies the
noise. The probability of the appearance of artefacts decreases and the restored
image is close to the original one.
This suggests a simple but quite 
approach to the problem of
stabilizing the iterative scheme for an increasing number of iterations. This
number should be subjected to the local S/N ratio. A similar approach,
connecting the local number of Richardson-Lucy iterations with the local
smoothness of structures in the image, has been previously elaborated by
White (1993).
For image regions with only a noisy background, very few iterations should be performed, whereas for objects with a relatively high S/N ratio, the number of iterations should increase to the maximum value asserted by the operator.
The main steps of the proposed algorithm follow. For the whole image the
first iteration is performed according to Eq. (3) beginning from a constant
profile 
. This iteration has a special meaning because it produces the
correlation of the input profile with the PSF:
For a symmetric PSF this correlation is identical with optimal filtering. For
an asymmetric PSF assuming a noiseless case we have:
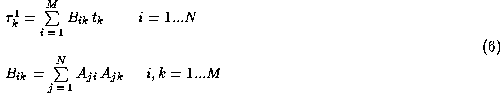
where B is a symmetric matrix. As can be seen, the result of the first iteration
is a convolution of the original unblurred image with a symmetric profile
substantially broader than the original PSF.
If one takes into account that, in general, resolution in the restored
image (for the appropriate criterion see Lucy 1992) increases with an increasing
number of iterations the dependence between the local number of iterations and
the local signal should not be a smoothly and slowly increasing function, if
resolution for regions of different signals is to be constant. It should rather
be a switch between the minimum number of iterations for image regions of very
low S/N and the maximum number of iterations for image regions of S/N exceeding
some limit. On the other hand, this dependence should not be as discontinuous
as the Heaviside step-function, if proper work of the iterative scheme is
desired. A sigmoid function commonly used in neural networks computations has
been chosen by the author. It may be treated as a smooth realization of the
Heaviside step-function. The ratio of the local signal to the local background
noise has been chosen as the independent variable.
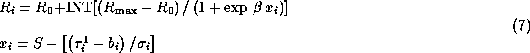
where 
, 
and 
are, respectively, the actual, initial (equal to 1) and
maximum (settled by the operator) number of iterations, 
are the local
background and 
are the background noise. The dimensionless parameter S
defines the value of signal to noise ratio for which the inflection of the
sigmoid function occurs. The parameter 
controls the slope of the sigmoid
function. These two parameters should be set in such a way that for 
of the order of background noise the number of iterations is close to 
and
for 
substantially greater (e.g. 10 times) than the background noise,
the number of iterations attains 
. The symbol INT denotes a function which
gives an integer number nearest to the actual value of the real variable. Use of
Eq. (7) requires the knowledge of local background 
and the level of its noise.
If the underlying background is relatively smooth, it may be estimated by a
smooth surface characterized by a restricted number of parameters. In such
cases, the two-output-channel Richardson-Lucy method may be used. It puts one
constraint on the solution for regions with data that can be fitted by a smooth
surface and another constraint for the remaining regions (White 1993). In many
cases it produces better results than the original Richardson-Lucy method.
After computing the maximum number of iterations for each image point
the Richardson-Lucy iterations described by Eq. (3) may begin. However, an
additional constraint is placed on the result of each iteration (including the
first one). The image values, less than the background level 
are set equal to
this level. This data clipping introduces some bias but its value is not
photometrically significant because of substantial filtering given by the first
step of the iterative procedure (see Eqs. (5) or (6)). Since the iterative scheme
modified in such a way does not conserve the sum of the image signal, a
further renormalization of the image is required. After renormalization, some
values may be once again less than the background level, so a consecutive
data clipping and image renormalization should be repeated. This iterative
procedure is continued until the actual sum of image signals is sufficiently
close to T. If the desired limiting discrepancy is of the order of a
millimagnitude, only a couple of iterations ought to be carried out with
CPU time consumption many times smaller than for one iteration of the
deconvolution procedure. The renormalization scheme described above may destroy
the local flux conservation by some nonlinearity of the photometric behaviour of
this algorithm. However, if the expectation value of the local background is
properly established the photometric error produced by this algorithm is fully
negligible.
If the actual number of Richardson-Lucy iterations r is greater than 
for a given pixel, the ratio of observed signal 
and convolved profile 
obtained at the previous iteration step is arbitrarily set equal to 1.0, which
means that for this pixel, full agreement between observed value and the PSF
convolution of the resultant profile has been achieved. Then, the convolution
with transposed PSF is made, but for pixels for which 
, 
is set equal
to 
. Richardson-Lucy iterations are carried out until r is equal to the
maximum 
over the whole image.
This modified iterative scheme has the property of an adaptive
behaviour. If the local signal is close to the background level, only very few
(or even one) iterations are carried out and the resultant profile is as smooth
as the input profile (or even substantially smoother). In this case the
resolution is highly suppressed but for low S/N ratio any attempt to perform a
"strong" deconvolution using any known method leads to spurious results. On the
other hand, if the difference between a local signal and background level is
really greater than the background noise, the local maximum number of iterations
rapidly increases to 
and resolution achieves its maximum level (expected
for this case). What is more, the quality of the images restored with the
adaptive algorithm for objects with large S/N ratio should be better than using
the original scheme. It follows presented earlier in this section. An
exceptional advantage of this scheme should be attained for original objects
with linear dimensions less than those of PSF, which is connected with a
relatively weak penalization of the solution. The advantage of the presented
method over the basic Richardson-Lucy method is mainly due to its adaptivity.
Whereas the original Richardson-Lucy algorithm converges attaining maximum
likelihood, the adaptive version converges attaining a value of likelihood which
is somewhat lower (due to additional constrains placed on the solution) but,
still very close to its maximum value.
An additional benefit of this approach is a remarkable reduction of the
mean number of iterations per pixel. Indeed, for pixels where the actual r is
less than 
, convolution of 
with PSF and convolution of the resultant
set of the ratios with transposed PSF are replaced by substitutions of
appropriate values. Furthermore, due to its simplicity, the adaptive scheme
should be relatively quick (less CPU time consuming) in comparison with the
other, more complex approaches to the image restoration problem that have
been proposed (Piña & Puetter 1993; Starck & Murtagh 1994; Terebizh
& Biryukow
1994).