One could assert that the newly proposed iterative algorithm, in some aspects
established 
, especially in the introduction of data clipping has
photometric
Figure 3: Deconvolution of the double star profile (logarithmic
grey scale). Panel a) original profile as a couple of pixels,
b) observationally obtained PSF profile, c) synthesized double star blurred
by Poissonian noise, d) image deconvolved by the Richardson-Lucy scheme after
100 iterations, e) profile restored using the adaptive algorithm
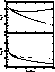
Figure 4: KL distances for deconvolved images of the double star profile from
Fig. 3 (click here) as functions of the number of iterations. For detailed description see
Fig. 2 (click here)
properties poorer than the original Richardson-Lucy algorithm.
As a comparative test of photometric fidelity of both the deconvolution methods
aperture photometry of synthetic stellar cluster has been undertaken. Two
hundred stellar images having Gaussian profile of the radius at half-maximum
equal to 2.0 pixel have been randomly distributed in the frame with a spatial
concentration increasing toward the cluster centre. At least half of the
stellar images were overlapping each other. Total counts contained in the
stellar profile (stellar brightnesses) have been randomly distributed in the
range of about 6 mag. The background was 16 counts. Seven different Poissonian
noise realisations have been made for the basic frame. Each noisy frame has
been restored using 250 iterations of both the methods. For the adaptive
iterative scheme the gain in computational speed was 1.7 times. Then the
aperture photometry with diaphragm radius of 2.0 pixel was carried out.
Additionally, the astrometry using the stellar brightness centre was performed.
As a measure of photometric fidelity the magnitude differences between the
results of stellar aperture photometry and the original stellar brightnesses has
been chosen. Figure 5 (click here) presents these differences (
) as the mean values in
the set of seven different noise realisations. Generally, adaptive deconvolution
has photometric properties markedly better than the Richardson-Lucy algorithm
for which the ringing effect in connection with restoration artefacts produce
distinct systematic errors. Astrometric properties of both algorithms are almost
equally excellent. Mean deviations between original positions of stellar images
and those obtained from restored frames are in both X and Y directions less
than 0.2 pixel.
The results of the tests presented in the previous section and the comparison of photometric properties indicate the predominance of the newly elaborated adaptive approach over the basic algorithm, especially in the case of original objects with linear dimensions of the order of the FWHM of the PSF or less.
Figure 5: Residuals between the magnitudes obtained from the aperture photometry
of the restored frames and the original magnitudes of stars in the stellar
cluster as a function of the original counts in stellar profile. Top panel-
adaptive algorithm, bottom panel-Richardson-Lucy algorithm. Vertical bars
represent standard deviations derived from the set of seven different noise
realisations. Mean values of the residuals are at the centres of these bars
Thus, the adaptive algorithm should be an excellent tool in restorations of crowded star fields enabling their precise photometry and astrometry. Its use for restoration of extended sources should always give some advantages in computational efficiency and quality of results over the original Richardson-Lucy scheme. As has recently been shown by Busko (1994), the Richardson-Lucy method is one of the most effective and accurate among deconvolution algorithms including the Maximum Entropy, CLEAN and Fourier-Wiener filtering. This means that any attempt of improving the basic algorithm is of great worth.