We have two possibilities to derive the slope of the IMF. First, we can use the isochrone which was found to fit best to the CMD to convert the apparent magnitudes of the main sequence stars to masses. This method has been used in our recent papers (Will et al. 1995a,b; Vázquez et al. 1995) and proved to be very successful. Since we are dealing with hot stars and we do have observations in the U passband, we can also use the transformation equations of Massey et al. (1995b) to transform our CMD to a HRD. This enables us to overplot tracks from stellar evolutionary models and to count stars in certain mass intervals. Both methods will be used here and their results will be compared.
We did not apply any completeness correction (similar to
e.g. Oey & Massey (1995) but in contrast to e.g. Will et al. 1995a,b).
Our photometry of N44 is so deep
(see Figs. 2 (click here) and 7 (click here)) that we
expect a high contamination of LMC field stars in the faint star regime.
But, since we do not have any observations of a comparison field to perform
a statistical field star subtraction,
the faint star regime would, even with a completeness correction,
be useless for us.
The luminosity function (Fig. 12 (click here)) suggests that our photometry
is complete down to 
mag (i.e. 
mag),
corresponding to 
or 
.
The 5 Myr isochrone was used to derive a relation between the absolute
magnitude 
and the mass of all stars on the main sequence
(same criteria as for the luminosity function).
The stars were binned in intervals of 0.1 in log mass.
We assume a power law form of the IMF for the restricted mass range under
investigation and use the equation
where x is the slope of the mass function.
In this notation the value for the slope of the IMF in the solar vicinity
is x=1.35 (Salpeter 1955).
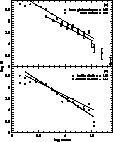
Figure 13: Initial mass function (IMF) for LH47/48.
a) Comparison of the IMF as derived from BV photometry
(filled symbols, solid line)
and from the HRD (open symbols, dotted line).
b) Comparison of the IMF of inside
(filled circles, solid line) and outside (open circles, dotted line)
the shell of N44.
In both plots the slopes of weighted linear regressions are given
Figure 13 (click here) shows the result.
In Fig. 13 (click here)a the star counts for the entire field of view are
plotted vs. the logarithm of the mass.
error bars are also plotted.
In the mass range from 
(
) to 
(
) the assumption of a power law seems reasonable.
The lower limit fits well with the incompleteness limit derived from
the luminosity function.
A weighted linear regression in the mentioned mass range gives a slope
of the mass function of 
.
The solid line in Fig. 13 (click here)a shows this fit.
The luminosity function implied a difference between the stellar populations
inside and outside of the superbubble N44A (see Fig. 12 (click here)b).
We used the same selection criteria as for the luminosity function
(inside: all stars in a circle with a radius of 
;
outside: all stars outside a circle of radius 
)
to investigate this for the IMF.
Figure 13 (click here)b shows the star counts for both regions.
The filled symbols show the mass function for the interior of the shell.
A weighted linear regression for the same mass range as mentioned above
gives a slope of 
(solid line).
The open circles give the result for the exterior region
where we find a slope of the IMF of 
(dotted line).
We used a plot similar to the one shown in Fig. 10 (click here) (left panel)
to count the stars between the stellar evolutionary tracks on the main sequence
band of the HRD.
The blue stars leftwards of the main sequence are scattered into this region
due to uncertain photometry and thus have been omitted for the counting.
The red stars to the left of the main sequence near 10 
have been
excluded.
However, since we want to compare our results with those obtained
by Oey & Massey (1995), we did count all evolved stars which are more massive
than 12 
.
The star counts between the tracks have been normalized to the same bin
size (0.1 in log mass) than those from the photometry and have been
plotted in Fig. 13 (click here)a (open circles).
The error bars are 
errors.
The IMF derived in this way lies clearly below the one from the photometry.
This is a direct influence of the fact that for a placement in the HRD
a star has to be detected in all three passbands U, B and V.
In the U passband our observations are not very deep and incomplete
already on the upper main sequence.
However, the slope of 
derived for the mass range below
the turn off point of the main sequence is quite similar to that from
the BV photometry.
We recognize a clear upturn of the IMF slope for stars more massive than
20 
(0.1 in log 
).
For the mass range from 12 to 85 
we find a slope of x = 2.1.
We found very similar slopes for the IMF from both methods described above. This is somewhat surprising because of the lower number of stars in the HRD compared to the BV CMD. Using the HRD offers the possibility to count stars up to much higher masses than the turn off point of the best fitting isochrone. This leads to a steeper mass function slope since some stars may have already vanished and are thus not counted, although they were created together with the stellar population which is still observed. The problem has already been discussed by Will et al. (1995b) for the LMC OB association LH58. Values derived by this method should therefore be treated with care.
Oey & Massey (1995) give an IMF slope of 
(
in their notation) for the association.
This value was derived by the second method described above, i.e.
counting the stars between the tracks in the HRD.
It fits well to the results derived from both methods in this paper.
Oey & Massey (1995) do not find a significant difference between the IMF slopes
inside and outside the shell.
We find a change of x from 1.2 inside to 1.5 outside the shell,
i.e. we find relatively less massive stars
outside the shell than inside where the association LH47 is located.
This is the opposite direction of IMF slope difference reported by
Parker et al. (1992) for LH9 and LH10, the associations inside and
on the rim of the superbubble N11.
There more massive stars seem to have formed in the association which is
located on the rim of the superbubble.
The overall IMF slope found for LH47 fits well within recent derived IMF slopes in the LMC as well as in our galaxy. Will et al. (1995b) found x = 1.2 for LH58 in the LMC. For that association Garmany et al. (1994) found x = 1.6, which was updated to x = 1.4 in Massey et al. (1995b). The later paper also compiled other IMF studies of OB associations in the Magellanic Clouds and of open clusters and associations in our galaxy (their Table 5). The Magellanic Cloud associations show IMF slopes in the range from x = 1.1 to 1.6. In the case of the galactic clusters/associations the range is larger, from x = 0.9 up to x = 2.1. Other IMF studies of globular clusters and galactic clusters have been discussed in Will et al. (1995a,b) and Hill et al. (1994).
There is a clear tendency to find IMF slopes near the Salpeter (1955) value. This strongly supports the idea of an universal shape of the IMF. We think that the differences found between the stellar aggregates are more due to scatter (especially at the massive end of the IMF), quality of the observations (i.e. completeness), and the analyzing methods (i.e. counting of stars in CMD or HRD) than due to real differences of the IMF of the objects under investigation. For a comparison of studies which analyze different mass ranges one should also keep in mind that the representation of the IMF with a power law is only valid for a narrow mass range. For larger ranges, i.e. for mass ranges of more than one order of magnitude, the Miller & Scalo (1979) law should be applied.