We have used the code developed by R. Van de Weygaert (1991, 1994, see also Goldwirth et al. 1995) in order to construct Voronoi tessellations. Although the code has been developed to allow for much more sophisticated cases, we limit ourselves to the simplest case where a given number of points is distributed in walls or filaments of a given thickness. To mimic noise we have added an Poisson distribution of particles in the whole box.
Using the same nuclei of the Voronoi tessellation, the filaments (defined as the edges of the walls) would have approximately the same separation as the walls (contrary to what we expect in nature). Therefore, we did not combine a filamentary structure with a wall-like structure in one realization, but made a second realization for filaments alone. Note also that the filaments of a Voronoi tessellation are not distributed like filaments of real galaxies. Nevertheless the points of these Voronoi tessellation form one-dimensional structure elements with a priori known properties which should be recovered by the core sampling method.
The mean diameter of the Voronoi cells and the size of the box are
free input parameters of the code. For the core-sampling analysis it
is only important that the mean number of structure elements along a
random line crossing the box be large enough. We have chosen 6 cells
and 20 cells for the analysis of walls and filaments,
respectively. The analysis itself can be performed in units of the box
length. For the graphical representation we have chosen formally a box
size of 300 Mpc. We have chosen 200 000 and 400 000 points to represent
the walls and the filaments, respectively. Due to the formal
definition of the box size these numbers are not directly comparable
with the number of galaxies in the corresponding volume. However, in
that case the mean number density of points is of the order 
, i.e of the same order as the galaxy density. Also the the
mean separation of structure elements is of the same order as found
for galaxies, so that we can indeed draw conclusions from our test to
the situation found in observational surveys. The noise level chosen
(50% for walls and 25% for filaments) is in these realisations an
approximate upper limit for which the known properties can be
recovered with high accuracy.
For the first test, we chose a mean size of the cells of 50 Mpc.
Our first realization consists of 
randomly distributed cells in box
of 300 Mpc length. 200 000 points are distributed only in walls
around the cells. We chose a Gaussian density profile of the
walls with a thickness of 2 Mpc. On the left hand side of
Fig. 1 (click here), a slice of 8 Mpc thickness of this realization is
shown. In order to test the stability of the core-sampling method, we
made a second realization with 100 000 additional points which were
randomly distributed (Fig. 1 (click here), right).
As explained in Sect. 2.1, the starting point of the core-sampling analysis is the construction of randomly distributed cylinders in the simulation. For illustration, we put four of these cylinders into each of the slices shown in Fig. 1 (click here). The diameter of the cylinders is equal to the thickness of the slice (8 Mpc). In the lower part of the figures, the distribution of points in these cylinders is plotted vs. the radius of the cylinder. This radius will be used in the following as one diagnostic parameter as described in Sect. 2. Indeed, for sheet-like structures like the walls in our Voronoi tessellations, the mean number of clusters in the 1D cluster analysis is independent of the core radius. One can clearly see from Fig. 1 (click here) that in both cases almost all walls will be identified as walls.
Next, all particles 
in a given cylinder of radius 
are
projected onto the axis of the cylinder. From Fig. 1 (click here) it
is clear that there is also noise besides real structures in the
resulting one-dimensional point distribution. The degree of noise
depends on the chosen parameters of the generated sheets and on the
parameters of the core. The noise particles in underdense regions can
be removed using the reduction procedure described in Sect. 2.1. The
reduced sample at which the further analysis will be performed is
characterized by three parameters: the fraction f, the threshold
, and the core radius 
.
Further, we use the iterative fitting procedure described in Sect. 2.2
to find the best fit to Eq. (1 (click here)). According to our assumption,
the resulting clusters must be Poisson distributed for the some range
of linking length. However, this assumption must be tested for the
samples under consideration. As an example we show in
Fig. 2 (click here) the fit to Eq. (1 (click here)) for four sets of
parameters (f=1, 0.5, 
, 2 Mpc and 
:
left for walls and right for walls with randomly distributed points).
Using Eqs. (5 (click here)) and (6 (click here)), where 
is the diagnostic
parameter, we determine now the surface density of filaments and the
linear density of walls for each pair of parameters f and
. This procedure is illustrated by Fig. 3 (click here). for
four pairs of parameters. (Note that each curve of
Fig. 2 (click here) corresponds to one point in Fig. 3 (click here)).
From Fig. 3 (click here) we extract the linear density of walls as the
zero point of the curve and the surface density of filaments as the
gradient. The fits to Eqs. (5 (click here)) and (6 (click here)) were performed
over 9 equally spaced values of 
in the interval 
.
As the final result of the analysis, we present in
Fig. 4 (click here) the mean distance of the walls 
and in Fig. 5 (click here) the surface density of
filaments 
depending on the threshold 
. (Note,
that each curve of Fig. 3 (click here) provides one point in
Fig. 4 (click here) and one point in Fig. 5 (click here).) The final
values of 
and 
are listed in Table 1 (click here).
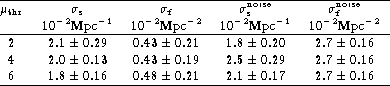
Table 1:
Test of the wall distribution
The noise of apparent filaments is an objective characteristic of the
sample under consideration. The population of filaments dominates for
all thresholds 
that resemble the small density contrast in
the walls, since the number of particles concentrated into sheets
exceeds the noise particles only by a factor of two. In this respect
our synthetic models differ from the Las Campanas Redshift Survey,
where for high threshold multiplicity the filament population had
disappeared, and only the richest sheet-like elements survived.
As a second test we have investigated a pure filamentary structure and filaments superimposed by randomly distributed particles. To this end we have constructed a Voronoi tessellation with 400 000 particles which are distributed at the edges of the cells, and a second one with an additional 100 000 randomly distributed particles. For this test we chose a mean size of the cells of 15 Mpc. In Fig. 6 (click here) we show a slice of 4 Mpc thickness and four cores of radius 2 Mpc. Further steps in the analysis are as above. We made two realisations of Voronoi tessellations containing only filamentary structure: In the first realisation we chose a radius of filaments of 0.2 Mpc, in the second 0.1 Mpc.
For these synthetic models, we omit the figures corresponding to
Figs. 2 (click here)-3 (click here), but present only the final results,
i.e. the density of walls 
and filaments
vs. 
for two thresholds 
and the two different radii of filaments. (see
Figs. 7 (click here)-8 (click here)). The final structure parameters
are given in Table 2 (click here).
Let us note that in this case the mean edge separation along a random
straight line is not identical to the mean size of the cell but is of
the order of the mean length of the filaments. The mean distance of
particles along the filaments in our sample is of the order of 1 Mpc.
Therefore, we expect that the set of particles forms a broken network
structure which can be characterized by the surface density of
filaments 
. With a higher mean density we could create
also a complete network structure which, however, in reality does not
exist.
Since all filaments were created using the same procedure their
parameters can vary only statistically. We can use Eq. (7 (click here)) to
determine 
as is shown in Fig. 8 (click here) (dashed
line). In case of 
the points corresponding to a large
fraction f do not follow the line predicted by Eq. (7 (click here)).
Rejecting these points, a linear fit would predict a somewhat smaller
. We expect this result, because we are now measuring only
the rare high-density filaments.
The noise strongly increases the full surface density of filaments
(Fig. 8 (click here), right). The rejection of
(
) of particles depresses the noise impact and leads us back to
noiseless data. Since most or all observed galaxies are incorporated
into structure elements the noise impact is not expected to be severe
in catalogues. Following the rejection procedure we can obtain for
all realizations the same result 
which
corresponds to 13.6 Mpc mean separation (see Fig. 8 (click here)).
Figure 6 (click here) (bottom) indicates that some of the filaments masquerade as sheets. We have discussed this problem already in Sect. 2.4. In this case the error bars strongly increase as a result of the sparse sample statistics of elements which the core-sampling method wrongly detects as sheets (see Fig. 7 (click here)).
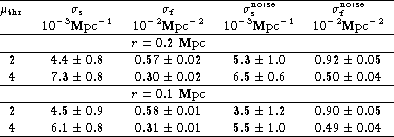
Table 2:
Test of the filament distribution