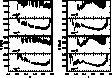The first deep galaxy surveys which have become available have shown that the galaxies are not at all homogeneously distributed on large scales. Large voids, small filaments, massive clusters, and walls of galaxies can be observed. How these structures have evolved from the initially nearly homogeneous universe is one of the central problems in modern cosmology. Many theoretical models of structure formation have been suggested. Powerful mathematical statistical methods are necessary in order to describe this structure, to obtain its quantitative characteristics, to compare the theoretical models and simulations with observational catalogues, and, eventually, to find the correct theory of structure formation.
The standard approach for testing models is to define a point process which can be characterized by statistical methods. This could be the distribution of galaxies of a specific type in deep surveys or clusters of galaxies. In order to compare models of structure formation, the different distribution of dark matter particles in N-body simulations could be tested as well.
The most widely used statistics are the n-point correlation functions, the counts-in-cells method, and the void probability function. The geometrical and topological properties of the point distribution can be investigated by the percolation technique (Zeldovich et al. 1982), the minimal spanning tree (Barrow et al. 1985), the genus of the smoothed density field (Gott et al. 1986, 1989), and the Minkowski functionals (Mecke et al. 1994).
All these different statistics measure the global properties of a point process. However, when looking at a point process we also see different structures. The morphology of these structures is an important property of the point distribution. (Note also the warning of Barrow & Bhavsar (1987) that we tend to see by eye structures which do not exist). Therefore, it is important to develop statistics which distinguish between different structure elements in a point distribution and find their typical scales (if any exists).
Figure 1: Top: a slice of 8 Mpc thickness, bottom: radial particle
distribution in the four cylinders shown at the top part of the figure
(the dashed line indicates the minimum core radius used in the
analysis), left: only walls, right: walls with a background of
randomly distributed particles
Figure 2: A fit to the equation 
(left:
only walls, right: with a background)
Figure 3: A fit to the Eqs. (5) and (6) from which 
(dots) and
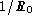(triangles)
are obtained, (left: only walls, right: with a background)
Figure 4: Mean separation of walls for three multiplicity thresholds (left:
only walls, right: with background particles)
Figure 5: Mean surface density of apparent filaments for three multiplicity
thresholds (left: only walls, right: with background particles)
Figure 6: Top: a slice of 4 Mpc thickness, bottom: radial particle
distribution in the four cylinders shown at the top part of the figure
(the dashed line indicates the minimum core radius used in the
analysis), left: only filaments, right: filaments with a background of
randomly distributed particles
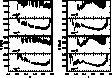
Figure 7: Mean separation of apparent walls for two multiplicity
thresholds (top: radius of filaments 0.2 Mpc, bottom: radius of
filaments 0.1 Mpc, left: only filaments, right: with background
particles)
Figure 8: Mean surface density of filaments for two multiplicity
thresholds (top: radius of filaments 0.2 Mpc, bottom: radius of
filaments 0.1 Mpc, left: only filaments, right: with background
particles)
In this direction a first attempt was made by Vishniac (1986). He used the moments of a point distribution in a window to measure the amount of filaments in two-dimensional galaxy distributions. Recently, this method was generalized to three-dimensional point distributions (Luo & Vishniac 1995). Both the number of filaments and walls and typical scales of the structure can be found. Minkowski functionals are also efficient discriminators for idealized one-, two- or three-dimensional structure elements (Schmalzing et al. 1996). However, using Minkowski functionals it is difficult to extract such structure elements from a superposition of all possible elements including Poisson noise.
Using the core-sampling method (Buryak et al. 1991; Buryak et al. 1994) one can find structure elements and their typical separation. The method was designed to find one-dimensional filaments and two-dimensional walls within observational surveys of galaxies (Buryak et al. 1994; Doroshkevich et al. 1996) and in simulated samples (Doroshkevich et al. 1997). Here we want to apply the method to an idealized model mimicking many features of the observed patterns in the galaxy distribution. The model employed here is based on the concept of a Voronoi tessellation (Goldwirth et al. 1995). Such a test allows us to compare the input and output structure parameters and, thus, to test how powerfully this method can discriminate structure elements, determine their distribution and typical parameters.
The basic idea of the core-sampling method is to reduce the analysis
of a three-dimensional galaxy distribution to the investigation of the
distribution of structure elements along random straight lines (the
"core"). Such an approach allows us to avoid any discussions and
descriptions of the very complicated multiconnected structure as a
whole as well as any conventional definition of a "structure element"
and "void" in the three-dimensional space. The core-sampling method
has to deal only with a one-dimensional point distribution. It allows
us to define two typical populations of structure elements, namely,
filaments and sheets, and provides us with two objective
characteristics of the spatial distribution of these elements, namely
the surface density of filaments and the linear density of sheets.
The surface density of filaments 
is simply the mean number
of filaments intersecting a unit area of arbitrary orientation, while
the linear density of sheets 
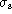is simply the mean number
density of sheets crossing an arbitrary straight line. These
characteristics provide a local description of a random
three-dimensional network structure. In Sect. 2 we will briefly
outline the general properties of this method
The three-dimensional Voronoi tessellation consists of a number of Voronoi cells enclosed by the planes bisecting the lines between the nuclei of neighbouring cells (van de Weygaert 1991). The intersections of these planes are lines and points. Therefore, the three-dimensional Voronoi tessellations consists of three structure elements: the walls around the voids, the edges (intersection of walls) and the nodes. Within the three-dimensional Voronoi tessellation particles may be distributed on each of these structure elements or distributed around them according to a given distribution function. Moreover, the Voronoi tessellation can be superimposed by randomly distributed particles. Thus it is a unique tool for testing algorithms purporting to describe the structure elements of a point distribution.
In Sect. 3 we will briefly describe Voronoi tessellations and the creation of synthetic samples. We apply the core-sampling method to these synthetic samples and compare the results with the input structure element. We discuss the accordance between the expected and found structure parameters and conclude that the core-sampling method is a powerful tool to investigate the distribution of structure elements.