We consider in this section the adaptation of the Hipparcos data processing to the
case of short period astrometric binaries, in particular when the hippacentre and
the photocentre are not alike. In this case, the reduction consists of
producing the astrometry of the centre of mass and of determining
the hippacentre path, yielding both 
and B. Otherwise, it yields only the
scale
of the photocentric orbit.
Let S be a program star of the
Hipparcos mission. The main goal of the standard astrometric processing was to
determine accurately the position of the star with respect to the centre of
mass C of the solar system. When S is a single star, the position vector
CS at epoch
t may be modelled with the usual five
astrometric parameters:
corresponding to the coordinates of position, the
parallax, and the two components of the proper motion. Although our treatment makes
use of the ecliptic reference frame, this choice is of no consequence in the
following.
In the case of a short
period binary, the instantaneous observation is tied to the hippacentre H and we
have,
where G is the centre of mass of the binary and H the hippacentre, which is the
same as the photocentre for very close binaries. The motion of G is well described
by the five astrometric parameters 
, while
is given by Eq. (7). If everything is known on the double star, 
can be computed at any time and the raw observations duly corrected for the
duplicity effect and subsequently solved for the astrometric parameters of the
centre of mass. If only the relative orbit is known, one must adjust in a single
process both the astrometric parameters of the centre of mass and the physical
parameters 
and B of the binary. For separation less than 
0
3, the method will fail as the hippacentre and the photocentre merge and only
could be determined.
The equations relating the observations to the astrometric and physical parameters
are all non-linear. An approximate value of the position, proper motion and parallax
can be used to linearize the set of equations in the vicinity of this values. No
particular problem arises in this step. As for the physical parameters 
and
B one must be much more careful, and in most case the plain linearization is not
sufficient and several tricks must be implemented to ensure the convergence during
the iterations, and that the solutions we arrived at satisfies the non-linear
system. With these safeguard we observed that the solution was not sensitive to the
quality of the initial values of
and B and that the non-linearity problem was overcome. The processing
consisted primarily in the resolution of an over-determined system of N
equations (the number of observations) with five or seven unknowns, by a weighted
least squares. The various steps are outlined in Fig. 6 (click here).
As the magnitude difference is generally fairly well known, the input value of 
is not totally arbitrary. Consequently, a first guess of B can also be based on
the mass luminosity relation for dwarf stars.
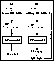
Figure 6: Schematic principle of the specific processing of the short period
binaries. In an ideal case a) where the intensity and mass fractions are perfectly
known, we just use this information to shift the observations to the centre of mass
and then solve for the astrometric parameters. Whenever it is not feasible
b) one uses a non linear model with 7 unknowns (5 astrometric parameters for the
centre of mass + 2 physical terms)